Vous êtes-vous déjà demandé en quoi les nombres rationnels diffèrent des autres nombres ? Dans cet article, nous explorerons en profondeur les nombres rationnels, y compris leurs caractéristiques uniques et leur classification. Préparez-vous à mieux comprendre le concept !
Que sont les nombres rationnels ?
Les nombres rationnels (ℚ) sont une sous-classe des nombres réels qui comprend tous les nombres pouvant être exprimés sous forme de fraction. Cela signifie que les nombres rationnels sont ceux qui peuvent être écrits comme un rapport de deux entiers, a/b, où b ≠ 0.
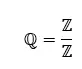
Les nombres rationnels peuvent également être exprimés sous forme de nombres décimaux répétés ou finis , car ils sont constitués d’une série de chiffres répétés. Quelques exemples de nombres rationnels sont 1/2, 3/4, 10/3, 2/3 et π (pi).
Sous-ensembles de rationnels
Les nombres rationnels peuvent être divisés en deux sous-ensembles :
- Les entiers , qui incluent 0, tous les nombres naturels et tous les nombres négatifs.
- Les nombres décimaux ou nombres fractionnaires , qui sont tous ceux qui expriment des valeurs formées par : une partie entière et une partie décimale, cette dernière permet d’exprimer des valeurs inférieures à l’unité.

Une autre sous-catégorie de l’ensemble des réels sont les nombres irrationnels , qui sont un peu plus complexes.
Exemples de nombres rationnels
Les nombres rationnels sont ceux qui peuvent être exprimés comme une fraction, c’est-à-dire comme un quotient de deux nombres entiers. Voici quelques exemples de nombres rationnels :
-23
-4/5
-1/2
-7/9
Toutes les fractions qui représentent un nombre entier sont également rationnelles. Par exemple:
-1/1
-2/2
-3/3
Propriétés des nombres rationnels
La principale caractéristique des nombres rationnels est qu’ils ont toujours un dénominateur non nul .
La deuxième propriété de cet ensemble est que chaque nombre rationnel peut être représenté par une infinité de fractions équivalentes . Par exemple, le nombre rationnel 3,5, qui est égal à 7/2, peut aussi s’écrire 14/4, 28/8…, et une infinité d’autres fractions.
Les nombres rationnels satisfont également la propriété distributive . Cela signifie que multiplier ou diviser une fraction par une autre n’affectera pas le résultat :
(a/b) (c/d) = (ac)/(bd)
(a/b)/(c/d) = (ad)/(bc)
Représentation des nombres rationnels
Les nombres rationnels peuvent être représentés de plusieurs façons, mais la plus courante est par une fraction . Une fraction est composée de deux nombres : le numérateur et le dénominateur.
Le numérateur indique combien de parties du tout sont considérées, tandis que le dénominateur indique combien de parties égales sont dans le tout. Par exemple, si un gâteau est divisé en huit tranches égales et que trois de ces tranches sont mangées, la fraction qui représente la quantité de gâteau mangé serait de 3/8.
Une autre façon de représenter les nombres rationnels est par des décimales . Les décimales sont une manière abrégée d’écrire une fraction où le dénominateur est un nombre 10, 100, 1000, etc. Par exemple, si vous avez 1/4 d’une tarte, cela peut être exprimé par 0,25 (ce qui signifie “0 entier et 25/100”).
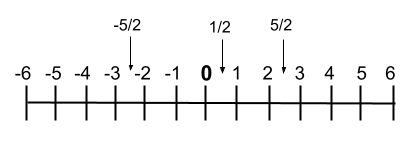
Bien que, si nous voulons les représenter graphiquement, nous pouvons également les écrire sur la droite numérique , dans laquelle l’ordre des nombres peut être très bien vu. Ensuite, nous vous montrons un exemple de cette ligne :
opérations rationnelles
Les opérations fondamentales des nombres rationnels sont les mêmes que celles des nombres entiers : addition, soustraction, multiplication et division. Si vous souhaitez apprendre à résoudre ce type d’opérations, nous vous recommandons de lire notre article sur les opérations avec des fractions .
Cependant, si vous travaillez sur des nombres rationnels avec une base décimale, vous devez suivre la procédure de résolution des opérations que vous utilisez lorsque vous traitez avec des valeurs décimales .
Conclusion sur l’ensemble des nombres rationnels
Après cette explication exhaustive, nous pouvons conclure que l’ensemble des nombres rationnels est l’un des plus importants en mathématiques. Il contient tous les nombres pouvant être représentés sous forme de fraction, ce qui nous permet d’exprimer très précisément des quantités.