Les nombres décimaux ont une grande importance dans le monde mathématique, mais savons-nous vraiment ce qu’ils sont et comment ils fonctionnent ? Dans cet article, nous allons tout vous expliquer.
Que sont les nombres décimaux ?
Les nombres décimaux sont des nombres non entiers (non englobés par l’ ensemble entier ), ayant une partie entière et une partie décimale. Cette partie décimale s’écrit après une virgule et permet d’exprimer des valeurs inférieures à l’unité.
Les nombres décimaux sont une façon de représenter les nombres fractionnaires . En effet, le concept de fraction est assez similaire à celui de valeur décimale. Nous pouvons le voir dans l’exemple suivant : 7/2 est égal à 3,5 . Ils maintiennent une équivalence numérique, seulement qu’ils sont écrits différemment.
Le nombre “3,5” est un nombre décimal qui se lit comme “trois virgule cinq”, sa partie entière est 3 et sa partie décimale est égale à 5. Puisque les nombres décimaux sont exprimés en utilisant le système de notation décimale, nous pouvons décomposer le nombre comme ceci :
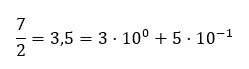
nomenclature décimale
Dans l’écriture de ces nombres, deux types de notation sont couramment utilisés : la notation standard (ou notation décimale) et la notation scientifique . Ce premier est le plus courant et c’est celui que nous avons utilisé jusqu’à présent.
Alors que la notation scientifique est une forme abrégée de la notation standard. En notation scientifique, un nombre décimal s’écrit comme un nombre entier multiplié par une puissance de 10 . Par exemple, la quantité 0,0054 peut être écrite en notation scientifique sous la forme 5,4 · 10 -3 .
Concernant l’écriture non numérique des décimales, on utilise une notation qui fait référence à la position qu’occupe chaque chiffre décimal. Eh bien, tout comme la partie entière a : l’unité, la dizaine, la centaine… La partie décimale a : le dixième, le centième, le millième…
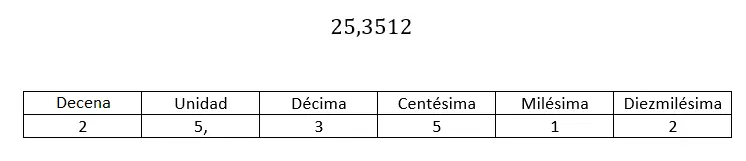
Ce qui marque le nom de chaque chiffre est la position qu’il occupe par rapport à la virgule . De cette façon, lorsque vous avez un nombre décimal et que vous voulez savoir quelle est la valeur du centième, vous devez regarder le deuxième chiffre (à partir de la virgule, vers la droite). Dans le cas ci-dessus, le centième est égal à 5.
types de décimales
Les nombres décimaux peuvent être classés comme suit :
- Décimal exact : possède un nombre déterminé et fini de décimales. Par exemple : 9 263.
- Décimal répétitif : a un nombre infini de décimales.
- Décimal répétitif pur : la partie décimale est constituée d’un nombre qui se répète à l’infini. Par exemple : 2.1515151515… Puisque 15 se répète indéfiniment.
- Décimal répétitif mixte : la partie décimale est composée d’une valeur, suivie d’un autre nombre qui se répète à l’infini. Par exemple : 2.4615151515… Puisque 46 ne se répète pas.
- Décimal non répétitif : a une partie décimale infinie, qui ne se répète pas. Dans cette section, nous trouvons quelquesconstantes mathématiques , la racine carrée de deux…

Propriétés des nombres décimaux
Les nombres décimaux ont plusieurs propriétés, notamment :
- Une décimale ne change pas si des zéros sont ajoutés à droite, donc le nombre 0,25 est équivalent à 0,250 et 0,2500. Fondamentalement, parce qu’ils expriment le même montant.
- Les décimales sont équivalentes à des fractions, par exemple, une demi-unité (1/2) est représentée par 0,5.
- Si nous multiplions ou divisons un nombre décimal par des puissances de dix, nous devons déplacer la virgule décimale : vers la droite si nous multiplions et vers la gauche si nous divisons.
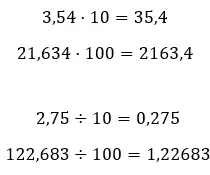
- Vous pouvez simplifier un nombre décimal, cela se fait en arrondissant les nombres décimaux . Cette méthode consiste à exprimer moins de chiffres décimaux, en modifiant au minimum la valeur du nombre. Si vous souhaitez apprendre à utiliser ce système de simplification, nous vous recommandons de saisir ce dernier lien.
Représentation des nombres décimaux
L’ensemble décimal peut être représenté sur la droite numérique comme tous les autres ensembles.
Partant du fait que les décimales ont une partie entière et une décimale (inférieure à l’unité), on peut en déduire que les décimales sont représentées entre les entiers . Par exemple, entre le nombre 0 et 1, on trouve des décimales infinies. Ci-dessous, vous pouvez le voir représenté dans la ligne :
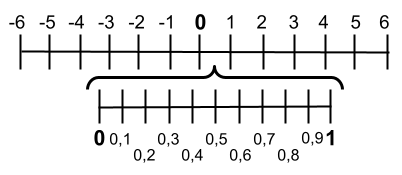
Comme vous pouvez le voir sur l’image, nous avons écrit les dix dixièmes entre 0 et 1. Bien qu’entre ces deux nombres il y ait des décimales infinies , des représentations très complexes peuvent être faites. Et de plus, cela ne se produit pas seulement entre 0 et 1, mais cela se produit entre tous les entiers.
Opérations sur les nombres décimaux
Les opérations des nombres décimaux sont similaires à celles des nombres entiers. La seule différence est que les positions des chiffres décimaux doivent être prises en compte. Par conséquent, avant de résoudre une opération, vous devez vous assurer que vous travaillez toujours avec les mêmes chiffres : dixièmes avec dixièmes, centièmes avec centièmes…
Ensuite, nous allons faire une brève revue des quatre opérations arithmétiques de base avec des décimales :
- Addition de décimales :

- Soustraction de nombres décimaux :

- Multiplication de décimales :

- Division de décimales :

Usages et applications des nombres décimaux
Les nombres décimaux sont très utilisés dans la vie quotidienne et en mathématiques. Par exemple, lorsque vous achetez quelque chose dans un magasin, vous devez connaître le prix de ce que vous achetez, et ce prix sera exprimé en nombres décimaux. En outre, ils sont utilisés pour mesurer des distances, des poids et d’autres aspects de la vie quotidienne.
En mathématiques, les nombres décimaux nous permettent d’exprimer facilement des quantités très petites ou très grandes. Et ils nous permettent également de faire des calculs avec une plus grande précision . Par exemple, si nous voulons calculer la moitié de 3 unités, nous pouvons la diviser en deux parties égales et obtenir 1,5 unités.