Matrice jacobienne et jacobienne

Sur cette page, vous trouverez ce qu’est la matrice jacobienne et comment la calculer à l’aide d’un exemple. De plus, vous avez plusieurs exercices résolus sur les matrices jacobiennes afin que vous puissiez vous entraîner. Vous verrez également pourquoi le déterminant de la matrice jacobienne, le jacobien, est si important. Enfin, nous expliquons les relations que cette matrice entretient avec d’autres opérations et les applications dont elle dispose.

Qu’est-ce que la matrice jacobienne ?

La définition de la matrice jacobienne est la suivante :

La matrice jacobienne est une matrice formée par les dérivées partielles du premier ordre d’une fonction.

La formule de la matrice jacobienne est donc la suivante :

Par conséquent, les matrices jacobiennes auront toujours autant de lignes que les fonctions scalaires

$(f_1,f_2,\ldots ,f_m)$ avoir la fonction, et le nombre de colonnes correspondra au nombre de variables $(x_1, x_2, \ldots , x_n).$

D’autre part, cette matrice est également connue sous le nom de carte différentielle jacobienne ou carte linéaire jacobienne . En fait, parfois, il est également écrit avec la lettre D au lieu de la lettre J :

$\displaystyle J_f = D_f$

Par curiosité, la matrice jacobienne porte le nom de Carl Gustav Jacobi, un important mathématicien et professeur du XIXe siècle qui a apporté d’importantes contributions au monde des mathématiques, en particulier dans le domaine de l’algèbre linéaire.

Exemple de calcul de la matrice jacobienne

Une fois que nous aurons vu le concept de la matrice jacobienne, nous verrons étape par étape comment elle est calculée à l’aide d’un exemple :

Déterminez la matrice jacobienne au point (1,2) de la fonction suivante :

$\displaystyle f(x,y)= (x^4 +3y^2x \ , \ 5y^2-2xy+1)$

La première chose que nous devons faire est de calculer toutes les dérivées partielles du premier ordre de la fonction :

$\displaystyle \cfrac{\partial f_1}{\partial x} = 4x^3+3y^2$

$\displaystyle \cfrac{\partial f_1}{\partial y} = 6yx$

$\displaystyle \cfrac{\partial f_2}{\partial x} = -2y$

$\displaystyle \cfrac{\partial f_2}{\partial y} = 10y-2x$

Maintenant, nous appliquons la formule de la matrice jacobienne. Dans ce cas, la fonction a deux variables et deux fonctions scalaires, donc la matrice jacobienne sera une matrice carrée de dimension 2×2 :

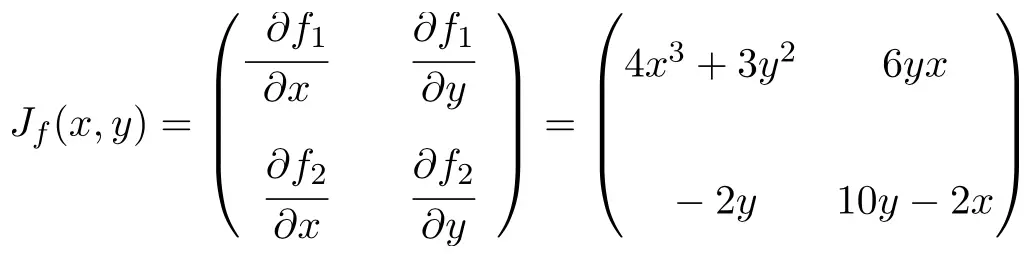
Une fois que nous avons l’expression de la matrice jacobienne, nous l’évaluons au point (1,2) :

$\displaystyle J_f(1,2)=\begin{pmatrix} 4\cdot 1^3+3\cdot 2^2 & 6\cdot 2 \cdot 1 \\[3ex] -2\cdot 2 & 10\cdot 2-2 \cdot 1 \end{pmatrix}$

Et, enfin, on effectue les opérations et on obtient la solution :

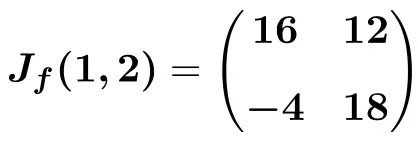
exemple de calcul de la matrice jacobienne

Une fois que vous avez vu comment trouver la matrice jacobienne d’une fonction, nous vous laissons plusieurs exercices résolus étape par étape afin que vous puissiez vous entraîner.

Problèmes résolus des matrices jacobiennes

Exercice 1

Trouvez la matrice jacobienne au point (0,-2) de la fonction vectorielle suivante à 2 variables :

$\displaystyle f(x,y)= (e^{xy}+y \ , \ y^2x)$

voir solution

La fonction a deux variables et deux fonctions scalaires, donc la matrice jacobienne sera une matrice carrée de taille 2×2 :

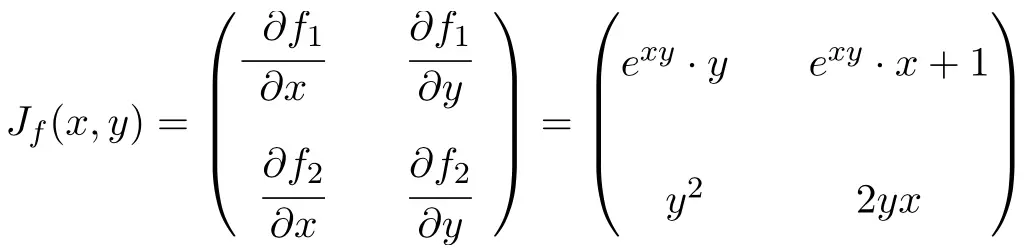
Une fois que nous avons calculé l’expression de la matrice jacobienne, nous l’évaluons au point (0,-2) :

$\displaystyle J_f(0,-2)=\begin{pmatrix}e^{0\cdot (-2)}\cdot (-2)\phantom{5} & \phantom{5}e^{0\cdot (-2)} \cdot 0 +1 \\[4ex](-2)^2 & 2\cdot (-2) \cdot 0 \end{pmatrix}$

Et, enfin, on effectue les opérations et on obtient le résultat :

$\displaystyle \bm{J_f(0,-2)}=\begin{pmatrix} \bm{-2} & \bm{1} \\[1.5ex] \bm{4} & \bm{0} \end{pmatrix}$

Exercice 2

Calculer la matrice jacobienne au point (2,-1) de la fonction suivante à 2 variables :

$\displaystyle f(x,y)= (x^3y^2 - 5x^2y^2 \ , \ y^6-3y^3x+7)$

voir solution

Dans ce cas, la fonction a deux variables et deux fonctions scalaires, donc la matrice jacobienne sera une matrice carrée d’ordre 2 :

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}3x^2y^2-10xy^2& 2x^3y-10x^2y \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -3y^3 & 6y^5-9y^2x \end{pmatrix}$

Une fois que nous avons trouvé l’expression de la matrice jacobienne, nous l’évaluons au point (2,-1) :

$\displaystyle J_f(2,-1)=\begin{pmatrix} 3\cdot 2^2\cdot (-1)^2-10\cdot 2 \cdot (-1)^2\phantom{5} & \phantom{5}2\cdot 2^3\cdot (-1)-10\cdot 2^2\cdot (-1) \\[4ex] -3(-1)^3 & 6\cdot (-1)^5-9\cdot (-1)^2\cdot 2 \end{pmatrix}$

Et, enfin, on effectue les opérations et on obtient le résultat :

$\displaystyle \bm{J_f(1,2)}=\begin{pmatrix} \bm{-8} & \bm{24} \\[1.5ex] \bm{3} & \bm{-24} \end{pmatrix}$

Exercice 3

Déterminer la matrice jacobienne au point (2,-2,2) de la fonction suivante à 3 variables :

$\displaystyle f(x,y,z)= \left(z\tan (x^2-y^2) \ , \ xy\ln \left( \frac{z}{2} \right)\right)$

voir solution

Dans ce cas, la fonction a trois variables et deux fonctions scalaires, par conséquent, la matrice jacobienne sera une matrice rectangulaire de dimension 2×3 :

$\displaystyle J_f(x,y,z)= \begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} &\cfrac{\partial f_2}{\partial z}\end{pmatrix}$

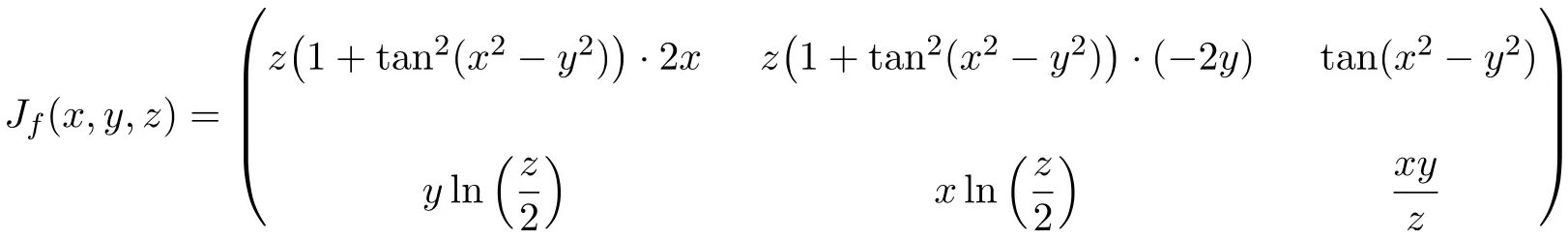
Matrice jacobienne résolu exercice de 3 variables

Une fois que nous avons l’expression de la matrice jacobienne, nous l’évaluons au point (2,-2,2) :

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot 2\cdot 2 & 2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot (-2\cdot (-2)) & \tan (2^2-(-2)^2)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} \displaystyle -2\ln \left( \frac{2}{2} \right) & \displaystyle 2\ln \left( \frac{2}{2} \right) &\displaystyle \frac{2\cdot (-2)}{2} \right)\end{pmatrix}$

Nous effectuons les calculs :

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (0)\bigr) \cdot 4 \phantom{5} & 2\bigl(1+\tan^2 (0)\bigr) \cdot 4 & \phantom{5}\tan (0)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -2\cdot 0 & 2\cdot 0 &-2 \right)\end{pmatrix}$

Et nous continuons à fonctionner jusqu’à ce qu’il ne puisse plus être simplifié :

$\displaystyle \bm{J_f(2,-2,2)=} \begin{pmatrix}\bm{8} & \bm{8} & \bm{0} \\[2ex] \bm{0} & \bm{0} &\bm{-2} \right)\end{pmatrix}$

Exercice 4

Déterminer la matrice jacobienne au point

$(\pi, \pi)$ de la fonction multivariable suivante :

$\displaystyle f(x,y)= \left( \frac{\cos (x-y)}{x} \ , \ e^{x^2-y^2} \ , \ x^3\sin (2y) \right)$

voir solution

Dans ce cas, la fonction a deux variables et trois fonctions scalaires, par conséquent, la matrice jacobienne sera une matrice rectangulaire de dimension 3×2 :

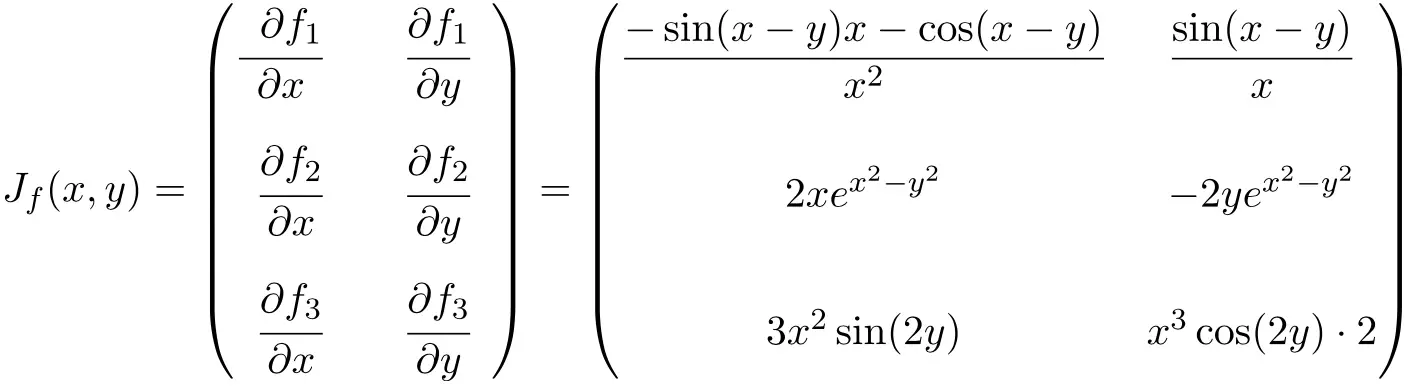
exercice résolu pas à pas de la matrice jacobienne

Une fois que nous avons l’expression de la matrice jacobienne, nous l’évaluons au point

$(\pi, \pi):$

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\frac{-\sin(\pi-\pi)\pi-\cos(\pi-\pi)}{\pi^2} & \displaystyle\frac{\sin (\pi- \pi)}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{\pi^2-\pi^2} & -2\pi e^{\pi^2-\pi^2} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\sin(2\pi) & \pi^3 \cos(2\pi)\cdot 2 \end{pmatrix}$

Nous réalisons les opérations :

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\displaystyle\frac{-0-1}{\pi^2} & \displaystyle\frac{0}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{0} & -2\pi e^{0} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\cdot 0 & \pi^3 \cdot 1 \cdot 2 \end{pmatrix}$

Ainsi la matrice jacobienne de la fonction vectorielle au point considéré vaut :

$\displaystyle \bm{J_f(\pi,\pi)=} \begin{pmatrix}\displaystyle -\frac{\bm{1}}{\bm{\pi^2}} & \bm{0} \\[3ex] \bm{2\pi} & \bm{-2\pi}\\[3ex]\bm{0} & \bm{2\pi^3} \right)\end{pmatrix}$

Exercice 5

Calculer la matrice jacobienne au point

$(3,0,\pi)$ de la fonction suivante à 3 variables :

$\displaystyle f(x,y,z)= \left(xe^{2y}\cos(-z) \ , \ (y-2)^3\cdot \sin\left(\frac{z}{2}\right) \ , \ e^{2y}\cdot \ln\left(\frac{x}{3}\right) \right)$

voir solution

Dans ce cas, la fonction est de trois variables et trois fonctions scalaires, donc, la matrice jacobienne sera une matrice carrée de dimension 3×3 :

$\displaystyle J_f(x,y,z)=\begin{pmatrix}\phantom{5}\cfrac{\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} & \cfrac{\partial f_2}{\partial z} \\[3ex] \cfrac{\partial f_3}{\partial x} & \cfrac{\partial f_3}{\partial y} & \cfrac{\partial f_3}{\partial z}\end{pmatrix}$

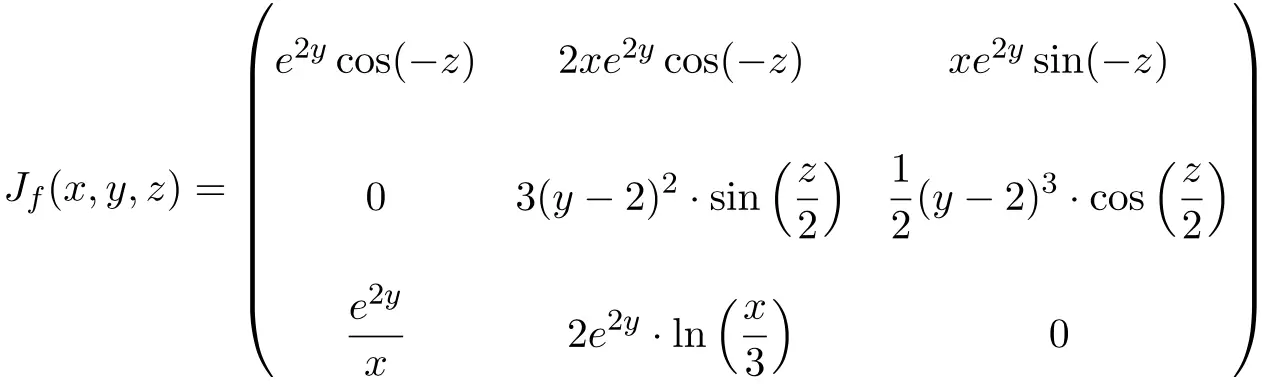
Exercice résolu de matrice jacobienne 3x3 à 3 variables

Une fois que nous avons trouvé la matrice jacobienne, nous l’évaluons au point

$(3,0,\pi):$

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} e^{2\cdot 0}\cos(-\pi) & 2\cdot 3e^{2\cdot 0}\cos(-\pi) & 3e^{2\cdot 0}\sin(-\pi) \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3(0-2)^2\cdot \sin\left(\frac{\pi}{2}\right) & \displaystyle\frac{1}{2}(0-2)^3\cdot \cos\left(\frac{\pi}{2}\right)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{e^{2\cdot 0}}{3} &\displaystyle 2e^{2\cdot 0}\cdot \ln\left(\frac{3}{3}\right) & 0\end{pmatrix}$

On calcule les opérations :

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} 1\cdot (-1) & 6\cdot 1\cdot (-1) & 3\cdot 1 \cdot 0 \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3\cdot 4 \cdot 1 & \displaystyle\frac{1}{2}\cdot (-8)\cdot 0\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{1}{3} &\displaystyle 2\cdot 1\cdot 0 & 0\end{pmatrix}$

Et le résultat de la matrice jacobienne au point est :

$\displaystyle \bm{J_f(3,0,\pi)=} \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} \bm{-1} & \bm{-6} & \phantom{-}\bm{0} \\[2ex] \bm{0} & \bm{12} & \displaystyle \bm{0} \\[2ex] \displaystyle \frac{\bm{1}}{\bm{3}} &\bm{0}& \bm{0}\end{pmatrix}$

Déterminant de la matrice jacobienne : le jacobien

Le déterminant de la matrice jacobienne est appelé déterminant jacobien ou jacobien. Il faut tenir compte du fait que le jacobien ne peut être calculé que si la fonction a le même nombre de variables que les fonctions scalaires, car alors la matrice jacobienne aura le même nombre de lignes que de colonnes et, par conséquent, ce sera une matrice carrée . .

Exemple jacobien

Voyons un exemple de calcul du déterminant jacobien d’une fonction à deux variables :

$\displaystyle f(x,y)= (x^2-y^2 \ , \ 2xy)$

On calcule d’abord la matrice jacobienne de la fonction :

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2x \phantom{5}& -2y \\[2ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 2y & 2x \end{pmatrix}$

Et maintenant on résout le déterminant de la matrice 2×2 :

$\displaystyle \text{det}\bigl(J_f(x,y)\bigr) =\begin{vmatrix} 2x&-2y \\[2ex] 2y & 2x \end{vmatrix} = \bm{4x^2+4y^2}$

Le jacobien et l’inversibilité d’une fonction

Maintenant que vous avez vu le concept du Jacobien, vous avez sûrement pensé… et à quoi ça sert ?

Eh bien, la principale utilité du jacobien est de déterminer si une fonction peut être inversée. Le théorème de la fonction inverse dit que si le déterminant de la matrice jacobienne (le jacobien) est différent de 0, cela signifie que cette fonction est inversible.

$\displaystyle \text{det}\bigl(J_f\bigr) \neq 0 \ \longrightarrow \ \exists \ f^{-1}$

Il convient de noter que cette condition est nécessaire mais pas suffisante, c’est-à-dire que si le déterminant est différent de zéro, nous pouvons affirmer que la matrice peut être inversée, cependant, si le déterminant est égal à 0, nous ne pouvons pas savoir si la fonction a une inverse ou Non.

Par exemple, dans l’exemple vu précédemment de comment trouver le jacobien d’une fonction, le déterminant donne

$4x^2+4y^2$ . Dans ce cas, nous pouvons affirmer que la fonction peut toujours être inversée sauf au point (0,0), car ce point est le seul où le déterminant jacobien est égal à zéro et, par conséquent, nous ne savons pas si l’inverse fonction existe dans ce point.

Relation de la matrice jacobienne avec d’autres opérations

La matrice jacobienne est liée au gradient et à la matrice hessienne d’une fonction :

Pente

Si la fonction est une fonction scalaire, la matrice jacobienne sera une matrice ligne qui sera équivalente au gradient :

$\displaystyle f: \mathbb{R}^n \to \mathbb{R}$

$\displaystyle J_f = \nabla f = \begin{pmatrix}\phantom{5} \cfrac{\partial f}{\partial x_1} \phantom{5}& \cfrac{\partial f}{\partial x_2}& \dots & \cfrac{\partial f}{\partial x_n}\phantom{5} \end{pmatrix}$

Matrice de Hesse

La matrice jacobienne du gradient d’une fonction est égale à la matrice hessienne :

$\displaystyle H_f = J(\nabla f)$

La Hessienne est une matrice très importante pour la dérivation de fonctions à plus d’une variable, car elle est formée par les dérivées secondes de la fonction. En fait, on pourrait dire que la matrice hessienne est la continuité de la matrice jacobienne. Mais c’est tellement important que nous avons une page entière qui l’explique en détail. Donc, si vous souhaitez savoir exactement ce qu’est cette matrice et pourquoi elle est si spéciale, vous pouvez cliquer sur le lien.

Applications de la matrice jacobienne

Outre l’utilité que nous avons vue du jacobien, qui détermine si une fonction est inversible, la matrice jacobienne a d’autres applications.

La matrice jacobienne est utilisée pour calculer les points critiques d’une fonction multivariée, qui sont ensuite classés en maximums, minimums ou points de selle à travers la matrice hessienne. Pour trouver les points critiques, vous devez calculer la matrice jacobienne de la fonction, la mettre égale à 0 et résoudre les équations résultantes.

$\displaystyle J_f(x)=0$

De plus, une autre application de la matrice jacobienne se trouve dans l’intégration de fonctions à plus d’une variable, c’est-à-dire dans les intégrales doubles, triples, etc. Puisque le déterminant de la matrice jacobienne permet un changement de variable en intégrales multiples selon la formule suivante :

$\displaystyle x=T(x^*)$

$\displaystyle \int_\Omega f(x)dx=\int_{\Omega^*} f\bigl(T(x^*)\bigr)\cdot \begin{vmatrix} \text{det}\bigl(JT(x^*)\bigr)\end{vmatrix} dx^*$

Où T est la fonction de changement de variable qui relie les variables d’origine aux nouvelles.

Enfin, la matrice jacobienne est également utilisée pour faire une approximation linéaire de toute fonction

$f$ autour d’un point $p$ :

$\displaystyle f(x) \approx f(p) + J_f(p)(x-p)$

Qu’est-ce que la matrice jacobienne ?

Exemple de calcul de la matrice jacobienne

Problèmes résolus des matrices jacobiennes

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Déterminant de la matrice jacobienne : le jacobien

Exemple jacobien

Le jacobien et l’inversibilité d’une fonction

Relation de la matrice jacobienne avec d’autres opérations

Pente

Matrice de Hesse

Applications de la matrice jacobienne

Leave a Comment Cancel Reply