Matrice de Hesse (ou Hesse) -

Cette page est sûrement l’explication la plus complète de la matrice Hessienne qui existe. Ici, le concept de la matrice de Hesse est expliqué, comment le calculer avec des exemples et il y a même plusieurs exercices résolus à pratiquer. De plus, vous pourrez apprendre comment les valeurs maximales et minimales d’une fonction à plusieurs variables sont calculées, ainsi que savoir s’il s’agit d’une fonction concave ou convexe. Et enfin, vous trouverez également les utilitaires et applications de la matrice hessienne.

Qu’est-ce que la matrice de Hesse ?

La définition de la matrice hessoise (ou hessienne) est la suivante :

La matrice hessienne est une matrice carrée de dimension n × n composée des dérivées secondes partielles d’une fonction de n variables.

Cette matrice est également connue sous le nom de Hessian, ou même dans certains livres de mathématiques, elle est nommée Discriminant. Mais la façon la plus courante de l’appeler est la matrice de Hesse.

La formule de la matrice hessienne est donc la suivante :

Par conséquent, la matrice hessienne sera toujours une matrice carrée dont la dimension sera égale au nombre de variables de la fonction. Par exemple, si la fonction a 3 variables, la matrice Hessienne aura la dimension 3×3.

De plus, le théorème de Schwarz (ou théorème de Clairaut) dit que l’ordre de différenciation n’a pas d’importance, c’est-à-dire dériver partiellement d’abord par rapport à la variable

$x_1$ puis par rapport à la variable $x_2$ revient à différencier partiellement par rapport à $x_2$ puis respecter $x_1$ .

$\displaystyle \cfrac{\partial^2 f}{\partial x_i\partial x_j} = \cfrac{\partial^2 f}{\partial x_j\partial x_i}$

Par conséquent, la matrice hessienne est une matrice symétrique , ou en d’autres termes, elle a une symétrie dont l’axe est sa diagonale principale.

Par curiosité, la matrice de Hesse porte le nom de Ludwig Otto Hesse, un mathématicien allemand du XIXe siècle qui a apporté des contributions très importantes au domaine de l’algèbre linéaire.

Exemple de calcul de la matrice Hessienne

Voyons un exemple de comment trouver une matrice hessienne de dimension 2 × 2 :

Calculez la matrice hessienne au point (1,0) de la fonction suivante :

$\displaystyle f(x,y)=y^4+x^3+3x^2+ 4y^2 -4xy -5y +8$

Tout d’abord, nous devons calculer les dérivées partielles du premier ordre :

$\displaystyle \cfrac{\partial f}{\partial x} = 3x^2 +6x -4y$

$\displaystyle \cfrac{\partial f}{\partial y} = 4y^3+8y -4x -5$

Une fois que nous connaissons déjà les dérivées premières, nous calculons toutes les dérivées partielles du second ordre :

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 6x +6$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =12y^2 +8$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}= -4$

Par conséquent, nous pouvons maintenant trouver la matrice hessienne à partir de la formule des matrices 2 × 2 :

$\displaystyle H_f (x,y)=\begin{pmatrix}\cfrac{\partial^2 f}{\partial x^2} & \cfrac{\partial^2 f}{\partial x \partial y} \\[4ex] \cfrac{\partial^2 f}{\partial y \partial x} & \cfrac{\partial^2 f}{\partial y^2} \end{pmatrix}$

$\displaystyle H_f (x,y)=\begin{pmatrix}6x +6 &-4 \\[2ex] -4 & 12y^2+8 \end{pmatrix}$

Ainsi la matrice Hessienne évaluée au point (1,0) sera :

$\displaystyle H_f (1,0)=\begin{pmatrix}6(1) +6 &-4 \\[2ex] -4 & 12(0)^2+8 \end{pmatrix}$

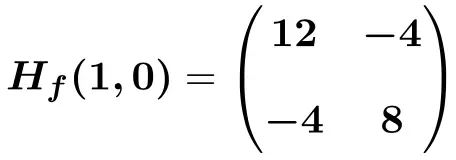
exemples de matrice de toile de jute ou de toile de jute

Problèmes résolus des matrices de Hesse

Exercice 1

Calculer la matrice hessienne de la fonction suivante à 2 variables au point (1,1) :

$\displaystyle f(x,y)=x^2y+y^2x$

voir solution

Tout d’abord, il faut trouver les dérivées partielles du premier ordre de la fonction :

$\displaystyle \cfrac{\partial f}{\partial x} = 2xy+y^2$

$\displaystyle \cfrac{\partial f}{\partial y} = x^2+2yx$

Une fois que nous avons déjà calculé les dérivées premières, nous procédons à la résolution de toutes les dérivées partielles du second ordre :

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 2y$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =2x$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}=2x+2y$

Ainsi la matrice Hessienne est définie comme suit :

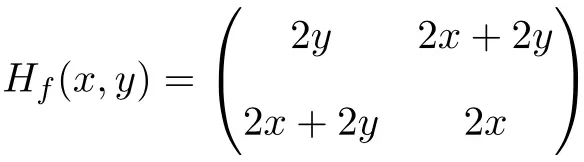
Exercice résolu de la Hessienne ou matrice Hessienne de dimension 2x2

Enfin, il ne reste plus qu’à évaluer la matrice hessienne au point (1,1) :

$\displaystyle H_f (1,1)=\begin{pmatrix}2\cdot 1 &2 \cdot 1+2\cdot 1 \\[1.5ex] 2\cdot 1+2\cdot 1 & 2\cdot 1 \end{pmatrix}$

$\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{2} & \bm{4} \\[1.1ex] \bm{4} & \bm{2} \end{pmatrix}$

Exercice 2

Calculez le hessien au point (1,1) de la fonction suivante à deux variables :

$\displaystyle f(x,y)= e^{y\ln x}$

voir solution

Tout d’abord, nous devons calculer les dérivées partielles du premier ordre de la fonction :

$\displaystyle \cfrac{\partial f}{\partial x} = e^{y\ln x} \cdot \cfrac{y}{x}$

$\displaystyle \cfrac{\partial f}{\partial y} = e^{y\ln x} \cdot \ln x$

Une fois que nous avons les dérivées premières, nous calculons les dérivées partielles du second ordre de la fonction :

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = e^{y\ln x} \cdot \cfrac{y^2}{x^2} - e^{y\ln x} \cdot \cfrac{y}{x^2}$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =e^{y\ln x} \cdot \ln ^2 x$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =e^{y\ln x} \cdot \cfrac{y}{x}\cdot \ln x + e^{y\ln x}\cdot \cfrac{1}{x}$

Ainsi la matrice hessienne de la fonction est une matrice carrée de dimension 2×2 :

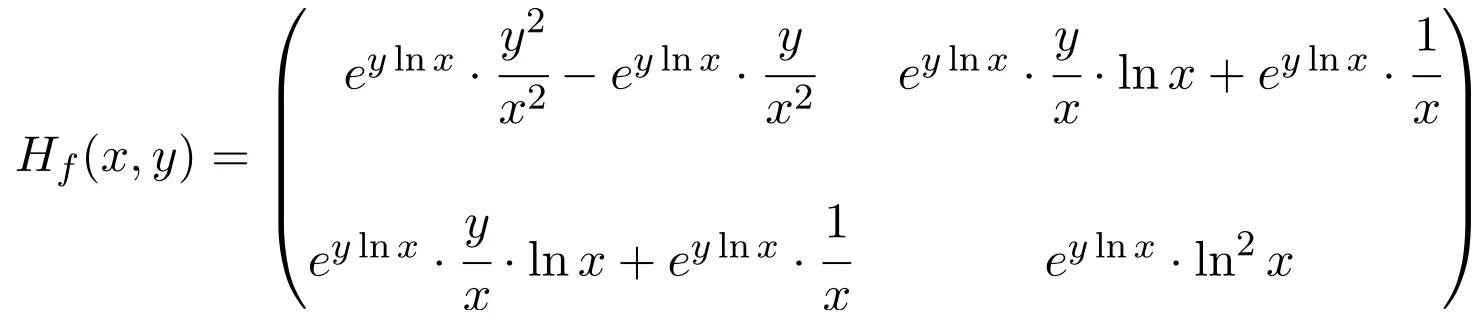
Exercice résolu de Hesse ou matrice de Hesse de dimension 2x2

Enfin, il ne reste plus qu’à évaluer la matrice hessienne au point (1,1) :

$\displaystyle H_f (1,1)=\begin{pmatrix} e^{1\ln (1)} \displaystyle \cdot \cfrac{1^2}{1^2} - e^{1\ln (1)} \cdot \cfrac{1}{1^2}& e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} \\[3ex] e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} & e^{1\ln (1)} \cdot \ln ^2 (1) \end{pmatrix}$

$\displaystyle H_f (1,1)=\begin{pmatrix}e^{0} \cdot 1 - e^{0} \cdot 1& e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 \\[2ex] e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 & e^{0} \cdot 0\end{pmatrix}$

$\displaystyle H_f (1,1)=\begin{pmatrix}1 - 1& 0+ 1 \\[1.5ex] 0 +1 & 1 \cdot 0\end{pmatrix}$

$\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{0} & \bm{1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}$

Exercice 3

Trouver la matrice hessienne au point

$(0,1,\pi)$ de la fonction suivante à 3 variables :

$\displaystyle f(x,y,z)= e^{-x}\cdot \text{sen}(yz)$

voir solution

Tout d’abord, nous calculons les dérivées partielles du premier ordre de la fonction :

$\displaystyle \cfrac{\partial f}{\partial x} = -e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial f}{\partial y} = ze^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial f}{\partial z} = ye^{-x}\cdot \text{cos}(yz)$

Une fois que nous avons les dérivées premières, nous calculons les dérivées partielles du second ordre de la fonction :

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} =e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =-ze^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x} =-ye^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =-z^2e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial z \partial y} =e^{-x}\cdot \text{cos}(yz)-yze^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 z} = -y^2e^{-x}\cdot \text{sen}(yz)$

Si bien que la matrice hessienne de la fonction est une matrice carrée de dimension 3×3 :

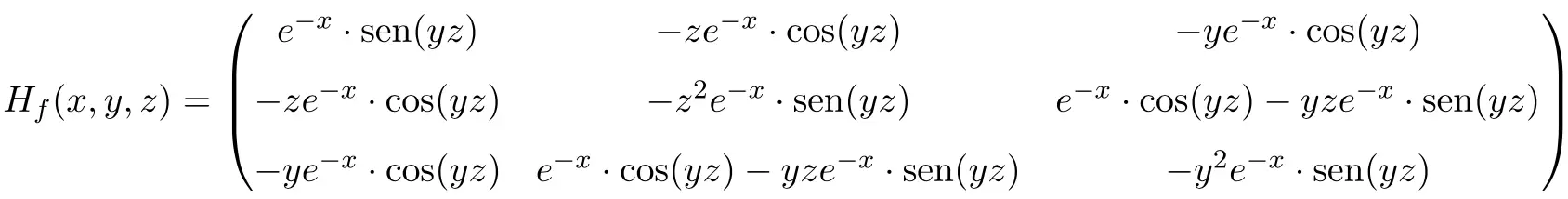
exemple de toile de jute ou matrice de toile de jute de dimension 3x3

Enfin, nous remplaçons les variables par leurs valeurs respectives au point

$(0,1,\pi):$

$\displaystyle H_f(0,1,\pi)=\begin{pmatrix}e^{-0}\cdot \text{sen}(1\pi) & -\pi e^{-0}\cdot \text{cos}(1\pi) &-1e^{-0}\cdot \text{cos}(1\pi) \\[1.5ex] -\pi e^{-0}\cdot \text{cos}(1 \pi)&-\pi^2e^{-0}\cdot \text{sen}(1 \pi) &e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi) \\[1.5ex] -1e^{-0}\cdot \text{cos}(1 \pi)& e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi)& -1^2e^{-0}\cdot \text{sen}(1 \pi) \end{pmatrix}$

$\displaystyle H_f(0,1,\pi)=\begin{pmatrix}1\cdot 0 & -\pi \cdot 1 \cdot (-1)&-1\cdot 1 \cdot (-1) \\[1.5ex] -\pi \cdot 1 \cdot (-1) &-\pi^2\cdot 1\cdot 0 &1 \cdot (-1)-\pi \cdot 1\cdot 0 \\[1.5ex] -1\cdot 1 \cdot (-1) & 1\cdot (-1) - \pi \cdot 1\cdot 0 & -1\cdot 1 \cdot 0 \end{pmatrix}$

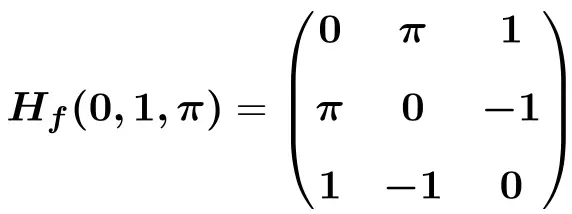
exercice résolu pas à pas de hessienne ou matrice hessienne de dimension 3x3

Exercice 4

Déterminer la matrice hessienne au point (2,-1,1,-1) de la fonction suivante à 4 variables :

$\displaystyle f(x,y,z,w)= 2x^3y^4zw^2 - 2y^3w^4+ 3x^2z^2$

voir solution

La première étape consiste à trouver les dérivées partielles du premier ordre de la fonction :

$\displaystyle \cfrac{\partial f}{\partial x} =6x^2y^4zw^2 + 6xz^2$

$\displaystyle \cfrac{\partial f}{\partial y} =8x^3y^3zw^2 - 6y^2w^4$

$\displaystyle \cfrac{\partial f}{\partial z} = 2x^3y^4w^2 + 6x^2z$

$\displaystyle \cfrac{\partial f}{\partial w} =4x^3y^4zw - 8y^3w^3$

Maintenant, nous résolvons les dérivées partielles du second ordre de la fonction :

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} =12xy^4zw^2 + 6z^2$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x}=24x^2y^3zw^2$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x}=6x^2y^4w^2 + 12xz$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial w} = \cfrac{\partial^2 f}{\partial w \partial x}=12x^2y^4zw$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =24x^3y^2zw^2 - 12yw^4$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial y \partial z}=8x^3y^3w^2$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial w} = \cfrac{\partial^2 f}{\partial w \partial y}=16x^3y^3zw - 24y^2w^3$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 z} =6x^2$

$\displaystyle \cfrac{\partial^2 f}{\partial z \partial w} = \cfrac{\partial^2 f}{\partial w \partial z}=4x^3y^4w$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 w} =4x^3y^4z - 24y^3w^2$

Ainsi l’expression de la matrice hessienne 4×4 obtenue en résolvant toutes les dérivées partielles est la suivante :

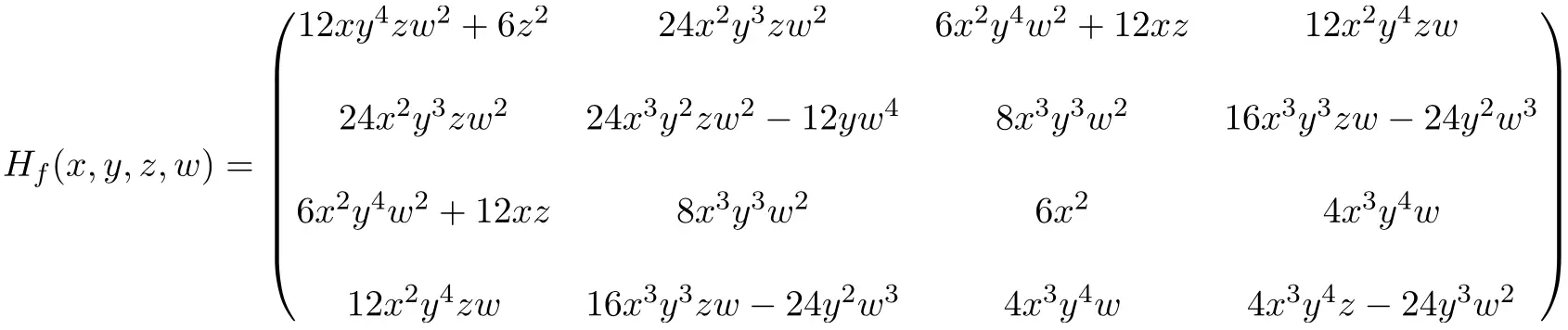
exemple résolu pas à pas de toile de jute ou matrice de toile de jute de dimension 4x4

Enfin, on substitue les inconnues à leurs valeurs ponctuelles respectives (2,-1,1,-1) et on fait les calculs :

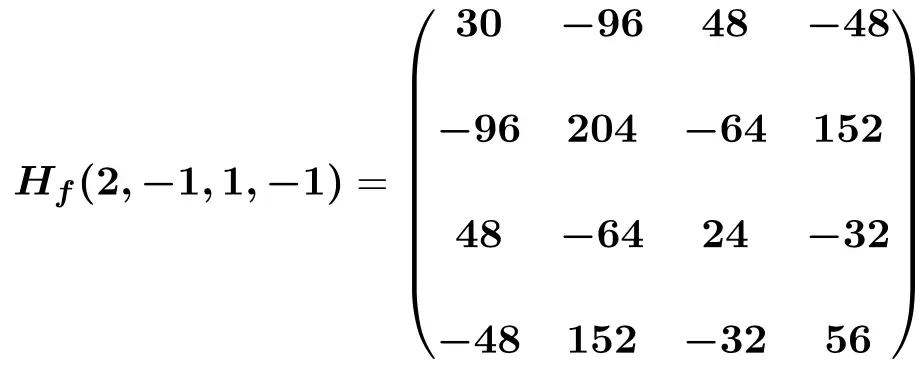
Exercice résolu pas à pas de Hessian ou Hessian matrix de dimension 4x4

Comment savoir quand la matrice hessienne est positive, négative ou indéfinie ?

Comme nous le verrons plus loin, savoir si la matrice hessienne est une matrice semi-définie positive, définie positive, semi-définie négative, définie négative ou indéfinie est très utile. Voyons donc comment nous pouvons le savoir :

Critère de valeurs propres (ou valeurs propres)

Une façon de savoir de quel type de matrice il s’agit est de passer par les valeurs propres (ou valeurs propres) de la matrice hessienne :

La matrice hessienne est semi-définie positive si elle a des valeurs propres (ou valeurs propres) égales et supérieures à zéro. C’est-à-dire qu’il a des valeurs propres positives et au moins une égale à 0 :

$\lambda \geq 0$

La matrice hessienne est définie positive si toutes ses valeurs propres (ou valeurs propres) sont exclusivement supérieures à 0 (positives) :

$\lambda > 0$

La matrice de Hesse est semi-définie négative si elle a des valeurs propres (ou des valeurs propres) égales et inférieures à zéro. C’est-à-dire qu’il a des valeurs propres négatives et au moins une égale à 0 :

$\lambda \leq 0$

La matrice hessienne est définie négative si toutes ses valeurs propres (ou valeurs propres) ne sont inférieures à 0 (négatives) :

$\lambda < 0$

La matrice hessienne est indéfinie lorsqu’elle a des valeurs propres (ou valeurs propres) positives et négatives :

$\lambda > 0 \qquad \lambda <0$

Critère de Sylvester

Une autre façon de savoir de quel type est la matrice hessienne est d’utiliser le critère de Sylvester, bien que ce théorème nous permette seulement de savoir si elle est définie positive, définie négative ou indéfinie. Mais parfois, il peut être beaucoup plus rapide à utiliser car les calculs sont généralement plus faciles.

Ainsi, le critère de Sylvester se lit comme suit :

Si tous les principaux mineurs de la matrice hessienne sont supérieurs à 0, c’est une matrice définie positive .

Si les principaux mineurs de la matrice hessienne à index pair sont supérieurs à 0 et ceux à index impair sont inférieurs à 0, il s’agit d’une matrice définie négative .

Si tous les principaux mineurs de la matrice hessienne sont différents de 0 et qu’aucune des deux conditions précédentes n’est remplie, c’est une matrice indéfinie .

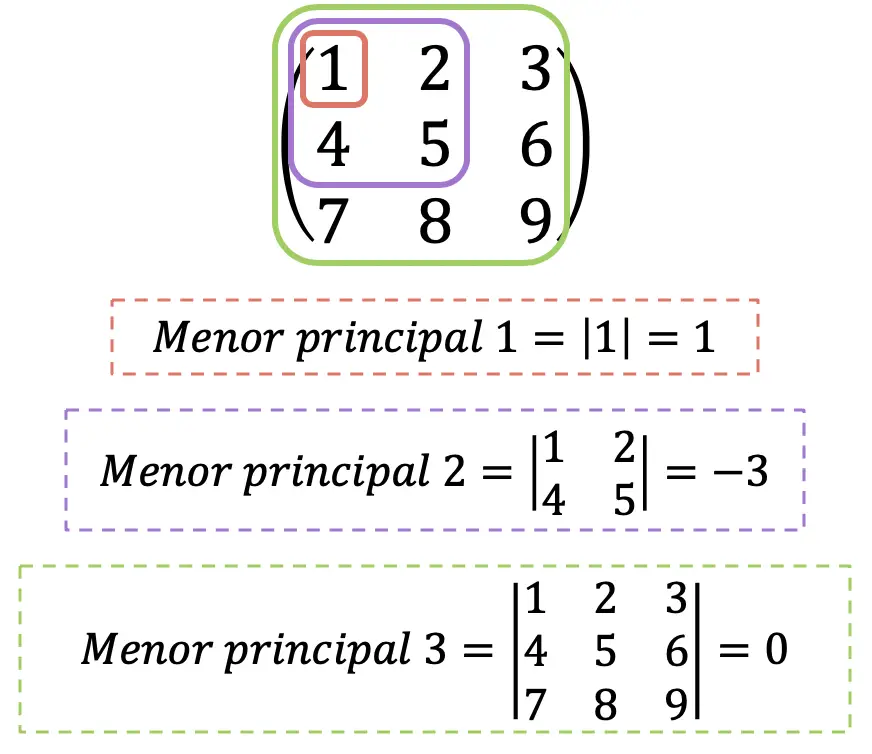
mineurs principaux d'une matrice hessoise

Évidemment, le mineur principal maximum de la matrice hessienne coïncidera toujours avec son déterminant. A titre informatif uniquement, le déterminant de la matrice Hessienne est également appelé “le Hessien”, bien que nous ne le ferons pas ici pour éviter toute confusion.

Comment calculer un maximum ou un minimum d’une fonction avec la matrice Hessienne

Une fois que vous savez comment calculer la matrice Hessienne, vous vous demandez sûrement : et à quoi sert cette matrice ?

Eh bien, l’une des applications de la matrice hessienne est de trouver le maximum ou le minimum d’une fonction avec plus d’une variable. Voici une explication étape par étape de la méthode de calcul des maximums et des minimums :

Tout d’abord, les points critiques de la fonction multivariable sont calculés. Pour ce faire, on calcule le gradient ou la matrice jacobienne de la fonction, on le met égal à 0 et on résout les équations.
La matrice de Hesse est calculée.
Les points critiques trouvés à l’étape 1 sont substitués dans la matrice hessienne. On obtiendra ainsi autant de matrices hessiennes que de points critiques ont la fonction.
Nous regardons quel type de matrice est chaque matrice hessienne. Autrement dit, nous regardons pour voir s’il est défini positif, défini négatif, indéfini, etc.
- Si la matrice hessienne est définie positive, le point critique est un minimum relatif de la fonction.
- Si la matrice hessienne est définie négative, le point critique est un maximum relatif de la fonction.
- Si la matrice hessienne est indéfinie, le point critique est un point selle .

Exemple de calcul des maximums et des minimums d’une fonction multivariable

Pour voir comment cela se fait, voici un exemple de calcul et de classification des extrema relatifs d’une fonction à l’aide de la matrice hessienne :

Trouvez tous les extrema relatifs de la fonction multivariable suivante :

$\displaystyle f(x,y)=x^2-y^2+2xy+ 4x-4y$

La première chose que nous devons faire est de calculer la matrice jacobienne de la fonction, qui dans ce cas coïncidera avec le gradient car il s’agit d’une fonction scalaire :

$\displaystyle \nabla f (x,y)=(2x+2y+4 \ , \ -2y+2x-4 )$

Il faut maintenant déterminer les points critiques, pour cela on égalise les équations obtenues à 0 et on résout le système d’équations :

$\displaystyle \nabla f (x,y)=0$

$\displaystyle \left. \begin{array}{l} 2x+2y+4 =0 \\[2ex] -2y+2x-4=0 \end{array}\right\} \longrightarrow \left. \begin{array}{c} x = 0 \\[1.1ex] y = -2 \end{array}\right\} \longrightarrow \ (0,-2)$

Donc le point critique que nous avons trouvé est (0,-2).

Une fois le point critique de la fonction trouvé, il faut calculer la matrice hessienne :

$\displaystyle H_f (x,y)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}$

Et, évidemment, la matrice hessienne évaluée au point critique est la même :

$\displaystyle H_f (0,-2)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}$

Pour voir de quel type de matrice il s’agit, nous utiliserons le critère de Sylvester. On résout donc les principaux mineurs de la matrice :

$\displaystyle \begin{vmatrix}2 \end{vmatrix} = 2$

$\displaystyle \begin{vmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -8$

Le principal mineur 1 (impair) est positif et le principal mineur 2 (pair) est négatif, donc selon le critère de Sylvester, il s’agit d’une matrice indéfinie. Et, par conséquent, le point critique (0,-2) est un point selle.

Déterminer la concavité ou la convexité d’une fonction avec la matrice hessienne

Une autre utilité de la matrice Hessienne est de savoir si une fonction est concave ou convexe. Et cela peut être déterminé selon le théorème suivant :

Être

$A \subseteq \mathbb{R}^n$ un ensemble ouvert et $f \colon A \to \mathbb{R}$ une fonction dont les dérivées secondes sont continues, sa concavité et sa convexité sont définies par la matrice hessienne :

La fonction $f$ est convexe sur l’ensemble $A$ si et seulement si sa matrice hessienne est semi-définie positive en tout point de l’ensemble.
La fonction $f$ est strictement convexe sur l’ensemble $A$ si et seulement si sa matrice hessienne est définie positive en tout point de l’ensemble.

✓ Par conséquent, si

$f$ est une fonction convexe en un point où la matrice jacobienne s’annule également, ce point est un minimum local .

La fonction $f$ est concave dans l’ensemble $A$ si et seulement si sa matrice hessienne est semi-définie négative en tout point de l’ensemble.
La fonction $f$ est strictement concave dans l’ensemble $A$ si et seulement si sa matrice hessienne est définie négative en tout point de l’ensemble.

✓ Par conséquent, si

$f$ est une fonction concave en un point où la matrice jacobienne s’annule également, ce point est un maximum local .

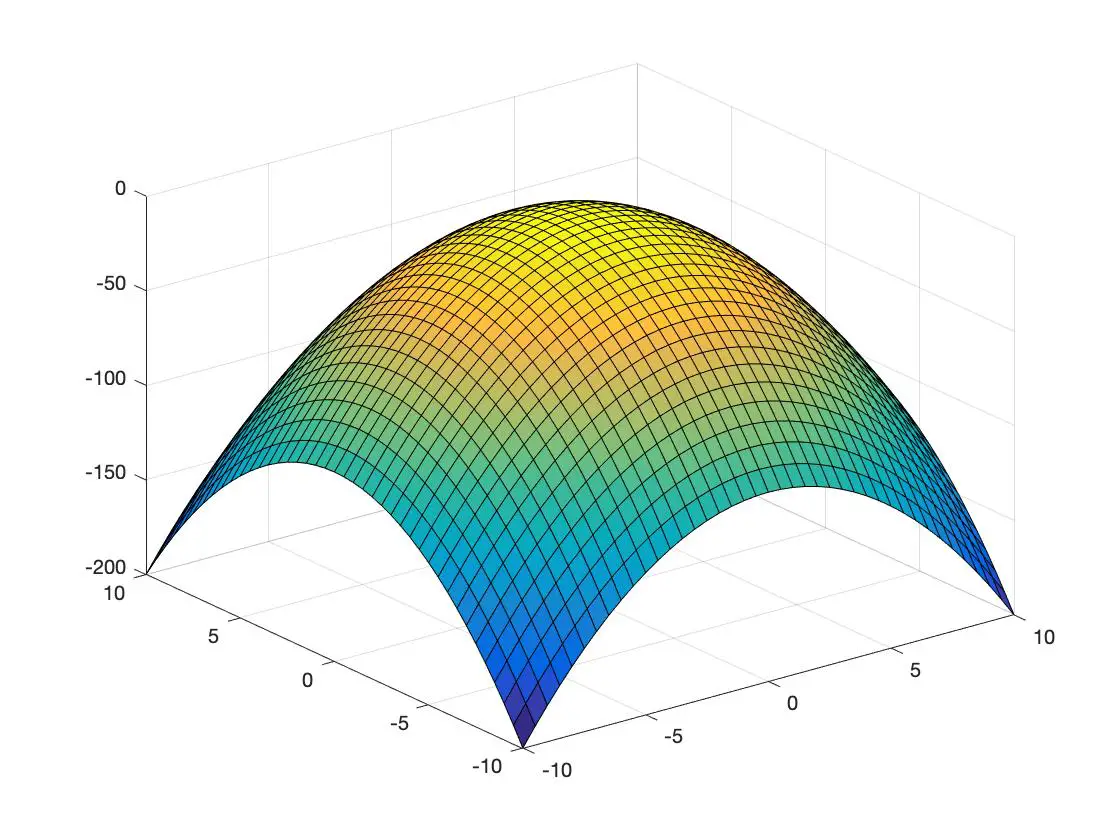
Ci-dessous vous avez un exemple de fonction convexe et un autre de fonction concave représentée dans un espace à 3 dimensions :

fonction convexe

fonction concave

L'image a un attribut ALT vide ; son nom de fichier est concavity-and-convexity-of-a-function-with-the-hessian-matrix-1024x768.jpg

Plus d’applications de la matrice de Hesse

Les principales utilités de la matrice hessienne sont celles que nous avons déjà vues, cependant, elle a aussi d’autres applications. Nous les expliquons ci-dessous pour les plus curieux.

Polynôme de Taylor

Le développement du polynôme de Taylor pour les fonctions de 2 variables ou plus au point

$a$ commence comme ça :

$\displaystyle T(x) = f(a) + (x-a)^T \nabla f(a) + \frac{1}{2}(x-a)^T \operatorname{H}_f(a)(x-a) + \ldots$

Comme vous pouvez le voir, les termes du second ordre du développement de Taylor sont donnés par la matrice hessienne évaluée au point de développement du polynôme.

Matrice de toile de jute bordée

Une autre utilisation de la matrice Hessienne est de calculer les minima et les maxima d’une fonction multivariée

$f(x,y)$ restreint à un autre rôle $g(x,y)$ . Pour résoudre ce problème, la matrice de Hesse bordée est utilisée et la procédure suivante est suivie :

Etape 1 : La fonction de Lagrange est calculée, qui est définie par l’expression suivante :

$\displaystyle L(x,y,\lambda) = f(x,y)+ \lambda \cdot g(x,y)$

Étape 2 : Les points critiques de la fonction de Lagrange sont trouvés. Pour ce faire, nous calculons le gradient de la fonction de Lagrange, définissons les équations égales à 0 et résolvons les équations.

$\displaystyle \nabla L = 0$

$\displaystyle \cfrac{\partial L}{\partial x} = 0 \qquad \cfrac{\partial L}{\partial y}=0 \qquad \cfrac{\partial L}{\partial \lambda}=0$

Étape 3 : Pour chaque point que nous avons trouvé, nous calculons la Hessienne bordée, qui est définie par la matrice suivante :

$\displaystyle H(f,g) = \begin{pmatrix}0 & \cfrac{\partial g}{\partial x_1} & \cfrac{\partial g}{\partial x_2} & \cdots & \cfrac{\partial g}{\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_1} & \cfrac{\partial^2 f}{\partial x_1^2} & \cfrac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_1\,\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_2} & \cfrac{\partial^2 f}{\partial x_2\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_2^2} & \cdots & \cfrac{\partial^2 f}{\partial x_2\,\partial x_n} \\[3ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[3ex] \cfrac{\partial g}{\partial x_n} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_n^2}\end{pmatrix}$

Etape 4 : On détermine pour chaque point critique s’il s’agit d’un maximum ou d’un minimum :

Ce sera un maximum local de la fonction $f$ sous contraintes de fonction $g$ si les nm derniers (où n est le nombre de variables et m le nombre de contraintes) principaux mineurs de la matrice hessienne bordée évalués au point critique ont des signes alternés commençant par le signe négatif.

Ce sera un minimum local de la fonction $f$ sous contraintes de fonction $g$ si les nm derniers (où n est le nombre de variables et m le nombre de contraintes) principaux mineurs de la matrice hessienne tranchante évalués au point critique ont tous des signes négatifs.

Il faut garder à l’esprit que les minima ou maxima relatifs d’une fonction contrainte à une autre ne doivent pas nécessairement l’être pour la fonction non restreinte. La matrice de Hesse bordée n’est donc utile que pour ce type de problème.

Relation avec les autres opérations

Enfin, la matrice hessienne est également liée à d’autres opérations ou matrices importantes, principalement avec la matrice jacobienne et avec l’opérateur de Laplace.

Relation avec la matrice jacobienne

La matrice hessienne d’une fonction

$f$ est la matrice jacobienne du gradient de la même fonction :

$\displaystyle H_f = J(\nabla f)$

Opérateur de Laplace

La trace matricielle hessienne est équivalente à l’ opérateur de Laplace :

$\displaystyle tr( H_f) = \Delta f$

Cette égalité peut être facilement prouvée, puisque la définition de l’opérateur de Laplace est la divergence du gradient d’une fonction :

$\displaystyle \Delta f =\nabla \cdot (\nabla f) = (\nabla \cdot \nabla )f = \nabla^2 f$

Son expression est donc :

$\displaystyle \Delta f = \cfrac{\partial ^2 f}{\partial^2 x_1} +\cfrac{\partial ^2 f}{\partial^2 x_2} + \cfrac{\partial ^2 f}{\partial^2 x_3}+ \ldots +\cfrac{\partial ^2 f}{\partial^2 x_n}$

Et cette somme n’est que la trace de la matrice hessienne, donc l’équivalence est prouvée.

Qu’est-ce que la matrice de Hesse ?

Exemple de calcul de la matrice Hessienne

Problèmes résolus des matrices de Hesse

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Comment savoir quand la matrice hessienne est positive, négative ou indéfinie ?

Critère de valeurs propres (ou valeurs propres)

Critère de Sylvester

Comment calculer un maximum ou un minimum d’une fonction avec la matrice Hessienne

Exemple de calcul des maximums et des minimums d’une fonction multivariable

Déterminer la concavité ou la convexité d’une fonction avec la matrice hessienne

Plus d’applications de la matrice de Hesse

Polynôme de Taylor

Matrice de toile de jute bordée

Relation avec les autres opérations

Relation avec la matrice jacobienne

Opérateur de Laplace

Leave a Comment Cancel Reply