Limites trigonométriques

Vous découvrirez ici comment résoudre les limites trigonométriques. Vous pourrez voir plusieurs exemples de limites de fonctions trigonométriques et même vous entraîner avec des exercices résolus étape par étape sur les limites trigonométriques.

Que sont les limites trigonométriques ?

Les limites trigonométriques sont des limites calculées sur des fonctions trigonométriques. Pour résoudre les limites trigonométriques, une procédure préalable doit être appliquée, car elles donnent généralement lieu à des indéterminations.

De plus, les limites infinies des fonctions trigonométriques n’existent pas, car ce sont des fonctions périodiques. Autrement dit, ses graphiques sont continuellement répétés périodiquement sans tendre vers une valeur spécifique.

Formules de limites trigonométriques

Toutes les limites trigonométriques sont calculées à partir des deux formules suivantes :

Si on essaie de calculer la limite par substitution, on obtient l’indétermination zéro entre zéro :

Mais cette formule trigonométrique peut être démontrée en calculant des valeurs de la fonction de plus en plus proches de x=0 (angles en radians).

Les deux limites latérales de la fonction trigonométrique donnent 1, donc la limite au point x=0 est 1 :

Ainsi, la limite trigonométrique du sinus de x divisé par x lorsque x tend vers 0 est égale à 1.

Cette formule peut également être appliquée pour plusieurs angles :

Si on essaie de trouver la limite par substitution directe, on obtient la forme indéterminée zéro entre zéro :

Mais nous pouvons vérifier l’égalité à partir de la formule ci-dessus. Pour ce faire, il faut d’abord multiplier le numérateur et le dénominateur de la fraction par 1 plus le cosinus de x :

Nous avons maintenant une identité notable au numérateur de la fraction, nous pouvons donc la simplifier :

En partant de l’identité trigonométrique fondamentale, on réécrit le numérateur :

On peut donc transformer la fraction en produit de fractions :

En utilisant les propriétés des limites, nous pouvons convertir l’expression ci-dessus en un produit des limites :

Grâce à la formule démontrée ci-dessus, nous pouvons facilement simplifier la limite trigonométrique :

Et enfin, on calcule la limite résultante :

Par conséquent, la formule limite trigonométrique est vérifiée :

Comme pour l’autre formule, elle peut également être utilisée pour plusieurs angles :

Par conséquent, pour résoudre les limites trigonométriques, nous devons utiliser l’arithmétique pour transformer les fonctions et obtenir des expressions similaires à celles-ci. De cette façon, nous pouvons utiliser l’une des deux formules et trouver la valeur de la limite.

D’un autre côté, nous pouvons parfois avoir besoin d’appliquer certaines identités trigonométriques, nous vous laissons donc toutes les formules ci-dessous

Formule qui relie les trois principaux rapports trigonométriques :

Identité trigonométrique fondamentale :

Relations trigonométriques dérivées de la fondamentale :

Angles opposés :

Somme de deux angles :

Différence de deux angles :

Double angle :

Demi-angle :

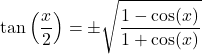
Addition et soustraction de sinus et cosinus :

Produit des sinus et des cosinus :

Pour que vous puissiez voir exactement comment les limites trigonométriques sont calculées, nous avons élaboré ci-dessous un exemple étape par étape.

Exemple de limite trigonométrique

Voyons comment une limite trigonométrique est résolue à l’aide de l’exemple suivant :

En essayant de calculer la limite trigonométrique, on obtient l’indétermination de zéro entre zéro :

➤ Voir : zéro limites entre zéro

Il faut donc transformer la fonction trigonométrique pour résoudre la limite. La fonction tangente est égale au sinus divisé par le cosinus, donc :

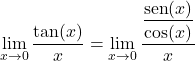
Nous pouvons maintenant exprimer la fonction sous forme de produit en appliquant les propriétés des fractions :

En utilisant les propriétés des limites, nous pouvons convertir la limite de deux fonctions multipliées en produit de deux limites :

Comme nous l’avons montré plus haut, la première limite trigonométrique donne 1 :

Il suffit donc de faire le calcul suivant :

Exercices résolus sur les limites trigonométriques

Exercice 1

Résolvez la limite trigonométrique suivante :

Tout d’abord, nous essayons de calculer la limite trigonométrique par évaluation directe :

Mais nous obtenons l’indétermination zéro sur zéro. Nous devons donc appliquer des transformations à la fonction.

Tout d’abord, nous ne laisserons que le x au dénominateur en procédant comme suit :

Maintenant, nous multiplions et divisons la fraction par 4 pour obtenir une expression avec laquelle la première formule des limites trigonométriques peut être appliquée :

Enfin, on applique la formule vue au début et on résout la limite trigonométrique :

Exercice 2

Calculez la limite trigonométrique suivante :

Tout d’abord, on essaie de trouver la limite trigonométrique :

Mais la forme indéterminée zéro correspond à zéro est atteinte.

Ensuite, on convertit la tangente en quotient du sinus et du cosinus :

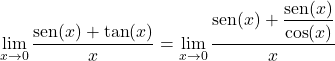
On multiplie et divise par le cosinus de x :

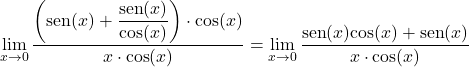
On prend un facteur commun au numérateur et on sépare la limite trigonométrique en deux :

Et enfin, on retrouve le résultat de la limite trigonométrique :

Exercice 3

Résolvez la limite de la fonction trigonométrique suivante lorsque x tend vers zéro :

En faisant le calcul direct on obtient la limite indéterminée 0 entre 0 :

Ainsi, nous simplifierons la limite en divisant chaque terme par la tangente de x :

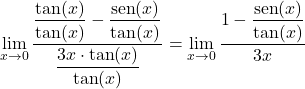
Deuxièmement, on peut déduire de l’identité trigonométrique fondamentale que la fraction du numérateur est équivalente au cosinus de x :

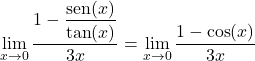
Et en appliquant la deuxième formule démontrée dans la théorie des limites trigonométriques, nous pouvons facilement résoudre la limite :

Exercice 4

Déterminer la solution de la limite trigonométrique suivante au point x=0 :

Si nous essayons de résoudre la limite, nous trouvons la forme indéterminée 0/0 :

L’expression algébrique du numérateur peut être réécrite en utilisant l’identité trigonométrique du sinus d’un angle double :

Séparons maintenant la limite de la fonction trigonométrique en un produit :

Et, pour finir, on résout la limite trigonométrique en appliquant les propriétés des limites :