▷ Risolvi l'indeterminazione zero tra zero (0/0)

In questo articolo spieghiamo come salvare il limite di una funzione quando dà incertezza 0/0. Inoltre, potrai esercitarti con esercizi risolti sull’indeterminazione dello zero tra zero.

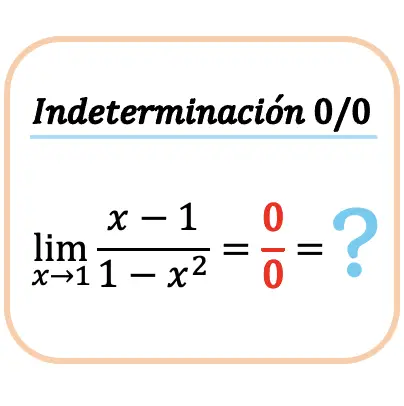
Come risolvere l’indeterminazione zero tra zero (0/0)

Vedremo poi come calcolare il limite di una funzione quando dà zero indeterminazione compresa tra zero (0/0). Per fare ciò, calcoleremo un esempio passo dopo passo:

$\displaystyle\lim_{x \to 2} \frac{x^2-x-2}{x^2-3x+2}$

Proviamo innanzitutto a calcolare il limite sostituendo il valore di x nella funzione:

$\displaystyle\lim_{x \to 2} \frac{x^2 - x -2}{x^2-3x+2}=\frac{2^2 -2-2}{2^2-3\cdot 2+2}=\frac{0}{0}$

Ma otteniamo l’indeterminazione 0 divisa per 0.

Quando il limite di una funzione puntuale dà l’ incertezza 0/0 , è necessario fattorizzare i polinomi del numeratore e del denominatore quindi semplificare i fattori comuni.

Dobbiamo quindi fattorizzare i polinomi del numeratore e del denominatore della frazione. Per fare ciò utilizziamo la regola di Ruffini:

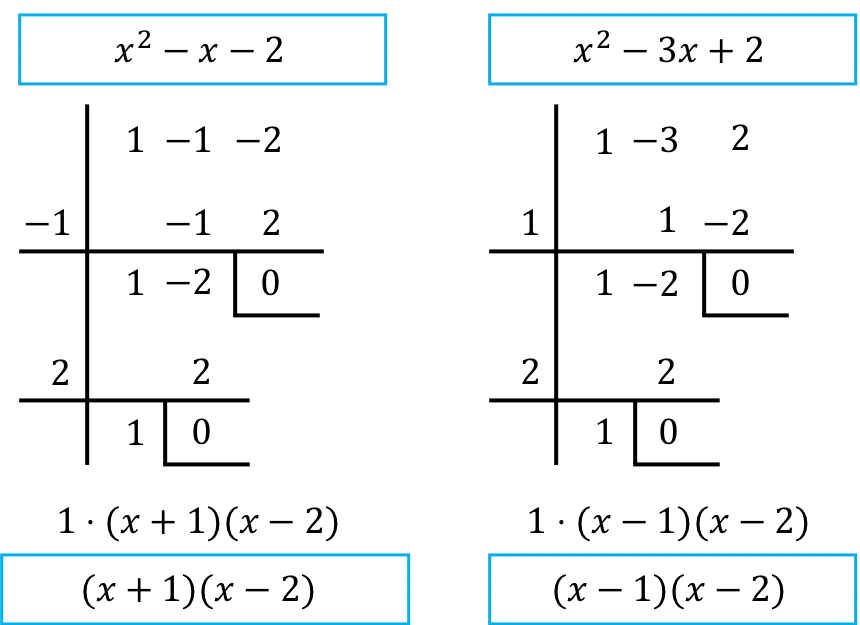
➤ Se non sai come fattorizzare un polinomio , ti consigliamo di consultare la spiegazione sul nostro sito specializzato in polinomi: www.polinomios.org

Pertanto, una volta fattorizzati i polinomi, il limite è il seguente:

$\displaystyle\lim_{x \to 2} \cfrac{x^2-x-2}{x^2-3x+2}=\lim_{x \to 2}\frac{(x+1)(x-2)}{(x-1)(x-2)}$

Possiamo ora semplificare il limite eliminando i fattori che si ripetono nel numeratore e nel denominatore della frazione:

$\displaystyle\lim_{x \to 2} \cfrac{(x+1)\cancel{(x-2)}}{(x-1)\cancel{(x-2)}}=\lim_{x \to 2} \cfrac{(x+1)}{(x-1)}$

E infine, ricalcoliamo il limite:

$\displaystyle\lim_{x \to 2} \cfrac{x+1}{x-1}=\cfrac{2+1}{2-1}=\cfrac{3}{1}=\bm{3}$

Come puoi vedere, una volta fattorizzati e semplificati i polinomi, è molto facile trovare la soluzione nel limite.

Indeterminazione 0/0 con radici

Abbiamo appena visto come si risolvono le indeterminazioni 0/0 delle funzioni razionali. Tuttavia, se il limite è di una funzione irrazionale (o radicale), l’indeterminazione 0/0 viene risolta diversamente.

$\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}$

Per prima cosa proviamo a risolvere il limite eseguendo le seguenti operazioni:

$\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}=\frac{1-1}{\sqrt{1}-1}=\frac{0}{0}$

Ma otteniamo zero su zero indeterminatezza.

Se il limite di una funzione con radici dà indeterminazione 0/0 , devi moltiplicare il numeratore e il denominatore della frazione per il coniugato dell’espressione radicale.

➤ Ricorda che il coniugato è la stessa espressione irrazionale ma con il segno centrale modificato.

Successivamente, moltiplichiamo sia il numeratore che il denominatore della frazione per il coniugato dell’espressione radicale:

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}$

Entro questo tipo di limiti, eseguendo questo passaggio otterremo sempre un’identità notevole che possiamo semplificare. In questo caso al denominatore abbiamo il prodotto di una somma e una differenza, quindi:

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}\right)^2-1^2}$

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{x-1}$

Semplifichiamo il fattore che si ripete al numeratore e al denominatore:

$\displaystyle\lim_{x \to 1} \frac{\cancel{\left(x-1\right)}\cdot\left(\sqrt{x}+1\right)}{\cancel{x-1}}=\lim_{x \to 1}\left(\sqrt{x}+1\right)$

E in questo modo possiamo trovare il risultato del limite:

$\displaystyle\lim_{x \to 1}\left(\sqrt{x}+1\right)=\sqrt{1}+1=2$

Esercizi risolti sull’indeterminazione 0/0

Di seguito abbiamo preparato diversi esercizi risolti passo passo sui limiti di funzioni che danno indeterminazioni 0/0. Puoi provare a farli e poi controllare la soluzione.

Non dimenticare che puoi farci qualsiasi domanda sulla risoluzione dei limiti nei commenti!

Esercizio 1

Calcola il limite della seguente funzione razionale nel punto x=-2.

$\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}$

Vedi la soluzione

Logicamente, proviamo prima a risolvere il limite:

$\displaystyle\lim_{x \to -2} \frac{x^2 +2x}{x^2-x-6}=\frac{(-2)^2+2\cdot (-2)}{(-2)^2-(-2)-6}=\frac{4-4}{4+2-6}=\frac{0}{0}$

Ma ci ritroveremo con un’indeterminatezza 0/0. Dobbiamo quindi fattorizzare i polinomi del numeratore e del denominatore:

$\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}=\lim_{x \to -2}\frac{x(x+2)}{(x+2)(x-3)}$

Ora semplifichiamo la frazione eliminando le parentesi che si ripetono al numeratore e al denominatore:

$\displaystyle\lim_{x \to -2}\frac{x\cancel{(x+2)}}{\cancel{(x+2)}(x-3)}=\lim_{x \to -2}\frac{x}{x-3}$

E infine ricalcoliamo il limite con la frazione semplificata:

$\displaystyle\lim_{x \to -2}\frac{x}{x-3}=\cfrac{-2}{-2-3}=\cfrac{-2}{-5}=\mathbf{\cfrac{2}{5}}$

Esercizio 2

Risolvi il limite della seguente funzione quando x si avvicina a -1:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}$

Vedi la soluzione

Per prima cosa proviamo a risolvere il limite come al solito:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3-5(-1)^2+2(-1)+8} =\frac{0}{0}$

Ma otteniamo l’indeterminazione 0 tra 0. Dobbiamo quindi fattorizzare i 2 polinomi della frazione:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)(x-2)(x-4)}$

Possiamo ora semplificare i polinomi:

$\displaystyle\lim_{x \to -1}\frac{(x-1)\cancel{(x+1)}(x+2)}{\cancel{(x+1)}(x-2)(x-4)}=\lim_{x \to -1}\frac{(x-1)(x+2)}{(x-2)(x-4)}$

E risolviamo il limite:

$\displaystyle\lim_{x \to -1} \frac{(x-1)(x+2)}{(x-2)(x-4)}=\frac{ (-1-1)(-1+2)}{(-1-2)(-1-4)}=\frac{(-2)\cdot (1)}{(-3)\cdot (-5)}=\frac{\bm{-2}}{\bm{15}}$

Esercizio 3

Determinare la soluzione del limite della seguente funzione radicale:

$\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}$

Vedi la soluzione

Innanzitutto controlliamo se il limite presenta qualche tipo di indeterminazione:

$\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}=\frac{2^2-3\cdot2+2}{2-\sqrt{2\cdot 2}}=\frac{4-6+2}{2-2}=\frac{0}{0}$

Il limite dà l’indeterminazione zero diviso zero e abbiamo una radice nella funzione. Dobbiamo quindi moltiplicare numeratore e denominatore della frazione per il coniugato dell’espressione radicale:

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{\left(2-\sqrt{2x}\right)\cdot \left(2+\sqrt{2x}\right)}$

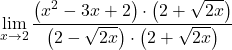
Il denominatore corrisponde allo sviluppo dell’identità notevole del prodotto di una somma e di una differenza, possiamo quindi semplificarlo:

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{2^2-\left(\sqrt{2x}\right)^2}$

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}$

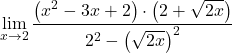
Tuttavia non possiamo ancora semplificare i termini della frazione. Dobbiamo quindi fattorizzare i polinomi:

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}=\lim_{x\to 2}\frac{(x-1)(x-2)\cdot\left(2+\sqrt{2x}\right)}{-2(x-2)}$

In questo modo possiamo semplificare la frazione:

$\displaystyle\lim_{x\to 2}\frac{(x-1)\cancel{(x-2)}\left(2+\sqrt{2x}\right)}{-2\cancel{(x-2)}}=\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}$

E ora possiamo determinare il risultato del limite:

$\displaystyle\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}=\frac{(2-1)\left(2+\sqrt{2\cdot 2}\right)}{-2}=\frac{1\cdot (2+2)}{-2}=\bm{-2}$

Esercizio 4

Calcolare il limite per x che tende a 0 della seguente funzione radicale:

$\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}$

Vedi la soluzione

Per prima cosa proviamo a calcolare il limite della funzione come facciamo sempre:

$\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}=\frac{0+0}{3-\sqrt{4\cdot 0+9}}=\frac{0}{3-3}=\frac{0}{0}$

Ma otteniamo la forma indeterminata di 0/0. Pertanto, moltiplichiamo il numeratore e il denominatore della funzione per il coniugato dell’espressione irrazionale:

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{\left(3-\sqrt{4x+9}\right)\cdot\left(3+\sqrt{4x+9}\right)}$

Applichiamo la corrispondente formula dell’identità notevole per semplificare il denominatore:

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{3^2-\left(\sqrt{4x+9}\right)^2}$

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{9-(4x+9)}$

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}$

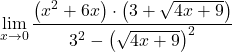
Ora fattorizziamo il binomio del numeratore prendendo il fattore comune:

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}=\lim_{x\to 0}\frac{\bigl[x(x+6)\bigr]\cdot\left(3+\sqrt{4x+9}\right)}{-4x}$

Semplifichiamo i fattori che si ripetono al numeratore e al denominatore della funzione:

$\displaystyle\lim_{x\to 0}\frac{\cancel{x}\left(x+6\right)\left(3+\sqrt{4x+9}\right)}{-4\cancel{x}}=\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}$

E, infine, risolviamo il limite della funzione:

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{(0+6)\left(3+\sqrt{4\cdot 0+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{6\cdot (3+3)}{-4}=\frac{36}{-4}=\bm{-9}\end{array}$

Esercizio 5

Risolvi il seguente limite utilizzando il metodo di indeterminazione 0/0:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}$

➤ Vedi: come calcolare i limiti laterali di una funzione

Vedi la soluzione

Proviamo innanzitutto a risolvere il limite:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3+5(-1)^2+7(-1)+3}=\frac{0}{0}$

Ma al limite otteniamo un’indeterminazione zero su zero. Pertanto, fattorizziamo i polinomi del numeratore e del denominatore:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)^2(x+3)}$

Ora semplifichiamo la frazione eliminando i fattori che si ripetono al numeratore e al denominatore:

$\displaystyle\lim_{x \to -1} \cfrac{(x-1)\cancel{(x+1)}(x+2)}{(x+1)^{\cancel{2}}(x+3)}=\lim_{x \to -1}\cfrac{(x-1)(x+2)}{(x+1)(x+3)}$

E calcoliamo nuovamente il limite:

$\displaystyle\lim_{x \to -1}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)(-1+2)}{(-1+1)(-1+3)}=\frac{-2\cdot 1}{0 \cdot 2}=\frac{-2}{0} =\infty$

Ma ora ci troviamo con l’indeterminatezza di un numero diviso 0. Dobbiamo quindi calcolare i limiti laterali della funzione quando x tende a -1.

Risolviamo innanzitutto il limite laterale della funzione nel punto x=-1 a sinistra:

$\displaystyle\lim_{x \to -1^{-}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{-0}=+\infty$

E poi calcoliamo il limite laterale della funzione nel punto x=-1 a destra:

$\displaystyle\lim_{x \to -1^{+}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{+0}=-\infty$

Pertanto, poiché i due limiti laterali non coincidono, il limite della funzione in x=-1 non esiste:

$\displaystyle\displaystyle \lim_{x \to -1^-}f(x)= +\infty\neq\lim_{x \to -1^+}f(x)=-\infty\ \bm{\longrightarrow} \ \cancel{\exists} \lim_{x \to -1} f(x)$

Indeterminazione zero tra zero (0/0)

Come risolvere l’indeterminazione zero tra zero (0/0)

Indeterminazione 0/0 con radici

Esercizi risolti sull’indeterminazione 0/0

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Lascia un commento Annulla risposta