Vettori perpendicolari o ortogonali

In questa pagina troverai tutto sui vettori perpendicolari (o ortogonali): cosa sono, quando due vettori sono ortogonali, come trovare un vettore perpendicolare a un altro, le proprietà dei vettori perpendicolari,… Inoltre, potrai vedere numerosi esempi ed esercizi risolti per vettori perpendicolari o ortogonali.

Cosa sono due vettori perpendicolari o ortogonali?

In matematica, due vettori sono ortogonali (o perpendicolari ) quando formano tra loro un angolo retto (90º).

Nel grafico seguente puoi vedere due vettori perpendicolari:

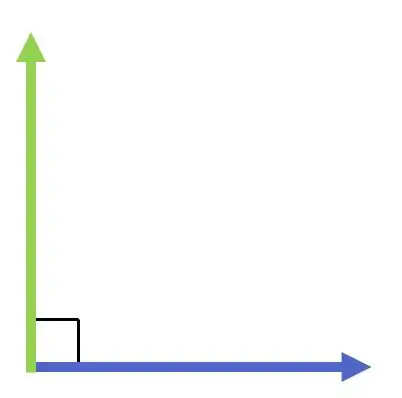
quando due vettori si dicono perpendicolari o ortogonali

D’altra parte, la perpendicolarità di due vettori dipende solo dalla loro direzione, e non dal loro modulo (o grandezza) o, ovviamente, dalla loro direzione. Cioè, due vettori saranno perpendicolari se formano un angolo di 90 gradi, indipendentemente dal fatto che abbiano o meno la stessa lunghezza.

Come faccio a sapere se due vettori sono ortogonali o perpendicolari?

Come abbiamo appena visto, graficamente è molto semplice vedere se due vettori sono perpendicolari. Tuttavia, puoi anche determinare se due vettori sono ortogonali senza rappresentarli graficamente:

Numericamente, due vettori sono ortogonali o perpendicolari quando il loro prodotto scalare è zero (0).

Ad esempio, mostreremo che i seguenti due vettori sono perpendicolari senza rappresentarli graficamente:

$\vv{\text{u}}=(3,2) \qquad\vv{\text{v}}=(-2,3)$

Per verificare che si tratti di vettori perpendicolari (o ortogonali), applichiamo la formula del prodotto scalare :

$\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(3,2)\cdot (-2,3) \\[1.5ex]&=3\cdot (-2) + 2 \cdot 3 \\[1.5ex] & = -6+6 \\[1.5ex] & =\bm{0} \end{aligned}$

Il risultato del prodotto scalare dei due vettori è zero, quindi si tratta di due vettori ortogonali (o perpendicolari) tra loro.

$\vv{\text{u}}\bm{\perp} \vv{\text{v}}$

Si noti che due vettori sono indicati come perpendicolari dal simbolo

$\bm{\perp}}.$

Pertanto, il prodotto scalare tra due vettori perpendicolari è zero. Tuttavia, il prodotto vettoriale di due vettori (un altro tipo di moltiplicazione tra vettori) dà il contrario: un vettore perpendicolare agli altri due. Pertanto è importante sapere come distinguere i due tipi di operazioni, puoi vedere le differenze tra loro nelle proprietà del prodotto incrociato .

Come si calcola un vettore perpendicolare o ortogonale ad un altro?

Il modo più semplice per calcolare un vettore perpendicolare a un altro nel piano (in R2) è intercalare le due coordinate del vettore e cambiare anche il segno in uno.

E per ottenere un vettore perpendicolare ad un altro nello spazio (in R3) è necessario interporre tra loro due coordinate, poi cambiare il segno di una di esse e, infine, azzerare la coordinata rimanente.

Affinché tu possa vedere le differenze nel calcolo di un vettore ortogonale rispetto a un altro a seconda che abbiano 2 o 3 coordinate, risolveremo un esercizio con ciascun tipo di vettore.

Trova un vettore perpendicolare o ortogonale nel piano cartesiano

Determinare un vettore perpendicolare al seguente vettore bidimensionale:

$\vv{\text{v}}=(4,1)$

Trattandosi di un vettore con due sole componenti, per ottenere un vettore perpendicolare è necessario alternare le sue componenti e negarne una:

$\vv{\mathbf{u}}\bm{=(-1,4)}$

Possiamo verificare dalla formula del prodotto scalare che questi sono effettivamente vettori perpendicolari:

$\vv{\text{v}} \cdot \vv{\text{u}}=(4,1)\cdot (-1,4) =0$

$\vv{\text{v}}\bm{\perp} \vv{\text{u}}$

Determinare un vettore perpendicolare o ortogonale nello spazio cartesiano

Calcolare un vettore ortogonale al seguente vettore tridimensionale:

$\vv{\text{v}}=(2,3,-1)$

In questo caso abbiamo un vettore a tre componenti, quindi per ottenere un vettore perpendicolare dobbiamo alternare due delle sue componenti, cambiare il segno di una di esse e convertire la coordinata rimanente in zero:

$\vv{\mathbf{u}}\bm{=(3,-2,0)}$

Possiamo verificare con la formula del prodotto scalare che questi sono effettivamente vettori ortogonali:

$\vv{\text{v}} \cdot \vv{\text{u}}=(2,3,-1)\cdot (3,-2,0) =0$

$\vv{\text{v}}\bm{\perp} \vv{\text{u}}$

Proprietà dei vettori perpendicolari e ortogonali

I vettori perpendicolari hanno le seguenti caratteristiche:

Relazione simmetrica : se un vettore è perpendicolare a un altro vettore, anche questo vettore è perpendicolare al primo vettore.

$\vv{\text{u}} \bm{\perp} \vv{\text{v}} \ \longrightarrow \ \vv{\text{v}} \bm{\perp} \vv{\text{u}}$

Proprietà irriflessiva : ovviamente nessun vettore può essere perpendicolare a se stesso.

$\vv{\text{v}} \ \cancel{\bm{\perp}}} \ \vv{\text{v}}$

Nella geometria euclidea (in R2), qualsiasi coppia di vettori perpendicolari ad un terzo vettore deve necessariamente essere parallela. Cioè, se un vettore è perpendicolare a un altro vettore e quel vettore è anche perpendicolare a un terzo vettore, il primo e l’ultimo vettore sono paralleli. Ciò è dovuto al quinto postulato di Euclide .

D’altronde dovete anche sapere che grazie a queste proprietà è possibile utilizzare il regolo del cavatappi. Questa tecnica semplifica il calcolo di un tipo di operazione vettoriale che, senza questa regola, richiederebbe molto tempo per essere risolta. Puoi vedere di cosa si tratta cliccando sulla spiegazione della regola del cavatappi .

Concetti relativi ai vettori perpendicolari o ortogonali

Esistono due tipi di vettori molto vicini ai vettori perpendicolari: vettori normali e vettori ortomarli. Sebbene siano tutti collegati tra loro, vogliamo chiarire in cosa differiscono per evitare ogni possibile confusione.

Un vettore normale è un vettore perpendicolare a un piano. Può quindi rientrare anche nel concetto di ortogonalità di un vettore, ma in questo caso è perpendicolare ad un piano anziché ad un altro vettore.

Due vettori ortonormali invece sono due vettori tra loro ortogonali che, per di più, sono vettori unitari (di grandezza pari a 1).

Infine, va anche notato che è molto comune utilizzare basi ortogonali (basi vettoriali formate da vettori perpendicolari tra loro) e anche basi ortonormali . Infatti il sistema di riferimento cartesiano è una base ortonormale.