Tutti i vettori linearmente indipendenti e dipendenti

In questa pagina spieghiamo cosa sono i vettori linearmente indipendenti e linearmente dipendenti. Vedrai anche esempi su come determinare se un insieme di vettori è linearmente dipendente o indipendente. E, inoltre, troverai esercizi e problemi risolti passo dopo passo sull’indipendenza e dipendenza lineare.

Cosa sono i vettori linearmente indipendenti?

Un insieme di vettori liberi è linearmente indipendente se nessuno di essi può essere scritto come combinazione lineare degli altri.

In altre parole, dato un insieme di vettori

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$

Questi sono linearmente indipendenti se l’unica soluzione della seguente equazione:

$a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n=0$

Questi sono tutti i coefficienti

$a_i$

uguale a 0:

$a_1=a_2=\dots = a_n=0$

Dal punto di vista geometrico, due vettori sono linearmente indipendenti se non hanno la stessa direzione, cioè se non sono paralleli.

Per brevità, a volte diciamo direttamente che sono vettori LI. Oppure che i vettori abbiano indipendenza lineare.

Cosa sono i vettori linearmente dipendenti?

Ovviamente, vettori linearmente dipendenti significano l’opposto di vettori linearmente indipendenti. La sua definizione è quindi:

Un insieme di vettori liberi del piano è linearmente dipendente se qualcuno di essi può essere espresso come combinazione lineare di altri vettori che compongono il sistema.

In altre parole, dato un insieme di vettori

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$

Questi sono linearmente dipendenti se esiste una soluzione alla seguente equazione:

$a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n=0$

in cui ha un certo coefficiente

$a_i$

è diverso da 0:

$a_i\neq 0$

È vero anche il contrario: se un vettore è una combinazione lineare di altri vettori, allora tutti i vettori dell’insieme sono linearmente dipendenti.

Inoltre, se due vettori sono paralleli, ciò implica che sono linearmente dipendenti.

A volte sono anche abbreviati e chiamati semplicemente vettori LD. O anche che i vettori abbiano una dipendenza lineare.

Esempio di come sapere se i vettori sono linearmente dipendenti o indipendenti

Vedremo poi un tipico esempio di vettori linearmente dipendenti e indipendenti.

Determina se i seguenti 3 vettori tridimensionali hanno dipendenza o indipendenza lineare:

$\vv{\text{u}} = (1,5,2)$

$\vv{\text{v}} = (-2,3,-1)$

$\vv{\text{w}} = (4,2,1)$

Innanzitutto dobbiamo enunciare la condizione di combinazione lineare:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

Ora sostituiamo ogni vettore con le sue coordinate. Come zero, che corrisponde al vettore zero:

$a_1(1,5,2)+a_2(-2,3,-1)+ a_3(4,2,1)=(0,0,0)$

I coefficienti moltiplicano i vettori, quindi la seguente espressione è equivalente:

$(a_1,5a_1,2a_1)+(-2a_2,3a_2,-a_2) + (4a_3,2a_3,a_3)=(0,0,0)$

Aggiungiamo i vettori:

$(a_1-2a_2+4a_3 \ , \ 5a_1+3a_2+2a_3 \ , \ 2a_1-a_2+a_3)=(0,0,0)$

Se guardiamo da vicino, l’espressione precedente corrisponde a 3 equazioni, poiché ciascuna coordinata del vettore sinistro deve essere uguale a ciascuna coordinata del vettore destro. Abbiamo quindi un sistema omogeneo di 3 equazioni in 3 incognite:

$\left. \begin{array}{l} a_1-2a_2+4a_3 = 0 \\[2ex] 5a_1+3a_2+2a_3 =0\\[2ex] 2a_1-a_2+a_3 = 0 \end{array} \right\}$

Quindi l’unica cosa che dobbiamo fare è risolvere il sistema di equazioni le cui incognite sono

$a_1, a_2$

$a_3.$

Per fare ciò, puoi utilizzare qualsiasi metodo (metodo di sostituzione, metodo di Gaus, regola di Cramer, ecc.). Tuttavia per sapere se i vettori sono LI o LD è sufficiente determinare se esiste una soluzione diversa da quella banale (tutti i coefficienti uguali a zero). COSÌ:

Se il determinante della matrice composta dalle componenti dei vettori è diverso da zero, ciò significa che il sistema di equazioni ha una sola soluzione (
$a_1=a_2=a_3=\dots=0$

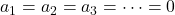
) e, quindi, i vettori sono linearmente indipendenti
Se invece il determinante della matrice composta dalle componenti dei vettori è uguale a zero, ciò implica che il sistema di equazioni ha più soluzioni e, quindi, i vettori sono linearmente dipendenti .

Quindi l’unica cosa da calcolare è il determinante con le coordinate dei vettori (essendo un determinante 3×3, si risolve con la regola di Sarrus). Questo determinante corrisponde ai coefficienti del precedente sistema di equazioni:

$\displaystyle \begin{vmatrix} 1&-2&4\\[1.1ex] 5&3&2 \\[1.1ex] 2&-1&1 \end{vmatrix} = -37 \bm{\neq 0}$

In questo caso il determinante è diverso da 0, quindi i vettori sono linearmente indipendenti .

Pertanto, l’unica soluzione possibile del sistema di equazioni è la soluzione banale con tutte le incognite pari a zero:

$a_1=a_2=a_3=0$

Proprietà dei vettori linearmente dipendenti e indipendenti

La dipendenza o indipendenza lineare dei vettori ha le seguenti caratteristiche:

Due vettori proporzionali sono paralleli e quindi linearmente dipendenti perché hanno la stessa direzione.

Allo stesso modo, se due vettori non hanno la stessa direzione o non sono proporzionali, sono linearmente indipendenti.

Tre vettori complanari (che si trovano sullo stesso piano) sono linearmente indipendenti.

Il vettore nullo
$(\vv{\text{v}}=(0,0,0))$

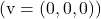
dipende linearmente da qualsiasi vettore.

Un insieme di vettori linearmente indipendenti genera uno spazio vettoriale e forma una base vettoriale. Se i tre vettori sono perpendicolari la base è ortogonale. E se anche il suo modulo è uguale a 1, ciò corrisponde a una base ortonormale.

Risolti esercizi di dipendenza lineare e indipendenza

Di seguito sono riportati diversi esercizi risolti su vettori linearmente dipendenti e indipendenti con cui esercitarsi.

Esercizio 1

Determina se i seguenti vettori sono linearmente dipendenti o indipendenti:

$\vv{\text{u}} = (1,-2,1)$

$\vv{\text{v}} = (2,1,3)$

$\vv{\text{w}} = (5,-1,1)$

Vedi la soluzione

Poniamo innanzitutto la condizione di combinazione lineare:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

$a_1(1,-2,1)+a_2(2,1,3)+ a_3(5,-1,1)=(0,0,0)$

$(a_1,-2a_1,a_1)+(2a_2,a_2,3a_2) + (5a_3,-a_3,a_3)=(0,0,0)$

$(a_1+2a_2+5a_3 \ , \ -2a_1+a_2-a_3 \ , \ a_1+3a_2+a_3)=(0,0,0)$

L’uguaglianza precedente corrisponde al seguente sistema di equazioni lineari:

$\left. \begin{array}{l} a_1+2a_2+5a_3 = 0 \\[2ex] -2a_1+a_2-a_3 =0\\[2ex] a_1+3a_2+a_3 = 0 \end{array} \right\}$

Una volta enunciato il sistema di equazioni, risolviamo il determinante della matrice con i suoi termini:

$\displaystyle \begin{vmatrix} 1&2&5\\[1.1ex] -2&1&-1 \\[1.1ex] 1&3&1 \end{vmatrix} = -29 \bm{\neq 0}$

In questo caso il determinante è diverso da 0, quindi i tre vettori sono linearmente indipendenti tra loro.

Esercizio 2

Classificare i seguenti vettori come linearmente dipendenti o indipendenti:

$\vv{\text{u}} = (1,4,3)$

$\vv{\text{v}} = (-2,0,2)$

$\vv{\text{w}} = (3,-1,-4)$

Vedi la soluzione

Innanzitutto poniamo l’equazione della combinazione lineare:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

$a_1(1,4,3)+a_2(-2,0,2)+ a_3(3,-1,-4)=(0,0,0)$

$(a_1,4a_1,3a_1)+(-2a_2,0,2a_2) + (3a_3,-a_3,-4a_3)=(0,0,0)$

$(a_1-2a_2+3a_3 \ , \ 4a_1-a_3 \ , \ 3a_1+2a_2-4a_3)=(0,0,0)$

Dalla precedente uguaglianza si ottiene il seguente sistema omogeneo di equazioni:

$\left. \begin{array}{l} a_1-2a_2+3a_3= 0 \\[2ex] 4a_1-a_3 =0\\[2ex] 3a_1+2a_2-4a_3 = 0 \end{array} \right\}$

Una volta enunciato il sistema di equazioni, risolviamo il determinante della matrice con le coordinate dei vettori:

$\displaystyle \begin{vmatrix} 1&-2&3\\[1.1ex] 4&0&-1 \\[1.1ex] 3&2&-4 \end{vmatrix} \bm{= 0}$

In questo caso il determinante equivale a 0, quindi i tre vettori dipendono linearmente l’uno dall’altro.

Esercizio 3

Per i tre vettori seguenti, indicare quali coppie di vettori sono linearmente dipendenti e quali coppie sono linearmente indipendenti.

$\vv{\text{u}} = (1,2,-2) \qquad \vv{\text{v}} = (2,4,-3) \qquad \vv{\text{w}} = (-4,-8,6)$

Vedi la soluzione

Il modo più semplice per sapere se una coppia di vettori è linearmente dipendente o indipendente è verificare se sono proporzionali.

Per prima cosa controlliamo il vettore

$\vv{\text{u}}$

con il vettore

$\vv{\text{v}} :$

$\cfrac{1}{2} = \cfrac{2}{4} \neq \cfrac{-2}{-3} \ \longrightarrow \ \text{LI}$

In secondo luogo, controlliamo il vettore

$\vv{\text{u}}$

con il vettore

$\vv{\text{w}} :$

$\cfrac{1}{-4} = \cfrac{2}{-8} \neq \cfrac{-2}{6} \ \longrightarrow \ \text{LI}$

Infine, testiamo il vettore

$\vv{\text{v}}$

con il vettore

$\vv{\text{w}} :$

$\cfrac{2}{-4} = \cfrac{4}{-8} = \cfrac{-3}{6} = -\cfrac{1}{2} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \text{LD}$

Pertanto, l’unica coppia di vettori che dipende linearmente l’uno dall’altro è

$\vv{\text{v}}$

$\vv{\text{w}}.$

Inoltre il loro rapporto è il seguente:

$\vv{\text{v}}= -\cfrac{1}{2} \vv{\text{w}}$

O equivalente:

$\vv{\text{w}}= -2\vv{\text{v}}$

Le altre coppie di vettori invece sono linearmente indipendenti.

Esercizio 4

Studia la dipendenza lineare o l’indipendenza dei seguenti 4 vettori l’uno dall’altro:

$\vv{\text{u}} = (0,1,2)$

$\vv{\text{v}} = (-1,-2,0)$

$\vv{\text{w}} = (4,1,-1)$

$\vv{\text{x}} = (-2,-3,2)$

Vedi la soluzione

Poniamo innanzitutto la condizione di combinazione lineare:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}+a_4\vv{\text{x}}=0$

$a_1(0,1,2)+a_2(-1,-2,0)+ a_3(4,1,-1)+a_4(-2,-3,2)=(0,0,0)$

$(0,a_1,2a_1)+(-a_2,-2a_2,0) +(4a_3,a_3,-a_3)+(-2a_4,-3a_4,2a_4)=(0,0,0)$

$(-a_2+4a_3-2a_4\ , \ a_1-2a_2+a_3-3a_4 \ , \ 2a_1-a_3+2a_4)=(0,0,0)$

In questo caso abbiamo un sistema di 3 equazioni in 4 incognite:

$\left. \begin{array}{l} -a_2+4a_3-2a_4 = 0 \\[2ex] a_1-2a_2+a_3-3a_4 =0\\[2ex] 2a_1-a_3+2a_4 = 0 \end{array} \right\}$

Non possiamo risolvere il determinante dell’intero sistema di matrici, poiché è possibile determinare solo le matrici quadrate. Dobbiamo quindi calcolare tutte le possibili combinazioni dei determinanti 3×3 e vedere se uno di essi è uguale a 0, in tal caso i vettori saranno linearmente dipendenti, invece se tutti i determinanti sono diversi da 0 i 4 vettori saranno essere linearmente indipendenti.

Calcoliamo il determinante dei coefficienti

$a_1, a_2$

$a_3:$

$\displaystyle \begin{vmatrix} 0&-1&4\\[1.1ex] 1&-2&1 \\[1.1ex] 2&0&-1 \end{vmatrix} =13\bm{\neq 0}$

Il determinante dei primi 3 coefficienti (o dei primi 3 vettori) è diverso da zero. Quindi ora proviamo con il determinante dei coefficienti

$a_1, a_2$

$a_4:$

$\displaystyle \begin{vmatrix} 0&-1&-2\\[1.1ex] 1&-2&-3 \\[1.1ex] 2&0&2 \end{vmatrix} \bm{= 0}$

Abbiamo ottenuto un determinante nullo, quindi non è necessario calcolare gli altri determinanti perché sappiamo già che i 4 vettori sono linearmente dipendenti .