In questa pagina spieghiamo cos’è un trinomio quadrato perfetto e come si spiega. Inoltre, potrai vedere diversi esempi ed esercitarti passo dopo passo con esercizi di trinomio quadrato perfetto.
Cos’è un trinomio quadrato perfetto?
Ovviamente, prima di vedere il significato di un trinomio quadrato perfetto, devi sapere cosa sono i trinomi , quindi ti consiglio di dare un’occhiata a questa pagina collegata (dove è spiegato in dettaglio) prima di continuare.
Quindi, la definizione di trinomio quadrato perfetto è la seguente:
In matematica, un trinomio quadrato perfetto , noto anche come TCP , è il trinomio ottenuto elevando al quadrato un binomio.
Pertanto un trinomio quadrato perfetto è costituito da un polinomio con due quadrati perfetti e un altro termine che è il doppio prodotto delle basi di questi quadrati.

Come puoi vedere dalle due formule sopra, il trinomio quadrato perfetto si ottiene da due identità notevoli (o prodotti notevoli), motivo per cui è così importante. Nello specifico, un trinomio quadrato perfetto si trova quando si risolve il quadrato di un’addizione o il quadrato di una sottrazione .
Esempi di trinomio quadrato perfetto
Per finire di comprendere il concetto di trinomio quadrato perfetto, spiegheremo passo dopo passo 2 esempi:
Esempio 1
![]()
Questo esempio è un trinomio quadrato perfetto perché nella sua espressione algebrica ci sono due quadrati perfetti (cioè hanno una radice quadrata esatta), poiché
![]()
e 9 sono equivalenti a
![]()
e 3 elevati rispettivamente a due:
![]()
![]()
E ancora, l’ultimo termine rimasto del trinomio
![]()
Si ottiene moltiplicando tra loro le basi dei due quadrati precedenti e per 2:
![]()
Quindi tutta l’identità notevole completa in questo esercizio sarebbe:
![]()
Esempio 2
![]()
Anche quest’altro esempio è un trinomio quadrato perfetto perché sono soddisfatte le 3 condizioni necessarie: due termini corrispondono a due quadrati perfetti, e un altro termine è il risultato della moltiplicazione delle basi di questi quadrati tra loro e per 2.
![]()
![]()
![]()
In questo caso il trinomio quadrato perfetto ha un monomio negativo, corrisponde quindi allo sviluppo dell’uguaglianza notevole di una differenza quadrata:
![]()
Come fattorizzare un trinomio quadrato perfetto
In algebra, un problema molto comune è la fattorizzazione di un trinomio quadrato perfetto (PCT). Nel caso non sapessi cosa significa, fattorizzare un polinomio significa trasformare la sua espressione in un prodotto di fattori.
Pertanto, per fattorizzare questo tipo di trinomio algebrico è necessario rispettare le seguenti regole:
- Il trinomio deve avere due quadrati perfetti, che chiameremo
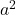
E
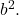
- Il terzo termine rimanente del trinomio deve essere uguale al doppio prodotto delle basi dei due quadrati perfetti, che corrisponde matematicamente all’espressione
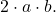
- Il trinomio scomposto sarà
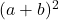
se tutti i termini del trinomio quadrato perfetto sono positivi, altrimenti, se il doppio prodotto delle basi dei quadrati ha segno negativo, il trinomio scomposto sarà
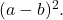
Per finire di comprendere la procedura, risolveremo un esercizio passo dopo passo:
- Fattorizza il seguente trinomio quadrato perfetto:
![]()
La prima cosa da fare è identificare se il trinomio ha due elementi che sono quadrati perfetti, o in altre parole, se la sua radice quadrata non dà un numero decimale. In questo problema
![]()
è il quadrato della variabile
![]()
e 36 è il quadrato di 6:
![]()
![]()
Il trinomio ha quindi due quadrati perfetti.
In secondo luogo dobbiamo verificare se il termine intermedio equivale al doppio prodotto delle due radici calcolato nel passaggio precedente:
![]()
Anche questa regola viene rispettata.
Allora tutte le condizioni sono soddisfatte. Pertanto, il trinomio quadrato perfetto fattorizzato è il binomio formato dalle due radici trovate (
![]()
e il numero 6) al quadrato:
![]()
Dato che il termine intermedio è negativo, dobbiamo mettere tra parentesi anche il segno meno. Se invece fosse positivo dovremmo aggiungere una somma:
![]()
Logicamente, la fattorizzazione è una procedura complicata quindi, oltre a provare a svolgere l’esercizio seguente, ti consiglio di guardare questi esempi di fattorizzazione di polinomi . In questo link spieghiamo anche un metodo che viene utilizzato non solo per fattorizzare i trinomi, ma anche qualsiasi tipo di polinomio, e altrettanto velocemente.
Esercizi risolti del trinomio quadrato perfetto
Trasforma i seguenti trinomi in binomi quadrati applicando la formula corrispondente:
![]()
![]()
![]()
![]()
![]()
Per convertire un trinomio quadrato perfetto nella potenza di un binomio quadrato, è necessario utilizzare le formule per le identità notevoli del quadrato di una somma e del quadrato di una differenza, che sono:
![]()
![]()
Ancora:
![]()
![]()
![]()
![]()
![]()
⬇⬇⬇ Non dimenticare che puoi scriverci tutte le tue domande qui sotto nei commenti! ⬇⬇⬇