▷ Come risolvere tutti i tipi di indeterminazioni (limiti)

In questo articolo spieghiamo cos’è l’indeterminazione. Scoprirai quali sono tutti i tipi di indeterminazioni e come risolverle. Inoltre potrai vedere esercizi risolti passo dopo passo sui limiti funzionali di tutte le indeterminazioni.

Cosa sono le indeterminazioni?

Le indeterminazioni, dette anche forme indeterminate, sono espressioni matematiche che compaiono nel calcolo dei limiti di funzioni il cui risultato non è definito. Pertanto, per risolvere le indeterminazioni dei limiti è necessario applicare una procedura preliminare che dipende dal tipo di funzione.

Cioè, quando si ottiene l’indeterminazione, non significa che il limite non esiste o che non può essere risolto, ma piuttosto che bisognerà apportare modifiche alla funzione per trovare la soluzione del limite.

Tipi di indeterminazioni

Le indeterminazioni, o forme indeterminate, sono classificate nei seguenti tipi:

Indeterminatezza infinito meno infinito (∞-∞)
Numero di indeterminazioni tra zero (k/∞)
Indeterminazione zero tra zero (0/0)
Indeterminazione infinita tra l’infinito (∞/∞)
Indeterminatezza 1 elevata all’infinito (1 ^∞ )
Indeterminatezza zero elevata a zero (0 ⁰ )
Indeterminazione zero per l’infinito (0·∞)
Indeterminazione zero elevata all’infinito (0 ^∞ )
Indeterminatezza infinita portata a zero (∞ ⁰ )

Vedremo poi come risolvere ogni tipo di indeterminazioni.

Infinito meno infinita indeterminatezza

La forma indeterminata infinito meno infinito non è uguale a zero, poiché sottraiamo due numeri molto grandi ma non sappiamo quale sia il maggiore. Il risultato della differenza degli infiniti dipende quindi dall’ordine di ciascun infinito.

$\infty-\infty$

Risolvere questo tipo di indeterminatezza non è semplice, perché a seconda del tipo di funzione occorre applicare una procedura o un’altra. Pertanto, ti consigliamo di visualizzare la spiegazione completa nel seguente link:

➤ Vedi: come risolvere l’indeterminazione infinito meno infinito

Numero di indeterminazioni compreso tra zero

L’ indeterminazione di una costante divisa per zero si ottiene quando si annulla il denominatore di una funzione razionale.

$\cfrac{k}{0}$

Il risultato di questo tipo di forma indeterminata sarà sempre più infinito, meno infinito oppure il limite della funzione non esisterà. Vediamo come viene calcolata questa indeterminazione risolvendo come esempio un limite:

$\displaystyle\lim_{x\to 0}\cfrac{-4}{x^2}=\cfrac{-4}{0^2}=\cfrac{-4}{0}=\infty$

Abbiamo ottenuto l’indeterminatezza di un numero diviso zero, quindi dobbiamo calcolare i limiti laterali della funzione:

$\displaystyle\lim_{x\to 0^-}\cfrac{-4}{0^2}=\cfrac{-4}{(-0,001)^2}=\cfrac{-4}{+0}=-\infty$

$\displaystyle\lim_{x\to 0^+}\cfrac{-4}{0^2}=\cfrac{-4}{0,001^2}=\cfrac{-4}{+0}=-\infty$

➤ Vedi: cosa sono i limiti laterali?

I due limiti laterali della funzione danno lo stesso risultato, quindi per definizione il limite della funzione quando x tende a 0 dà meno infinito:

$\displaystyle\lim_{x\to 0^-}f(x)=\lim_{x\to 0^+}f(x)=-\infty \ \longrightarrow \ \lim_{x\to 0}f(x)=-\infty$

Si noti che se i limiti laterali avessero dato valori diversi, il limite della funzione in questo punto non esisterebbe.

Zero tra zero indeterminatezza

Il limite indeterminato zero diviso zero è molto comune e si ottiene nelle funzioni con frazioni in cui numeratore e denominatore si annullano.

$\cfrac{0}{0}$

Questo tipo di limite indeterminato viene risolto in modo diverso a seconda della funzione. Ad esempio, se la funzione ha radici, è necessario eseguire passaggi diversi. Puoi vedere le diverse risoluzioni di questo tipo di indeterminatezza nel seguente link:

➤ Vedi: come risolvere l’indeterminazione dello zero tra zero

Infinita indeterminatezza tra gli infiniti

L’indeterminazione infinita tra l’infinito di solito si verifica nei limiti infiniti delle funzioni con frazioni. Sebbene l’indeterminazione sia il quoziente di due infiniti, il risultato non deve necessariamente essere infinito.

$\cfrac{\infty}{\infty}$

Questo tipo di forma indeterminata si risolve mediante confronto. Si osserva cioè il grado del numeratore e il grado del denominatore e, a seconda di quale sia maggiore, il risultato limite è l’uno o l’altro. Puoi vedere tutti i casi nel seguente link:

➤ Vedi: esercizi risolti sui limiti infiniti tra l’infinito

Indeterminatezza 1 elevata all’infinito

Matematicamente, si potrebbe pensare che 1 all’infinito dia 1, poiché qualsiasi potenza di 1 è uguale a 1. Tuttavia, questo termine è un’indeterminazione e, quindi, non è possibile dedurne il risultato così facilmente.

$1^{\infty}$

Questo tipo di indeterminazione si calcola applicando la seguente formula:

$\displaystyle\lim_{x\to+\infty}f(x)^{g(x)}=\lim_{x\to+\infty}e^{g(x)\cdot [f(x)-1]}$

Ad esempio, il seguente limite è indeterminato perché dà la potenza dell’infinito:

$\displaystyle\lim_{x\to+\infty}\left(1-\frac{1}{x}\right)^x=\left(1-\frac{1}{+\infty}\right)^{+\infty}=(1-0)^{+\infty}=1^{+\infty}$

Dobbiamo quindi utilizzare la formula per questo tipo di indeterminazione:

$\displaystyle\lim_{x\to+\infty}e^{x\cdot\left[1-\frac{1}{x}-1\right]}=\lim_{x\to+\infty}e^{x\cdot\left[-\frac{1}{x}\right]}=\lim_{x\to+\infty}e^{-1}=\frac{1}{e}$

E così abbiamo già risolto il limite indeterminato elevato all’infinito.

Zero indeterminatezza portata a zero

L’indeterminazione zero rispetto alla potenza zero appare entro i limiti delle funzioni complicate.

$0^0$

Per risolvere questo tipo di limite indeterminato, è necessario utilizzare la seguente proprietà limit:

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

Ad esempio, il seguente limite dà la forma indeterminata 0 alla potenza di 0:

$\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=\left(\frac{1}{+\infty}\right)^{\frac{1}{+\infty}}=0^0$

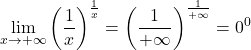
Ma se applichiamo i logaritmi al limite, possiamo trovare il suo valore:

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln\left(\frac{1}{x}\right)}}=\\[5ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln\left(\frac{1}{x}\right)}{x}}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln1-\ln x}{x}}}=\\[5ex]=\displaystyle e^{^{\displaystyle\lim_{x\to +\infty}\frac{-\ln x}{x}}}=e^{^{\displaystyle\frac{-\infty}{+\infty}}}=e^0=1\end{array}$

Indeterminazione zero per l’infinito

È difficile incontrare l’ indeterminatezza del prodotto tra zero e infinito , ma ciò non significa che sia facile da determinare.

$0\cdot \infty$

Non esiste un metodo unico per risolvere questo tipo di indeterminatezza, ma dipende dal tipo di funzione. In questo caso dobbiamo trasformare la funzione in indeterminatezza infinita divisa per infinito o indeterminatezza zero divisa per zero, e da lì applicare i metodi risolutivi che abbiamo visto sopra per ciascuna indeterminazione.

Quindi se il limite di una funzione è 0 e il limite dell’altra funzione è ∞:

$\displaystyle\lim_{x\to a}f(x)=0\qquad\lim_{x\to a}g(x)=\infty$

Possiamo trasformare questo tipo indefinitamente apportando le seguenti modifiche:

$\displaystyle\lim_{x\to a}f(x)\cdot g(x)\begin{cases}\displaystyle\lim_{x\to a}\frac{f(x)}{\displaystyle\frac{1}{g(x)}}=\frac{0}{0}\\[10ex]\displaystyle\lim_{x\to a}\frac{g(x)}{\displaystyle\frac{1}{f(x)}}=\frac{\infty}{\infty}\end{cases}$

Vediamo come fare risolvendo come esempio un limite indeterminato:

$\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=e^{-\infty}\cdot (+\infty)=0\cdot \infty$

Operiamo sulla funzione per ottenere un’indeterminazione infinita su infinito quindi troviamo il limite:

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=\lim_{x\to +\infty}\frac{x}{\displaystyle\frac{1}{e^{-x}}}=\\[6ex]=\displaystyle \lim_{x\to +\infty}\frac{x}{e^x}=\frac{+\infty}{e^{+\infty}}=\frac{+\infty}{+\infty}=0\end{array}$

Indeterminazione zero elevata all’infinito

Lo zero di indeterminazione elevato all’infinito è un po’ difficile da comprendere, poiché stiamo elevando un numero molto piccolo a un numero molto grande.

$0^{\infty}$

Quando si ottengono queste forme indeterminate, è necessario utilizzare la seguente formula:

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

Risolviamo un esempio per capire meglio come calcolare questo tipo di indeterminazione:

$\begin{array}{l}\displaystyle\lim_{x\to 0^+}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to 0^+}\frac{1}{x}\cdot \ln(x)}}=\\[3.5ex]\displaystyle =e^{^{\displaystyle\frac{1}{0^+}\cdot \ln(0^+)}}=e^{+\infty\cdot (-\infty)}\\[3ex]\displaystyle =e^{-\infty}=\frac{1}{e^{+\infty}}=0\end{array}$

Indeterminatezza infinita portata a zero

Normalmente, qualsiasi potenza elevata a zero dà 1, tuttavia, l’ indeterminatezza dell’infinito elevato a zero non deve necessariamente essere così.

$\infty^0$

Come nelle indeterminazioni zero elevato a zero e zero elevato all’infinito, per risolvere questo tipo di limite indeterminato è necessario applicare i logaritmi:

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

Vediamo come si risolve questo tipo di limiti indeterminati calcolando passo passo un esempio:

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln(x)}}=\\[3ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln(x)}{x}}}=e^{^{\displaystyle\frac{\ln(+\infty)}{+\infty}}}=\\[3ex]\displaystyle =e^{^{\displaystyle\frac{+\infty}{+\infty}}}=e^0=1\end{array}$

Tipi di indeterminazioni (limiti indeterminati)

Cosa sono le indeterminazioni?

Tipi di indeterminazioni

Infinito meno infinita indeterminatezza

Numero di indeterminazioni compreso tra zero

Zero tra zero indeterminatezza

Infinita indeterminatezza tra gli infiniti

Indeterminatezza 1 elevata all’infinito

Zero indeterminatezza portata a zero

Indeterminazione zero per l’infinito

Indeterminazione zero elevata all’infinito

Indeterminatezza infinita portata a zero

Lascia un commento Annulla risposta