In questo articolo troverai la definizione del teorema di Weierstrass. Inoltre, potrai esercitarti con diversi esercizi risolti passo dopo passo sul teorema di Weierstrass per capirlo perfettamente.
Enunciato del teorema di Weierstrass
Il teorema di Weierstrass dice che se una funzione è continua su un intervallo chiuso, quella funzione ha un massimo assoluto e un minimo assoluto su quell’intervallo.
➤ Vedi: Cos’è una funzione continua?
Il teorema di Weierstrass afferma solo che esiste un massimo e un minimo, ma non è utile calcolare i valori di questi punti.
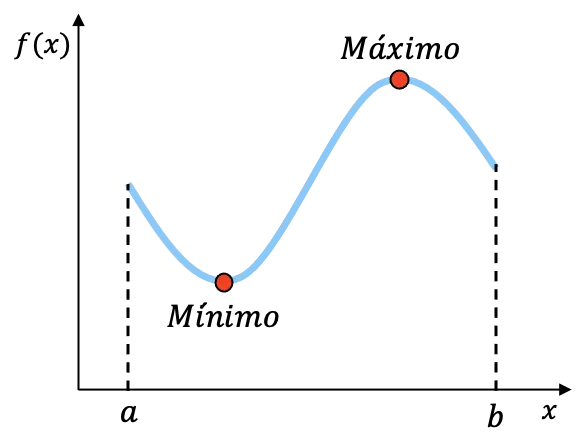
Ad esempio, la funzione rappresentata nel grafico sopra è continua sull’intervallo [a,b] e ha un minimo e un massimo su questo intervallo. Sebbene non possiamo conoscere le coordinate esatte di questi due punti, sappiamo che la funzione ha questi due punti finali nell’intervallo.
➤ Vedi: come calcolare il massimo e il minimo di una funzione
Poiché la funzione è continua su tutto l’intervallo, ciò significa che assumerà anche tutti i valori possibili compresi tra il minimo assoluto e il massimo assoluto in quello stesso intervallo.
Inoltre, come conseguenza del teorema di Weierstrass, si può dedurre che qualsiasi funzione continua su un intervallo chiuso è limitata sopra e sotto , e i limiti superiore e inferiore della funzione sono rispettivamente il massimo e il minimo assoluti.
Matematicamente, il teorema di Weierstrass può essere espresso come segue:
Oro
E
sono due punti inclusi (rispettivamente il minimo assoluto e il massimo assoluto) nell’intervallo chiuso
![[a,b]](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcda5ef4ae327e1afef79dc73df91703_l3.png "Rendered by QuickLaTeX.com")
in cui è definita la funzione.
La dimostrazione del teorema di Weierstrass è piuttosto complicata e non contribuisce molto al concetto, quindi non la spiegheremo in questo articolo. L’importante è che tu capisca cos’è il teorema di Weierstrass e a cosa serve.
Problemi risolti dal teorema di Weierstrass
Esercizio 1
Determina se la seguente funzione è limitata all’intervallo proposto:
![f(x)=\log_3(x-4) \qquad x \in [5,10]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e6a705ea1c5d586cf31d683ac7ccc85_l3.png "Rendered by QuickLaTeX.com")
➤ Vedi:dominio di una funzione logaritmica
Possiamo determinare se la funzione è limitata all’intervallo [5,10] applicando il teorema di Weierstrass. Dobbiamo quindi sapere se la funzione è continua in questo intervallo, per fare ciò calcoliamo il dominio della funzione logaritmica:
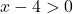
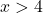
La funzione è continua per tutti i valori maggiori di x=4, quindi è continua nell’intervallo [5,10].
Pertanto, la funzione soddisfa il teorema di Weierstrass sull’intervallo [5,10], il che significa che è limitata sopra e sotto su questo intervallo.
Esercizio 2
Determina se la seguente funzione ha un massimo e/o un minimo nell’intervallo proposto:
![f(x)=\cfrac{3x^2-4}{2x-4} \qquad x \in [-3,3]](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f2e72f629bae2c39821ddbfbf6c93fc_l3.png "Rendered by QuickLaTeX.com")
➤ Vedi: dominio di una funzione razionale
Innanzitutto analizziamo la continuità della funzione razionale:
Tuttavia la funzione presenta una discontinuità in x=2, il che implica che non è continua nell’intervallo [-3,3].
In breve, la funzione non soddisfa il teorema di Weierstrass e quindi non possiamo dire se abbia un minimo o un massimo in questo intervallo.
Esercizio 3
Determina se la seguente funzione ha un massimo e/o un minimo nell’intervallo proposto e calcola questi punti:
![f(x)=x^2+3 \qquad x \in [0,4]](https://mathority.org/wp-content/ql-cache/quicklatex.com-4dd0cf4151f8b5c1b4e69be89b7a71e1_l3.png "Rendered by QuickLaTeX.com")
➤ Vedi: caratteristiche delle funzioni quadratiche
Il dominio di qualsiasi funzione quadratica è costituito da tutti i numeri reali:
La funzione è quindi continua sull’intervallo [0,4] e soddisfa il teorema di Weierstrass. La funzione quindi ha un minimo assoluto e un massimo assoluto su questo intervallo.
Inoltre, il vertice di questa parabola è esattamente in x=0, quindi la funzione è strettamente crescente sull’intervallo [0,4] e, di conseguenza, il minimo è in x=0 e il massimo in x= 4 .
Karl Weierstrass
Una volta visto cosa significa il teorema di Weierstrass, spiegheremo brevemente chi era l’inventario di questo teorema.
Karl Theodor Wilhelm Weierstrass fu un matematico tedesco molto importante del XIX secolo, più precisamente nacque il 31 ottobre 1815 a Ostenfelde e morì il 19 febbraio 1897 a Berlino.
Oltre al teorema di Weierstrass, è noto anche per altri suoi contributi alla matematica. Tra questi diede le definizioni di continuità, limite e derivata, tre concetti di funzione molto importanti.
Allo stesso modo riuscì a dimostrare alcuni teoremi che all’epoca non erano ancora matematicamente verificati, come il teorema di Bolzano-Weierstrass, il teorema del valore medio o il teorema di Heine-Borel.
Come curiosità, c’è un cratere lunare e un asteroide che porta il nome di Weierstrass in suo onore.