Teorema di Rouche-Frébenius

In questa pagina scopriremo cos’è il teorema di Rouché Frobenius e come con esso si calcola il rango di una matrice. Troverai anche esempi ed esercizi risolti passo passo con il teorema di Rouché-Frobenius.

Cos’è il teorema di Rouché-Frobenius?

Il teorema di Rouché-Frobenius è un metodo per classificare sistemi di equazioni lineari. In altre parole, il teorema di Rouché-Frobenius serve per scoprire quante soluzioni ha un sistema di equazioni senza doverlo risolvere.

Esistono 3 tipi di sistemi di equazioni:

Sistema compatibile determinato (SCD): il sistema ha una soluzione unica.
Sistema compatibile indeterminato (ICS): il sistema ha infinite soluzioni.
Sistema incompatibile (SI): il sistema non ha soluzione.

Inoltre, il teorema di Rouché-Frobenius consentirà successivamente di risolvere i sistemi utilizzando la regola di Cramer .

Enunciato del teorema di Rouché-Frobenius

Lo dice il teorema di Rouché-Frobenius

$\displaystyle \bm{A}$

è la matrice formata dai coefficienti delle incognite di un sistema di equazioni. e la pancia

$\displaystyle \bm{A'}$

, o matrice estesa , è la matrice formata dai coefficienti delle incognite di un sistema di equazioni e dai termini indipendenti:

Il teorema di Rouché-Frobenius ci permette di sapere con quale tipo di sistema di equazioni abbiamo a che fare a seconda del rango delle matrici A e A’:

Se rango(A) = rango(A’) = numero di incognite ⟶ Sistema compatibile determinato (SCD)
Se rango(A) = rango(A’) < numero di incognite ⟶ Sistema compatibile indeterminato (SCI)
se intervallo(A)
$\bm{\neq}$

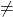
intervallo (A’) ⟶ Sistema incompatibile (SI)

Una volta che sappiamo cosa dice il teorema di Rouché-Frobenius, vedremo come risolvere gli esercizi del teorema di Rouché-Frobenius. Ecco 3 esempi: un esercizio risolto utilizzando il teorema di ogni tipo di sistema di equazioni.

Esempio di sistema compatibile determinato (SCD)

$\begin{cases} 2x+y-3z=0 \\[1.5ex] x+2y-z= 1 \\[1.5ex] 4x-2y+z = 3\end{cases}$

La matrice A e la matrice estesa A’ del sistema sono:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 1 & 2 & -1 & 1 \\[1.1ex] 4 & -2 & 1 & 3\end{array} \right)$

Calcoliamo ora il rango della matrice A. Per fare ciò controlliamo se il determinante dell’intera matrice è diverso da 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{vmatrix} = 25 \neq 0$

Poiché la matrice ha un determinante 3×3 diverso da 0, la matrice A ha rango 3:

$\displaystyle rg(A)=3$

Una volta conosciuto il rango di A, calcoliamo il rango di A’, che sarà almeno di rango 3 perché abbiamo appena visto che ha al suo interno un determinante di ordine 3 diverso da 0. Inoltre non può essere di rango 4, poiché non possiamo creare alcun determinante di ordine 4. Pertanto, anche la matrice A’ è di rango 3:

$\displaystyle rg(A')=3$

Pertanto, poiché il rango della matrice A è pari al rango della matrice A’ e al numero di incognite del sistema (3), sappiamo dal teorema di Rouché Frobenius che si tratta di un Sistema Determinato Compatibile (SCD) :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Esempio di sistema compatibile indeterminato (ICS)

$\begin{cases} x-y+2z=1 \\[1.5ex] 3x+2y+z= 5 \\[1.5ex] 2x+3y-z = 4\end{cases}$

La matrice A e la matrice estesa A’ del sistema sono:

$\displaystyle A= \left( \begin{array}{ccc} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & -1 & 2 & 1 \\[1.1ex] 3 & 2 & 1 & 5 \\[1.1ex] 2 & 3 & -1 & 4 \end{array} \right)$

Calcoliamo ora il rango della matrice A. Per fare ciò controlliamo se il determinante dell’intera matrice è diverso da 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{vmatrix} = 0$

Il determinante dell’intera matrice A dà 0, quindi non è di rango 3. Per vedere se è di rango 2, dobbiamo trovare una sottomatrice in A il cui determinante è diverso da 0. Ad esempio, quello dall’angolo in alto a sinistra :

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

Poiché la matrice ha un determinante 2×2 diverso da 0, la matrice A ha rango 2:

$\displaystyle rg(A)=2$

Una volta conosciuto il rango di A, calcoliamo il rango di A’. Sappiamo già che il determinante delle prime 3 colonne dà 0, quindi proviamo gli altri possibili determinanti 3×3:

$\displaystyle \begin{vmatrix}1 & -1 & 1 \\[1.1ex] 3 & 2 & 5 \\[1.1ex] 2 & 3 & 4\end{vmatrix} = 0 \quad \begin{vmatrix}1 & 2 & 1 \\[1.1ex] 3 & 1 & 5 \\[1.1ex] 2 & -1 & 4\end{vmatrix} = 0 \quad \begin{vmatrix} -1 & 2 & 1 \\[1.1ex] 2 & 1 & 5 \\[1.1ex] 3 & -1 & 4\end{vmatrix} = 0$

Tutti i determinanti 3×3 della matrice A’ sono 0, quindi neanche la matrice A’ sarà di rango 3. Tuttavia, al suo interno ha determinanti di ordine 2 diversi da 0. Ad esempio:

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

Quindi la matrice A’ sarà di rango 2 :

$\displaystyle rg(A')=2$

L’estensione della matrice A è uguale all’estensione della matrice A’ ma queste sono inferiori al numero di incognite del sistema (3). Pertanto, secondo il teorema di Rouché-Frobenius, si tratta di un sistema compatibile indeterminato (ICS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

Esempio di sistema incompatibile (IS)

$\begin{cases} 2x+y-2z=3 \\[1.5ex] 3x-2y+z= 2 \\[1.5ex] x+4-5z = 3 \end{cases}$

La matrice A e la matrice estesa A’ del sistema sono:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -2 & 3 \\[1.1ex] 3 & -2 & 1 & 2 \\[1.1ex] 1 & 4 & -5 & 3 \end{array} \right)$

Calcoliamo ora il rango della matrice A. Per fare ciò controlliamo se il determinante dell’intera matrice è diverso da 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & -2 \end{vmatrix} = -7 \neq 0$

Poiché la matrice ha un determinante di ordine 2 diverso da 0, la matrice A è di rango 2:

$\displaystyle rg(A)=2$

Una volta conosciuto il rango di A, calcoliamo il rango di A’. Sappiamo già che il determinante delle prime 3 colonne dà 0, quindi ora proviamo, ad esempio, con il determinante delle ultime 3 colonne:

$\displaystyle \begin{vmatrix} 1 & -2 & 3 \\[1.1ex] -2 & 1 & 2 \\[1.1ex] 4 & -5 & 3 \end{vmatrix} = 3 \neq 0$

D’altra parte, la matrice A’ contiene un determinante il cui risultato è diverso da 0, quindi la matrice A’ avrà rango 3 :

$\displaystyle rg(A')=3$

Pertanto, poiché il rango della matrice A è minore del rango della matrice A’, deduciamo dal teorema di Rouché-Frobenius che si tratta di un Sistema Incompatibile (SI) :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Problemi risolti del teorema di Rouché-Frobenius

Esercizio 1

Determina il tipo del seguente sistema di equazioni a 3 incognite utilizzando il teorema di Rouché-Frobenius:

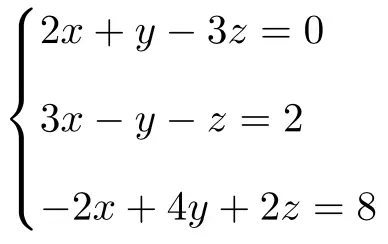
Esercizio risolto del teorema di Rouche - frobenius

vedi soluzione

Per prima cosa realizziamo la matrice A e la matrice estesa A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 3 & -1 & -1 & 2 \\[1.1ex] -2 & 4 & 2 & 8 \end{array} \right)$

Dobbiamo ora trovare il rango della matrice A. Per fare ciò controlliamo se il determinante della matrice è diverso da 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{vmatrix} = -4+2-36+6+8-6=-30 \bm{\neq 0}$

La matrice avente un determinante del terzo ordine diverso da 0, la matrice A ha rango 3:

$\displaystyle rg(A)=3$

Una volta conosciuto il rango di A, calcoliamo il rango di A’. Questo sarà almeno di rango 3, perché abbiamo appena visto che ha al suo interno un determinante di ordine 3 diverso da 0. Inoltre, non può essere di rango 4, poiché non possiamo non creare un determinante 4×4. Pertanto anche la matrice A’ è di rango 3:

$\displaystyle rg(A')=3$

Quindi, grazie al teorema di Rouché-Frobenius, sappiamo che si tratta di un determinato sistema compatibile (SCD), perché l’intervallo di A è uguale all’intervallo di A’ e al numero di incognite.

Esercizio 2

Classificare il seguente sistema di equazioni a 3 incognite utilizzando il teorema di Rouché-Frobenius:

vedi soluzione

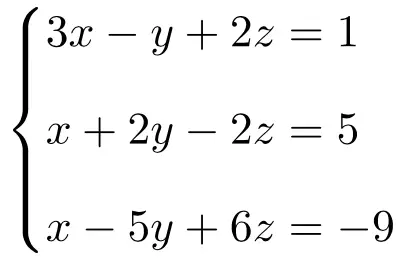
Costruiamo innanzitutto la matrice A e la matrice estesa A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc}3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -1 & 2 & 1 \\[1.1ex] 1 & 2 & -2 & 5 \\[1.1ex] 1 & -5 & 6 & -9 \end{array} \right)$

Ora calcoliamo l’intervallo della matrice A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 3 & -1 \\[1.1ex] 1 & 2 \end{vmatrix} = 7 \neq 0$

Quindi la matrice A ha rango 2:

$\displaystyle rg(A)=2$

Una volta conosciuto il rango di A, calcoliamo il rango di A’. Sappiamo già che il determinante delle prime 3 colonne dà 0, quindi proviamo gli altri possibili determinanti 3×3:

$\displaystyle \begin{vmatrix}-1 & 2 & 1 \\[1.1ex] 2 & -2 & 5 \\[1.1ex] -5 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix}3 & 2 & 1 \\[1.1ex] 1 & -2 & 5 \\[1.1ex] 1 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix} 3 & -1 & 1 \\[1.1ex] 1 & 2 & 5 \\[1.1ex] 1 & -5 & -9\end{vmatrix} = 0$

Tutti i determinanti 3×3 della matrice A’ sono 0, quindi neanche la matrice A’ sarà di rango 3. Tuttavia al suo interno ha molti determinanti di ordine 2 diversi da 0. Ad esempio:

$\displaystyle \begin{vmatrix} -1 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -2 \neq 0$

Quindi la matrice A’ sarà di rango 2 :

$\displaystyle rg(A')=2$

Il rango della matrice A è uguale al rango della matrice A’ ma questi due sono inferiori al numero di incognite del sistema (3). Pertanto dal teorema di Rouché-Frobenius sappiamo che si tratta di un sistema compatibile indeterminato (ICS):

Esercizio 3

Determina quale tipo di sistema è il seguente sistema di equazioni utilizzando il teorema di Rouché-Frobenius:

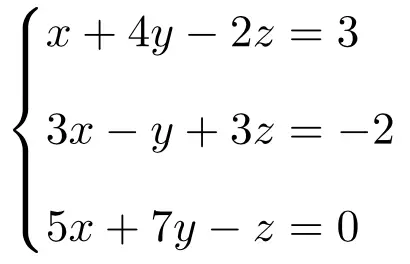
esercizio risolto passo passo del teorema di rouche - frobenius

vedi soluzione

Per prima cosa realizziamo la matrice A e la matrice estesa A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 4 & -2 & 3 \\[1.1ex] 3 & -1 & 3 & -2 \\[1.1ex] 5 & 7 & -1 & 0 \end{array} \right)$

Ora calcoliamo l’intervallo della matrice A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 1 & 4 \\[1.1ex] 3 & -1 \end{vmatrix} = -13 \neq 0$

Quindi la matrice A ha rango 2:

$\displaystyle rg(A)=2$

Una volta conosciuto il rango di A, calcoliamo il rango di A’. Sappiamo già che il determinante delle prime 3 colonne dà 0, ma non il determinante delle ultime 3 colonne:

$\displaystyle \begin{vmatrix} 4 & -2 & 3 \\[1.1ex]-1 & 3 & -2 \\[1.1ex] 7 & -1 & 0 \end{vmatrix} = -40 \neq 0$

Pertanto la matrice A’ ha rango 3 :

$\displaystyle rg(A')=3$

Il rango della matrice A è minore del rango della matrice A’, possiamo quindi dedurre dal teorema di Rouché-Frobenius che si tratta di un Sistema Incompatibile (SI) :

Esercizio 4

Determina il tipo del seguente sistema di equazioni a 3 incognite utilizzando il teorema di Rouché-Frobenius:

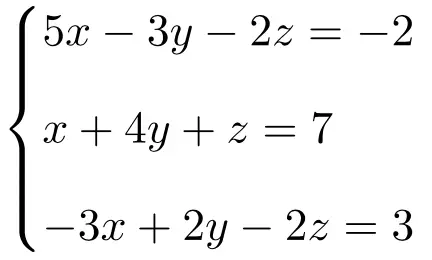
Rouche - Teorema di Frobenius esercizio risolto con 3 incognite e 3 equazioni

vedi soluzione

Per prima cosa realizziamo la matrice A e la matrice estesa A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 5 & -3 & -2 & -2 \\[1.1ex] 1 & 4 & 1 & 7 \\[1.1ex]-3 & 2 & -2 & 3 \end{array} \right)$

Dobbiamo ora calcolare il rango della matrice A. Per fare ciò risolviamo il determinante della matrice con la regola di Sarrus:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{vmatrix} = -40+9-4-24-10-6=-75 \bm{\neq 0}$

La matrice avente un determinante del terzo ordine diverso da 0, la matrice A ha rango 3:

$\displaystyle rg(A)=3$

Pertanto, anche la matrice A’ è di rango 3 , poiché è sempre almeno di rango A e non può essere di rango 4 perché non possiamo risolvere alcun determinante 4×4.

$\displaystyle rg(A')=3$

Quindi, grazie all’applicazione del teorema di Rouché-Frobenius, sappiamo che il sistema è un Sistema Determinato Compatibile (SCD), perché l’intervallo di A è uguale all’intervallo di A’ e al numero di incognite.

Esercizio 5

Identifica quale tipo di sistema utilizza il seguente sistema di equazioni utilizzando il teorema di Rouché-Frobenius:

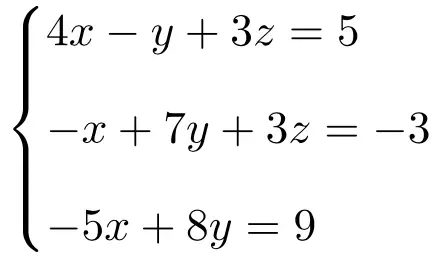
esempio del teorema di Rouche - frobenius

vedi soluzione

Per prima cosa realizziamo la matrice A e la matrice estesa A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 3 & 5 \\[1.1ex] -1 & 7 & 3 & -3 \\[1.1ex] -5 & 8 & 0 & 9 \end{array} \right)$

Ora calcoliamo l’intervallo della matrice A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 4 & -1 \\[1.1ex] -1 & 7 \end{vmatrix} = 27 \neq 0$

La matrice A è quindi di rango 2:

$\displaystyle rg(A)=2$

Una volta conosciuto il rango di A, calcoliamo il rango di A’. Il determinante delle prime 3 colonne che già conosciamo dà 0, ma il determinante delle ultime 3 colonne non dà:

$\displaystyle \begin{vmatrix} -1 & 3 & 5 \\[1.1ex] 7 & 3 & -3 \\[1.1ex] 8 & 0 & 9\end{vmatrix} = -408 \neq 0$

Pertanto la matrice A’ ha rango 3 :

$\displaystyle rg(A')=3$

E, infine, applichiamo il dominio al teorema di Rouché-Frobenius: il dominio della matrice A è più piccolo del dominio della matrice A’, è quindi un Sistema Incompatibile (SI) :

Esercizio 6

Classificare il seguente sistema di equazioni di ordine 3 con il teorema di Rouché-Frobenius:

$\begin{cases} 6x-2y+4z=1 \\[1.5ex] -2x+4y+3z= 7 \\[1.5ex] 8x-6y+z = -6\end{cases}$

vedi soluzione

Costruiamo innanzitutto la matrice A e la matrice estesa A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 6 & -2 & 4 & 1 \\[1.1ex] -2 & 4 & 3 & 7 \\[1.1ex] 8 & -6 & 1 & -6 \end{array} \right)$

Ora calcoliamo l’intervallo della matrice A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

Quindi la matrice A ha rango 2:

$\displaystyle rg(A)=2$

Una volta conosciuto il rango di A, calcoliamo il rango di A’. Sappiamo già che il determinante delle prime 3 colonne dà 0, quindi proviamo gli altri possibili determinanti 3×3:

$\displaystyle \begin{vmatrix} -2 & 4 & 1 \\[1.1ex]4 & 3 & 7 \\[1.1ex] -6 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix}6 & 4 & 1 \\[1.1ex] -2 & 3 & 7 \\[1.1ex] 8 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix} 6 & -2 & 1 \\[1.1ex] -2 & 4 & 7 \\[1.1ex] 8 & -6 & -6\end{vmatrix} = 0$

Tutti i determinanti 3×3 della matrice A’ sono 0, quindi neanche la matrice A’ sarà di rango 3. Tuttavia al suo interno sono presenti determinanti di ordine 2 diversi da 0. Ad esempio:

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

Quindi la matrice A’ sarà di rango 2 :

$\displaystyle rg(A')=2$

Infine, applicando il teorema di Rouché-Frobenius, sappiamo che si tratta di un Sistema Compatibile Indeterminato (ICS), perché l’intervallo della matrice A è uguale all’intervallo della matrice A’ ma questi due sono inferiori al numero di incognite presenti nella matrice sistema(3):

Teorema di rouche-frébenius

Cos’è il teorema di Rouché-Frobenius?

Enunciato del teorema di Rouché-Frobenius

Esempio di sistema compatibile determinato (SCD)

Esempio di sistema compatibile indeterminato (ICS)

Esempio di sistema incompatibile (IS)

Problemi risolti del teorema di Rouché-Frobenius

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Esercizio 6

Lascia un commento Annulla risposta