▷ Tasso di variazione medio e istantaneo (esercizi risolti)

Qui spieghiamo cosa sono il tasso di variazione, il tasso di variazione medio e il tasso di variazione istantaneo. Potrai vedere diversi esempi su come calcolare il tasso di variazione e, inoltre, potrai esercitarti con esercizi passo passo risolti sul tasso di variazione.

Qual è il tasso di cambiamento?

In matematica, il tasso di variazione (TV) di una funzione è la differenza tra i valori di una funzione in due punti diversi. Pertanto, per calcolare la velocità di variazione tra due punti, è necessario sottrarre i valori della funzione in questi due punti.

$\text{TV}[a,b]=f(b)-f(a)$

Ad esempio, se due immagini di una funzione sono f(2)=1 e f(5)=7, la loro velocità di variazione è:

$\text{TV}[2,5]=f(5)-f(2)=7-1=6$

Abbiamo appena visto il significato matematico di tasso di variazione, ma in economia il concetto di tasso di variazione significa quanto segue:

In economia, il tasso di variazione tra due valori è la differenza tra loro espressa in percentuale, ovvero il tasso di variazione di una variabile tra periodi diversi è la sua variazione relativa. Pertanto, per calcolare il tasso di variazione, si sottraggono i valori dei due diversi periodi e si divide il risultato ottenuto per il valore del periodo iniziale.

$\text{TV}[t,t+n]=\cfrac{Y_{t+n}-Y_t}{Y_t}\cdot 100$

Ad esempio, se il valore di alcune azioni aumenta da 35 € a 50 € in un mese, il suo tasso di variazione sarà:

$\text{TV}[t,t+1]=\cfrac{50-35}{35}\cdot 100=42,86 \ \%$

Considerando i due possibili significati di tasso di variazione, in questo articolo ci concentreremo sulla comprensione della definizione matematica di tasso di variazione. Si possono distinguere due tipi di tasso di variazione: il tasso di variazione medio e il tasso di variazione istantaneo. Di seguito è riportata la spiegazione di ciascun tipo.

Tasso medio di variazione

Il tasso medio di variazione (TVM) di una funzione in un intervallo è il numero di unità di cui la funzione aumenta (o diminuisce) per ciascuna unità di aumento della sua variabile indipendente. Pertanto, il tasso medio di variazione di una funzione viene calcolato dividendo la crescita della funzione in un intervallo per l’ampiezza dello stesso intervallo.

$\text{TVM}[a,b]=\cfrac{f(b)-f(a)}{b-a}$

Affinché tu possa vedere come viene calcolato il tasso di variazione medio, abbiamo risolto un esempio passo dopo passo di seguito.

Esempio di calcolo del tasso medio di variazione di una funzione

Calcolare il tasso medio di variazione nell’intervallo [2.5] della seguente funzione:

$f(x) = x^2-1$

Innanzitutto, calcoliamo il valore della funzione in x=2 e x=5:

$f(5)= 5^2-1=25-1=24$

$f(2)=2^2-1=4-1=3$

E poi calcoliamo il tasso medio di variazione della funzione nell’intervallo semplicemente applicando la formula:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,5]=\cfrac{f(5)-f(2)}{5-2} = \cfrac{24 - 3}{5-2} = \cfrac{21}{3} = \bm{7}$

Poiché il risultato di TVM[2,5] è positivo, ciò significa che la funzione cresce nell’intervallo [2,5]. Se invece il risultato fosse stato negativo, ciò significherebbe che la funzione diminuisce in questo intervallo.

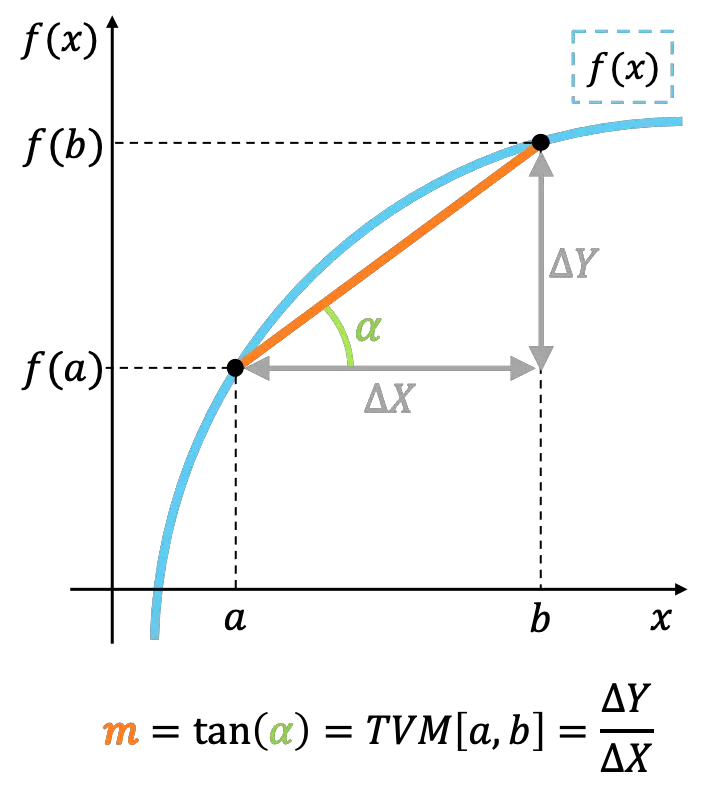
Interpretazione geometrica del tasso medio di variazione

Dal punto di vista geometrico, il tasso medio di variazione di una funzione in un intervallo rappresenta la pendenza della linea che congiunge i punti estremi dell’intervallo.

Tasso di cambiamento istantaneo

Il tasso di variazione istantaneo (TVI) di una funzione in un punto è il limite infinitesimo dell’aumento relativo della funzione in un intervallo. Pertanto, il tasso di variazione istantaneo viene calcolato risolvendo il limite del quoziente di f(a+h)-f(a) per cui h si avvicina a zero.

$\displaystyle\text{TVI}(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}$

Il valore del tasso di variazione istantaneo può essere positivo, negativo o zero e significa che la funzione in quel punto aumenta, diminuisce o rimane la stessa rispettivamente in quel punto.

Esempio di calcolo del tasso di variazione istantaneo di una funzione

Calcolare il tasso di variazione istantaneo nel punto x=2 della seguente funzione:

$f(x) = x^2$

Per calcolare il tasso di variazione istantaneo, dobbiamo applicare la formula:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h} = \lim\limits_{h \to 0} \cfrac{(2+h)^2-2^2}{h}$

Risolviamo l’identità notevole:

$\lim\limits_{h \to 0} \cfrac{2^2+h^2+2\cdot 2 \cdot h -2^2}{h} = \lim\limits_{h \to 0} \cfrac{4+h^2+4h -4}{h} = \lim\limits_{h \to 0} \cfrac{h^2+4h}{h}$

➤ Se non ricordi più le formule delle identità notevoli , troverai tutte le formule sul nostro sito specializzato in polinomi: www.polinomios.org

Ora proviamo a risolvere il limite:

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h} = \cfrac{0^2+4\cdot 0}{0} =\cfrac{0}{0}$

Ma troviamo zero indeterminazione tra zero, quindi:

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h}= \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+4)}{\cancel{h}} = \lim\limits_{h \to 0} (h+4)$

➤ Vedi: come risolvere un limite con indeterminazione pari a zero tra zero

E infine risolviamo il limite:

$\lim\limits_{h \to 0} (h+4) = 0 +4 = \bm{4}$

Ancora:

$\mathbf{TVI} \bm{(2) = 4}$

Poiché il risultato di TVI(2) è positivo, ciò significa che la funzione aumenta in x=2. D’altra parte, se il risultato fosse stato negativo, ciò significherebbe che in questa fase la funzione sta diminuendo.

Interpretazione geometrica della velocità di variazione istantanea

Dal punto di vista geometrico, la velocità di variazione istantanea di una funzione in un punto rappresenta la pendenza della linea tangente alla funzione in quello stesso punto.

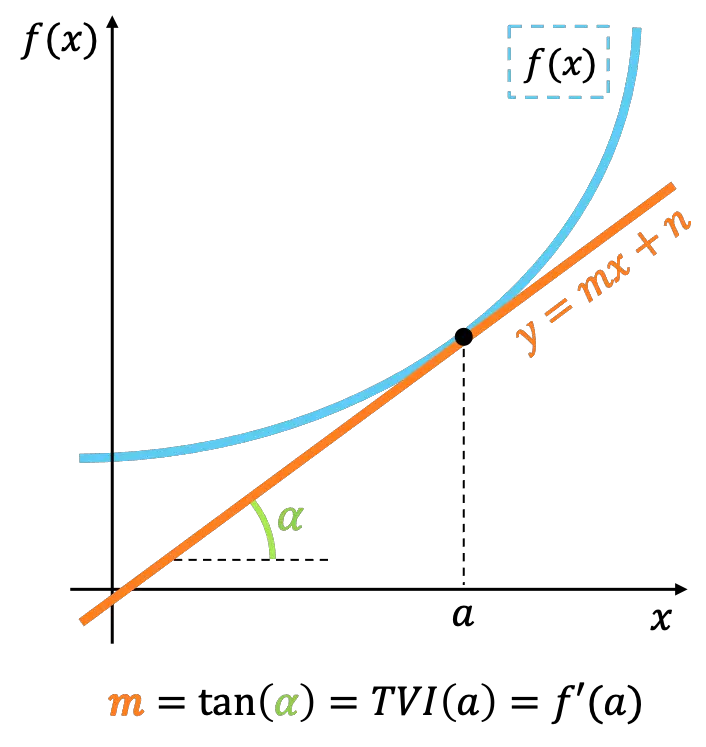
Se guardi da vicino, il significato di tasso di variazione istantaneo è equivalente al concetto di derivata di una funzione . Pertanto, il tasso di variazione istantaneo viene utilizzato anche per calcolare il valore della derivata di una funzione in un punto.

Esercizi risolti sul tasso di variazione

Esercizio 1

Calcolare il valore del tasso di variazione della seguente funzione nell’intervallo [1,3].

$f(x)=x^2-5$

Vedi la soluzione

Innanzitutto, determiniamo il valore della funzione alle estremità dell’intervallo:

$f(1)=1^2-5=1-5=-4$

$f(3)=3^2-5=9-5=4$

E ora applichiamo la formula del tasso di variazione:

$\text{TV}[a,b]=f(b)-f(a)$

$\text{TV}[1,3]=f(3)-f(1)=4-(-4)=4+4=\bm{8}$

Esercizio 2

Calcolare il tasso medio di variazione (TVM) della seguente funzione nell’intervallo [1,4]:

$f(x)=2x+1$

Vedi la soluzione

Per prima cosa calcoliamo le immagini della funzione in x=1 e x=4.

$f(4)=2\cdot4+1=9$

$f(1)=2\cdot 1+1=3$

E applichiamo la formula per il tasso di variazione medio:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [1,4] = \cfrac{f(4)-f(1)}{4-1} = \cfrac{9-3}{4-1}=\cfrac{6}{3} = \bm{2}$

Esercizio 3

Trova il tasso medio di variazione della seguente funzione nell’intervallo [-1.3]:

$f(x)=(x+1)^2$

Vedi la soluzione

Per determinare il tasso di variazione medio, dobbiamo prima calcolare f(-1) ef(3):

$f(3)=(3+1)^2=(4)^2=16$

$f(-1)=((-1)+1)^2=(0)^2=0$

Usiamo ora la formula per il tasso di variazione medio:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [-1,3] = \cfrac{f(3)-f(-1)}{3-(-1)} = \cfrac{16-0}{3+1}=\cfrac{16}{4} = \bm{4}$

Esercizio 4

Calcolare il tasso medio di variazione nell’intervallo [2,4] della funzione mostrata nel grafico seguente:

Vedi la soluzione

Applichiamo la formula per il tasso di variazione medio:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,4]=\cfrac{f(4)-f(2)}{4-2}$

Come vediamo nella formula, dobbiamo trovare il valore di f(4) ef(2). E questo può essere fatto facilmente guardando la rappresentazione grafica della funzione:

$f(4)=5$

$f(2)=1$

E ora che conosciamo i valori della funzione, li sostituiamo nella formula:

$\text{TVM}[2,4]=\cfrac{f(4)-f(2)}{4-2}=\cfrac{5-1}{4-2}=\cfrac{4}{2}=\bm{2}$

Esercizio 5

Calcolare il tasso di variazione istantaneo della seguente funzione nel punto x=2:

$f(x)=3x$

Vedi la soluzione

Per determinare la velocità istantanea di variazione della funzione nel punto x=2 applichiamo la formula corrispondente:

$\text{TVI}(a)=\lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\begin{array}{l}\text{TVI}(2)=\lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{3(2+h)-3\cdot 2}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{6+3h-6}{h}= \lim\limits_{h \to 0} \cfrac{3h}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{3\cancel{h}}{\cancel{h}}=\lim\limits_{h \to 0} 3 = \bm{3}\end{array}$

Esercizio 6

Determinare il tasso di variazione istantaneo (TVI) della seguente funzione nel punto x=1:

$f(x)=x^2+1$

Vedi la soluzione

Applichiamo la formula per il tasso di variazione istantaneo:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}$

Quindi, calcoliamo

$f(1+h)$

$f(1):$

$f(1+h) = (1+h)^2+1$

$f(1)=1^2+1=1+1=2$

E sostituiamo i valori trovati nel limite:

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}= \lim\limits_{h \to 0} \cfrac{(1+h)^2+1-2}{h} =\lim\limits_{h \to 0} \cfrac{(1+h)^2-1}{h}$

Risolviamo il prodotto notevole:

$\lim\limits_{h \to 0} \cfrac{1^2+h^2+2\cdot 1 \cdot h-1}{h}=\lim\limits_{h \to 0} \cfrac{1+h^2+2h-1}{h}=\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}$

Ora proviamo a risolvere il limite:

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\cfrac{0^2+2\cdot 0}{0} = \cfrac{0}{0}$

Ma troviamo la forma indeterminata zero divisa per zero, quindi fattorizziamo il polinomio del numeratore della frazione e semplifichiamo:

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\lim\limits_{h \to 0} \cfrac{h(h+2)}{h} = \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+2)}{\cancel{h}}= \lim\limits_{h \to 0}(h+2)$

➤ Se non sai come risolvere l’indeterminazione zero tra zero , puoi vedere la spiegazione completa nel link sopra su come risolvere un limite con indeterminazione zero tra zero.

E infine, risolviamo il limite:

$\lim\limits_{h \to 0}(h+2) = 0+2 =\bm{2}$

In sintesi, il tasso di variazione istantaneo della funzione nel punto x=1 è pari a 2.

$\mathbf{TVI} \bm{(1) = 2}$

Esercizio 7

Trovare il tasso di variazione istantaneo della seguente funzione nel punto x=2:

$f(x)=4x^2-x+3$

Vedi la soluzione

Utilizziamo innanzitutto la formula del tasso di variazione istantaneo:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}$

Calcoliamo

$f(2+h)$

$f(2):$

$f(2+h) = 4(2+h)^2-(2+h)+3=4(2+h)^2-h+1$

$f(2) =4\cdot 2^2-2+3=4\cdot 4-2+3 =17$

E sostituiamo i valori trovati nel limite:

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{4(2+h)^2-h+1-17}{h}=\\[4ex]= \lim\limits_{h \to 0} \cfrac{4(2+h)^2-h-16}{h}$

Calcoliamo l’uguaglianza notevole:

$\lim\limits_{h \to 0} \cfrac{4(2^2+h^2+2\cdot 2 \cdot h)-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4(4+h^2+4h)-h-16}{h}$

Operiamo sul numeratore:

$\lim\limits_{h \to 0} \cfrac{16+4h^2+16h-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}$

Ora proviamo a risolvere il limite:

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\cfrac{4\cdot0^2+15\cdot 0}{0} = \cfrac{0}{0}$

Ma otteniamo l’indeterminazione zero divisa per zero, quindi fattorizziamo i polinomi e semplifichiamo:

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\lim\limits_{h \to 0} \cfrac{h(4h+15)}{h}=\lim\limits_{h \to 0} \cfrac{\cancel{h}(4h+15)}{\cancel{h}}= \lim\limits_{h \to 0}(4h+15)$

E infine, risolviamo il limite:

$\lim\limits_{h \to 0}(4h+15)=4\cdot 0+15 =\bm{15}$

Ancora:

$\mathbf{TVI} \bm{(2) = 15}$

Qual è il tasso di cambiamento?

Tasso medio di variazione

Esempio di calcolo del tasso medio di variazione di una funzione

Interpretazione geometrica del tasso medio di variazione

Tasso di cambiamento istantaneo

Esempio di calcolo del tasso di variazione istantaneo di una funzione

Interpretazione geometrica della velocità di variazione istantanea

Esercizi risolti sul tasso di variazione

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Esercizio 6

Esercizio 7

Lascia un commento Annulla risposta