Triangolo di Tartaglia (o Pascal)

In questa pagina spieghiamo cos’è il triangolo di Tartaglia, detto anche triangolo di Pascal. Impariamo come costruire matematicamente il triangolo di Tartaglia (o Pascal), a cosa serve e quali sono tutte le sue proprietà. Infine, mostriamo come e quando è nato questo importantissimo triangolo.

Cos’è il triangolo di Tartaglia (o di Pascal)?

Il triangolo di Tartaglia , chiamato anche triangolo di Pascal , è una rappresentazione matematica di numeri interi ordinati sotto forma di triangolo. Il triangolo di Tartaglia (o Pascal) viene utilizzato per effettuare calcoli matematici.

Questa è la definizione del triangolo di Tartaglia o Pascal, ma sicuramente capirai meglio il concetto con un’immagine del triangolo:

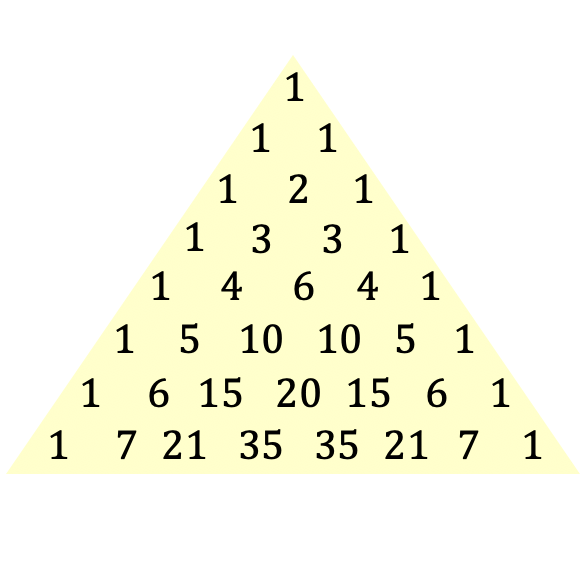
Il triangolo di Tartaglia è chiamato anche triangolo di Pascal dal nome del filosofo e matematico francese Blaise Pascal, che introdusse questa espressione triangolare nel 1654, sebbene questo triangolo fosse già conosciuto fin dall’antichità. Di seguito, approfondiremo la storia di questo particolare triangolo.

Come è costruito il triangolo di Tartaglia o di Pascal?

Come hai visto nel triangolo di Pascal (o Tartaglia), i numeri sono tanti, ma questo non significa che dobbiamo conoscerli a memoria (meno male). Esiste una formula che permette di trovare facilmente tutti i numeri del triangolo di Pascal o di Tartaglia, basta risolvere semplici somme.

Per costruire il triangolo di Tartaglia o Pascal, si inizia dalla parte superiore del triangolo, che è sempre un 1, e poi si calcolano le linee sottostanti. Ogni numero nelle righe seguenti è la somma dei due numeri direttamente sopra di esso, tranne le estremità delle righe che sono sempre 1.

Puoi quindi calcolare quante linee del triangolo di Tartaglia vuoi, perché puoi sommare successivamente le linee sommando i numeri.

A cosa serve il triangolo di Tartaglia o di Pascal?

Sapere come costruire il triangolo di Tartaglia è molto utile, ma… a cosa serve questo triangolo aritmetico? Ebbene, il triangolo di Tartaglia (o di Pascal) ha molte applicazioni in matematica, soprattutto nel campo dell’algebra.

numeri combinatori

Innanzitutto il triangolo di Tartaglia viene utilizzato per calcolare direttamente i numeri combinatori , detti anche coefficienti binomiali. Se non sai cosa sono questo tipo di operazioni, puoi cercarle sul nostro sito (abbiamo un motore di ricerca in alto a destra) perché abbiamo scritto un articolo dettagliato in cui spieghiamo come si risolvono e tu lì Tu troverai anche esempi ed esercizi risolti passo passo. Ma in sintesi, l’espressione algebrica di un numero combinatorio è la seguente:

$\displaystyle \begin{pmatrix} n \\ k \end{pmatrix}$

Ebbene, tutti i numeri combinatori possono essere facilmente determinati con il triangolo di Tartaglia, perché la soluzione di ciascun coefficiente binomiale equivale ad un numero di questa espressione triangolare come mostrato nella figura seguente:

numeri combinatori del triangolo di Tartaglia o Pascal

Ad esempio, il numero combinatorio

$\displaystyle \begin{pmatrix} 4 \\ 2 \end{pmatrix}$

restituisce 6, perché nel triangolo di Tartaglia invece c’è un 6.

Quindi, se sai costruire il triangolo di Tartaglia o di Pascal, puoi calcolare qualsiasi numero combinatorio velocemente e senza usare la loro formula.

Il binomio di Newton

Un altro utilizzo del triangolo di Tartaglia (o Pascal) è quello di poter calcolare le potenze dei binomi (clicca su questo link per scoprire cos’è un binomio).

Un esempio del potenziamento di un binomio sono identità notevoli, come:

$(a+b)^2$

Le identità notevoli sono molto importanti per la matematica, perché ci permettono di salvare molti calcoli e risolvere operazioni complicate in modo diretto e rapido. Ecco perché ti consigliamo di controllare il seguente link se ancora non saicosa sono le identità notevoli .

Come hai visto nel link precedente, i prodotti notevoli possono essere risolti direttamente con le loro formule. Ma… cosa succede quando la coppia viene elevata al cubo o ad un livello superiore?

$\begin{array}{c} (a+b)^3 = \ ? \\[3ex] (a+b)^4 = \ ? \\[3ex] (a+b)^5 = \ ? \\[3ex] \bm{\vdots} \end{array}$

Ebbene, questi binomi possono essere calcolati in modo molto semplice con il triangolo di Tartaglia grazie al teorema del binomio (o binomio di Newton). una volta padroneggiato il metodo è veloce da applicare, per spiegarlo bene serve una pagina intera. Quindi se sei più interessato a come risolvere questo tipo di binomi, clicca sulla pagina collegata e potrai vedere come si fa.

Combinatoria

Il triangolo di Tartaglia, o triangolo di Pascal, può essere utilizzato anche per determinare combinazioni e probabilità.

Se mai dovessimo incontrare un problema in cui dobbiamo determinare quanti gruppi diversi possono essere formati da un gruppo indipendentemente dall’ordine, possiamo utilizzare il triangolo di Tartaglia.

Ad esempio, se abbiamo 5 carte, per sapere in quanti modi possiamo sceglierne 3, basta andare sulla terza colonna (la prima colonna è zero) della quinta riga (la prima riga è anche riga 0) del triangolo di Tartaglia. Il numero in questa posizione (10) corrisponde al numero di possibilità che ci sono per scegliere 3 carte.

$1 \quad 5 \quad 10 \quad \color{blue}\boxed{ \color{black}10} \color{black} \quad 5 \quad 1$

Quindi da 5 carte si possono formare 10 diversi gruppi di tre carte.

Proprietà del triangolo di Tartaglia o Pascal

Il triangolo di Tartaglia, detto anche triangolo di Pascal, ha le seguenti caratteristiche:

Il triangolo di Tartaglia (o Pascal) è simmetrico, cioè la linea verticale che divide l’intero triangolo in due triangoli equilateri uguali è un asse di simmetria.

La somma orizzontale di tutti i numeri in qualsiasi linea del triangolo di Pascal è uguale a una potenza di 2.

proprietà del triangolo di Tartaglia o di Pascal

Importanti sono anche le diagonali del triangolo di Tartaglia: i numeri sulla prima diagonale (diagonale esterna) sono uno, la seconda diagonale è formata dalla successione di tutti i numeri naturali, la terza diagonale corrisponde ai numeri triangolari, e la quarta diagonale è composta di numeri tetragonali (o tetraedrici).

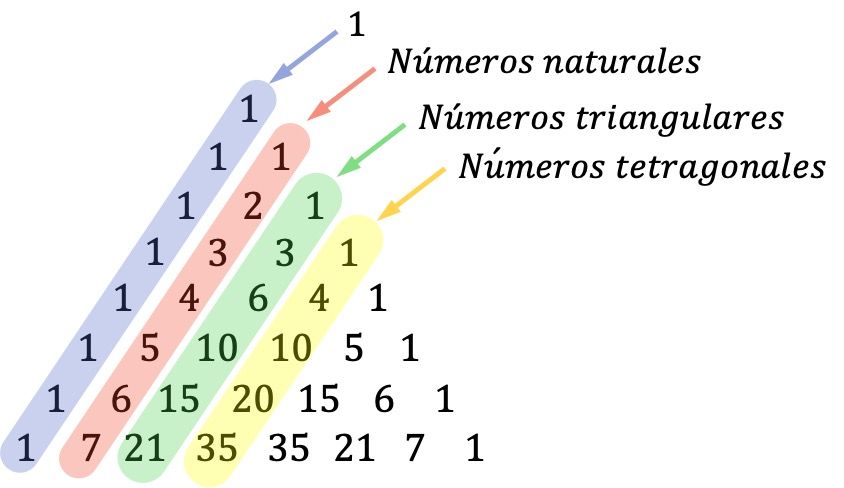
triangolo tartaglia o numeri triangolari e tetragonali pascal

I numeri triangolari sono numeri che possono essere rappresentati sotto forma di un triangolo. E i numeri tetragonali sono quelli che formano piramidi triangolari.

Se non sai cosa sono i numeri triangolari o tetragonali non succede nulla, è solo una curiosità sul triangolo di Tartaglia. Tuttavia, è necessario conoscere il significato dei numeri naturali (numeri utilizzati per contare gli elementi).

Ad eccezione del numero 1, se il primo numero di una riga è un numero primo, tutti i numeri della stessa riga sono divisibili per quel numero. Ad esempio, nell’ottava riga (1-7-21-35-35-21-7-1), i numeri 7, 21 e 35 possono essere divisi per 7 (sette è un numero primo).

Un’altra particolarità del triangolo di Tartaglia è che la serie di Fibonacci si può trovare sommando le diagonali in un certo modo:

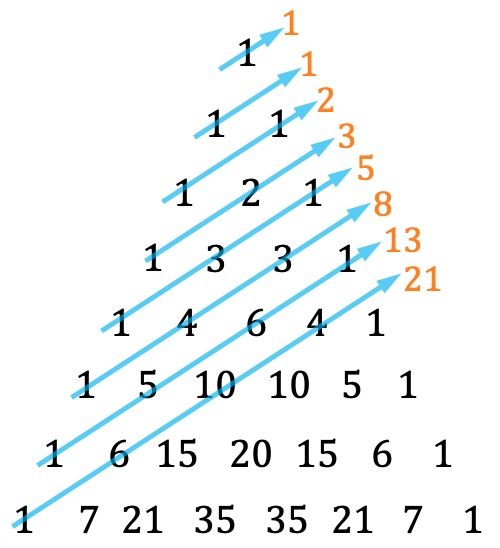
serie di fibonacci tartaglia o triangolo pascal

Ricorda che ogni termine della sequenza di Fibonacci è uguale alla somma dei due precedenti, i primi due termini sono 1 e 1. Pertanto i numeri che appartengono alla sequenza di Fibonacci sono: 1, 1, 2, 3, 5, 8 , 13, 21, 34, 55, 89, 144, 233,…

Se sommiamo due numeri consecutivi della terza diagonale del triangolo di Pascal (1-3-6-10-15-…) otteniamo un quadrato perfetto (1, 4, 9, 16, 25,…).

Se dipingiamo i numeri pari del triangolo di Pascal in un colore e i numeri dispari in un altro colore, otteniamo la figura del triangolo di Sierpinski, un famoso insieme geometrico. Qui sotto puoi vedere il triangolo di Pascal di altezza 512 rappresentato con i numeri dispari colorati di nero e i numeri pari colorati di bianco:

triangolo di tagliaglia o triangolo di pascal di sierpinski

La congettura di Singmaster dice che il numero di volte in cui si presenta ogni numero maggiore di 1 è finito. O in altre parole, sebbene il numero di righe nel triangolo di Tartaglia sia infinito, il numero di volte in cui appare ogni numero tranne 1 è finito. Per curiosità, il numero 3003 è l’unico finora noto ad apparire fino a otto volte nel triangolo.

Storia del triangolo di Tartaglia o Pascal

Ora che sappiamo come appare il triangolo di Tartaglia, vediamo quando è stato inventato questo triangolo matematico molto speciale.

Sebbene il nome del triangolo aritmetico sia attribuito principalmente ai famosi scienziati Tartaglia e Pascal, questo triangolo algebrico era già utilizzato prima.

La prima testimonianza di un triangolo formato da coefficienti binomiali risale al X secolo in India. Tuttavia, i persiani iniziarono a studiarne le proprietà, in particolare i matematici Al-Karaji (953-1029) e Omar Khayyam (1048-1131). Questo è il motivo per cui in Iran è stato reso popolare come il triangolo Khayyam-Pascal o anche semplicemente il triangolo Khayyam .

Questo triangolo cominciò ad essere introdotto in Cina nell’XI secolo dal matematico Jia Xian, ma fu più tardi nel XIII secolo che Yang Hui lo introdusse come triangolo aritmetico . E per questo motivo nel Paese asiatico lo chiamano triangolo Yang Hui .

Il triangolo matematico raggiunse più tardi il continente europeo attraverso il tedesco Petrus Apianus, appositamente pubblicato nell’anno 1527 nel suo libro Rechnung . Da lì, il famoso algebrista italiano Niccolò Fontana Tartaglia studiò approfonditamente il triangolo durante la prima metà del XVI secolo, e in suo onore in paesi come l’Italia è noto come triangolo di Tartaglia.

Infine, il francese Blaise Pascal dimostrò molte delle proprietà del triangolo studiate nella sua pubblicazione del Trattato sul triangolo aritmetico nel 1654, da cui il nome triangolo di Pascal. Va notato che alcune di queste proprietà erano già note, ma fu Pascal a realizzarne la dimostrazione per induzione matematica.

Triangolo di tartaglia (o di pascal).