Sottrazione vettoriale

In questa pagina vedrai come sottrarre due vettori, sia graficamente che numericamente. Per sottrarli graficamente esistono tre metodi: il parallelogramma, il triangolo e il poligono. Qui puoi distinguere i vantaggi e gli svantaggi di ciascun metodo. Inoltre troverai esempi, esercizi e problemi risolti passo dopo passo.

Come sottrarre graficamente due vettori?

Esistono diversi modi per sottrarre geometricamente i vettori. Ovviamente con tutti si ottiene lo stesso risultato, ma noi vi spiegheremo tutti i metodi affinché possiate scegliere quello che preferite. 👌

Per sottrarre solo 2 vettori esistono due procedimenti grafici: il metodo del parallelogramma e il metodo del triangolo . Se però vogliamo risolvere la sottrazione di 3 o più vettori dobbiamo utilizzare il metodo dei poligoni .

Quindi, e senza ulteriori indugi, di seguito trovi le spiegazioni di tutti questi metodi.

Metodo o regola del parallelogramma

La regola del parallelogramma o metodo del parallelogramma è un procedimento che permette di trovare la sottrazione di due vettori attraverso la sua rappresentazione grafica in modo molto semplice. I passaggi da seguire per applicare questo processo sono i seguenti:

1. Per prima cosa rappresentiamo i due vettori sul grafico e li posizioniamo nello stesso punto di applicazione, cioè poniamo le origini di entrambi i vettori nello stesso punto.
2. In secondo luogo, disegniamo il vettore opposto a quello che viene sottratto nell’operazione o, in altre parole, invertiamo il vettore che sottrae.
3. Quindi disegniamo una linea parallela al vettore cambiato di segno all’estremità del vettore che viene aggiunto. E ripetiamo il processo con l’altro vettore. Otterremo così il disegno di un parallelogramma (da qui il nome della regola).
4. Infine il risultato della sottrazione sarà il vettore che va dall’origine comune dei due vettori al punto in cui si intersecano le due rette parallele.

Considera il seguente esempio generico in cui due vettori vengono sottratti utilizzando il metodo del parallelogramma:

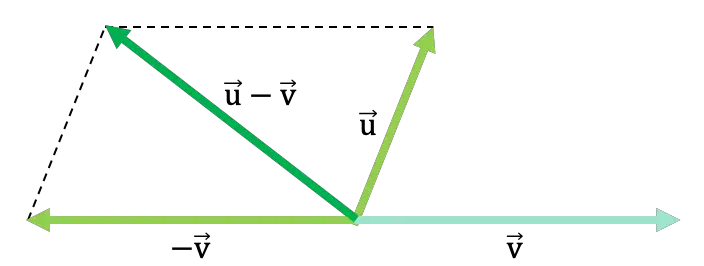
Metodo o regola del triangolo

Il metodo dei triangoli è un altro procedimento con cui si possono sottrarre due vettori dal loro grafico. In questo caso i passaggi da seguire sono:

1. Posizionare i due vettori nello stesso punto di applicazione, cioè in modo che i due vettori abbiano come origine lo stesso punto.
2. Il risultato della sottrazione vettoriale è il segmento che va dalla fine del vettore sottrattore alla fine dell’altro vettore. Se guardi da vicino, un triangolo viene completato con i due vettori sottratti e il vettore sottratto.

Ecco un esempio di sottrazione vettoriale utilizzando il metodo del triangolo:

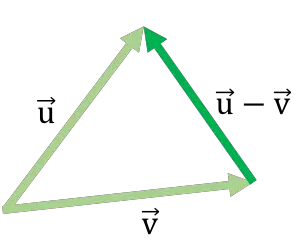
Questo modo di sottrarre i vettori è simile al metodo testa e coda utilizzato per aggiungere i vettori .

metodo del poligono

Una volta visto come risolvere graficamente la sottrazione di due vettori, vedremo come si fa quando abbiamo più di due vettori.

Quando vuoi sottrarre tre o più vettori, esiste una tecnica per andare più veloce nel calcolo e sottrarre tutti i vettori contemporaneamente. Questa tecnica è chiamata metodo del poligono e consiste nell’applicare successivamente il metodo di addizione di vettori testa-coda.

Ora probabilmente starai pensando: aggiungere vettori? È corretto erroneamente… Ebbene no! eh eh

Si scopre che sottrarre due vettori equivale ad aggiungere un vettore più il vettore opposto (o negativo) del vettore sottrattivo. Ciò è dovuto alle proprietà di addizione e sottrazione dei vettori:

Pertanto, i passaggi che dobbiamo seguire per sottrarre 3 o più vettori con il metodo dei poligoni sono:

1. Per prima cosa dobbiamo trovare il vettore inverso di ciascun vettore di sottrazione. È semplice come invertire la direzione e la direzione di tutti i vettori sottratti.
2. Quindi posizioniamo ciascun vettore opposto accanto al vettore che non sottrai, uno dopo l’altro. In modo che l’origine di un vettore coincida con la fine di un altro vettore.
3. Infine, il risultato della sottrazione vettoriale è il vettore ottenuto unendo l’inizio del primo vettore alla fine dell’ultimo vettore.

Guarda il seguente esempio in cui viene eseguita una sottrazione con 4 vettori:

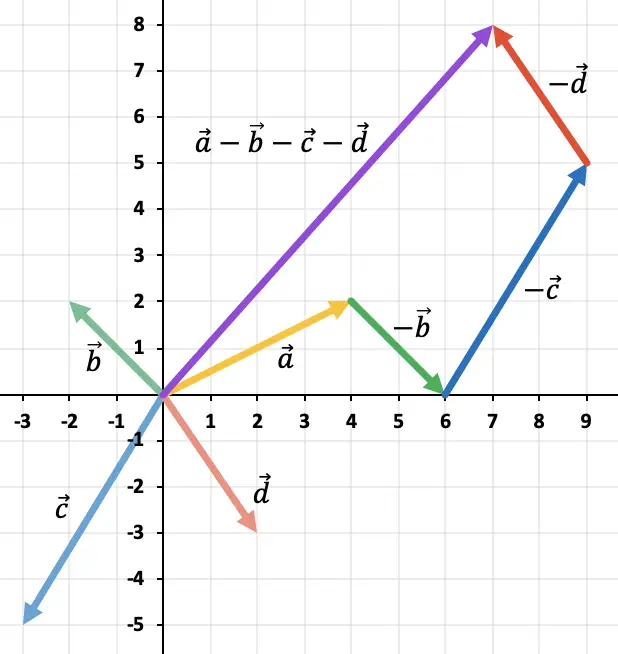
Si noti che per trovare il vettore opposto di un vettore è necessario che le due componenti di detto vettore cambino segno.

Come calcolare numericamente la sottrazione di due vettori?

Una volta che sappiamo già come sottrarre i vettori dal grafico, vedremo come calcolare numericamente o algebricamente una sottrazione vettoriale.

Ad esempio, la sottrazione tra vettori

E

Est:

Problemi di sottrazione vettoriale risolti

Esercizio 1

Calcola graficamente la sottrazione vettoriale

meno

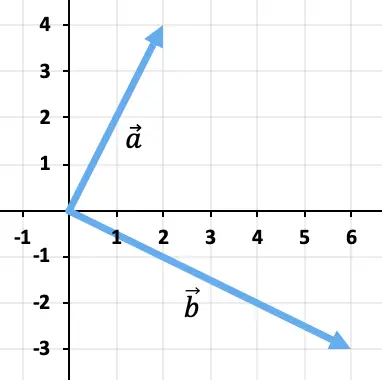
Per sottrarre i due vettori utilizzeremo il metodo del triangolo. I punti sono già posizionati nello stesso punto di applicazione (l’origine delle coordinate), quindi il risultato della sottrazione sarà il vettore che va dalla fine di

alla fine di

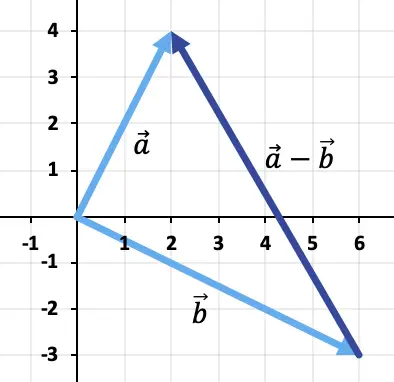
Esercizio 2

Trova graficamente la sottrazione di vettori

meno

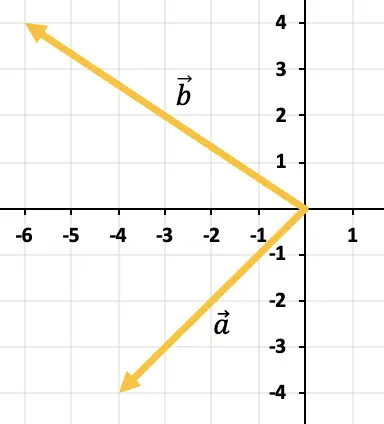
Per sottrarre i due vettori utilizzeremo la regola del triangolo. I punti sono già posizionati nello stesso punto di applicazione (all’inizio dell’asse X e dell’asse Y), quindi il risultato della sottrazione sarà il vettore che va dalla fine di

alla fine di

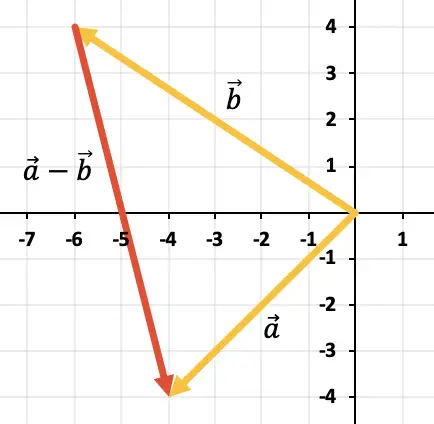
Esercizio 3

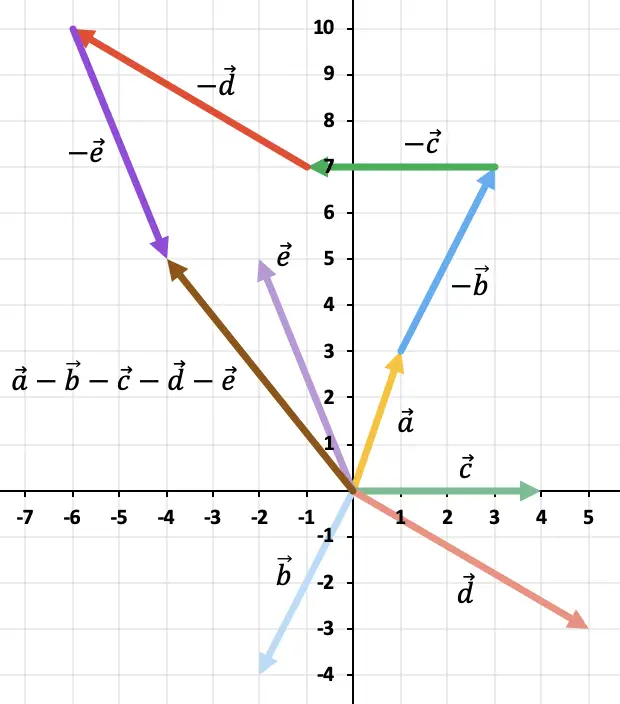
Risolvi graficamente la seguente operazione vettoriale:

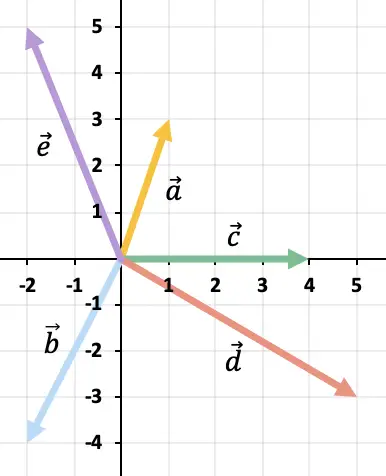
Poiché ci sono più di 2 vettori, utilizzeremo la regola del poligono per risolvere la sottrazione vettoriale. Per fare ciò, dobbiamo rappresentare uno dopo l’altro i vettori opposti dei restanti vettori. E il risultato sarà il vettore che parte dall’origine del vettore

fino al punto in cui termina l’ultimo vettore opposto.

Esercizio 4

Determina numericamente il risultato della sottrazione dei seguenti vettori:

Per sottrarre numericamente due vettori, è necessario sottrarre le rispettive coordinate:

Esercizio 5

Risolvi analiticamente la seguente operazione vettoriale:

Per sottrarre numericamente (o analiticamente) i vettori dobbiamo sottrarre le rispettive componenti: