Aggiunta di vettore

Questa pagina spiega come sommare due vettori nel piano, graficamente e numericamente. Esistono 3 modi per sommarli graficamente: il metodo del parallelogramma, testa-coda e poligono. Inoltre, troverai anche esercizi risolti sull’addizione di vettori e tutte le proprietà dell’addizione di vettori.

Come sommare graficamente due vettori?

Fondamentalmente ci sono due modi per aggiungere vettori dalla loro rappresentazione grafica. Con entrambe le forme si ottiene lo stesso risultato, ma alcuni preferiscono sommarle utilizzando il metodo testa-coda e altri con il metodo del parallelogramma . Ti spiegheremo quindi i due metodi affinché tu scelga quello che preferisci. 😉

D’altra parte questi due metodi vengono utilizzati per sommare due vettori, ma cosa succede se vogliamo sommare più di due vettori? È quindi necessario utilizzare il metodo del poligono , che consiste nell’utilizzare successivamente il metodo del parallelogramma. Troverai la sua spiegazione anche dopo i metodi testa-coda e parallelogramma.

Metodo o regola del parallelogramma

La regola del parallelogramma o metodo del parallelogramma (o legge del parallelogramma) è un procedimento grafico che permette di trovare la somma di due vettori in modo molto semplice. I passaggi da seguire per applicare questo processo sono i seguenti:

1. Per prima cosa disegniamo i vettori e li posizioniamo nello stesso punto di applicazione, cioè poniamo le origini di entrambi i vettori nello stesso punto.
2. Quindi disegniamo alla fine di un vettore una linea parallela all’altro vettore. E ripetiamo il passaggio con l’altro vettore. Otterremo quindi il disegno di un parallelogramma (da qui il nome della regola).
3. Infine il risultato della somma sarà il vettore che va dall’origine comune al punto in cui si intersecano le due rette parallele.

Guarda il seguente esempio generico in cui due vettori vengono sommati con la regola del parallelogramma:

Il risultato della somma dei vettori è la diagonale del parallelogramma che formano con i loro paralleli.

metodo della testa e della coda

Il metodo della testa e della coda , detto anche metodo del triangolo , è un altro procedimento con il quale è possibile sommare graficamente due vettori. In questo caso i passaggi da seguire sono:

1. Sposta un vettore aggiunto e posizionalo in modo che la sua origine sia proprio alla fine dell’altro vettore aggiunto.
2. Il risultato della somma dei vettori è il segmento che va dall’inizio del primo vettore aggiunto alla fine dell’altro vettore. Se guardi da vicino, un triangolo viene completato con la somma dei due vettori e il vettore sommato.

Ecco un esempio di addizione di vettori utilizzando il metodo testa-coda:

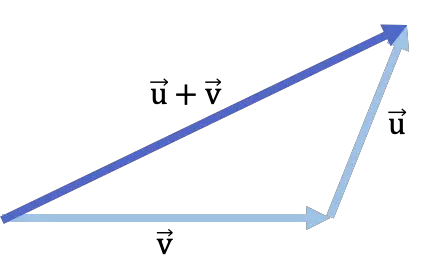
metodo del poligono

Una volta visto come risolvere graficamente la somma di due vettori, vedremo come si fa quando abbiamo più di due vettori.

Quando si vogliono sommare tre o più vettori, esiste una tecnica per velocizzare il calcolo dell’operazione. Questa tecnica è chiamata metodo del poligono e consiste nell’applicare successivamente il metodo testa-coda:

1. Dobbiamo prima posizionare ciascun vettore dopo l’altro, in modo che l’origine di un vettore coincida con la fine di un altro vettore. L’ordine in cui li posizioniamo è irrilevante.
2. E il risultato della somma è il vettore ottenuto unendo l’inizio del primo vettore alla fine dell’ultimo vettore.

Guarda il seguente esempio in cui vengono aggiunti 4 vettori:

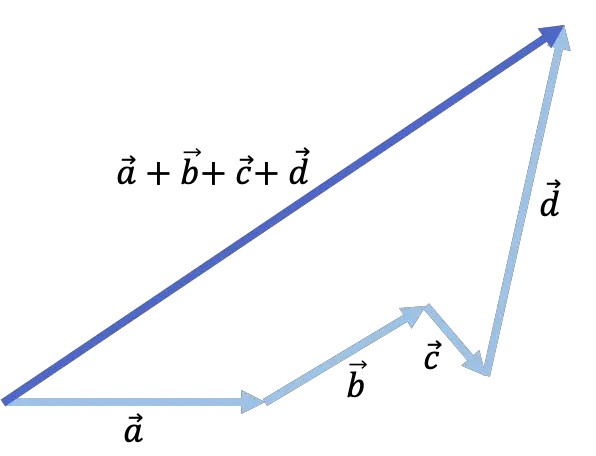
Calcolare numericamente la somma di due vettori

Una volta che sappiamo come sommare geometricamente i vettori, vedremo come calcolare numericamente o algebricamente la somma di un vettore.

Ad esempio, la somma tra vettori

E

Est:

D’altra parte bisogna tenere presente che la somma vettoriale di due vettori non è la stessa cosa della somma dei moduli dei vettori, infatti i risultati sono totalmente diversi. Puoi vedere le differenze tra le due operazioni nelle proprietà della grandezza del vettore (chiamata anche grandezza del vettore).

Aggiungi proprietà vettoriali

L’addizione vettoriale ha le seguenti caratteristiche:

• Proprietà associativa : Mettere tra parentesi la somma di più vettori non modifica il risultato dell’operazione.

• Proprietà commutativa – A differenza della sottrazione vettoriale, il risultato dell’addizione tra due vettori è indipendente dall’ordine in cui vengono sommati.

• Proprietà dell’elemento opposto : la somma di un vettore più il suo opposto, cioè la sua negazione, è uguale a 0.

• Proprietà dell’elemento neutro : ovviamente qualsiasi vettore più il vettore nullo o nullo è equivalente al vettore stesso:

Risolti problemi di addizione di vettori

Esercizio 1

Calcolare graficamente la somma dei vettori

E

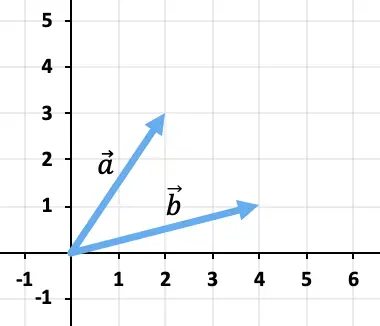
Per sommare i due vettori utilizzeremo la regola della testa e della coda. Posizioneremo quindi l’origine del vettore

alla fine del vettore

, e la somma sarà il vettore che va dall’origine delle coordinate alla fine di

Pertanto, il risultato dell’addizione vettoriale è:

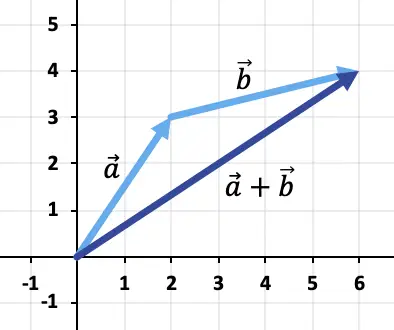
Esercizio 2

Risolvi graficamente la somma dei vettori

E

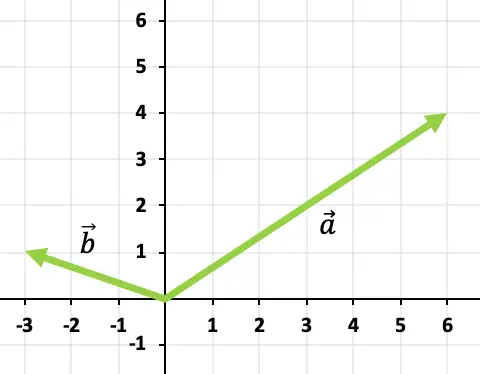
Per sommare i due vettori utilizzeremo la regola testa-coda. Localizzeremo quindi l’origine del vettore

alla fine del vettore

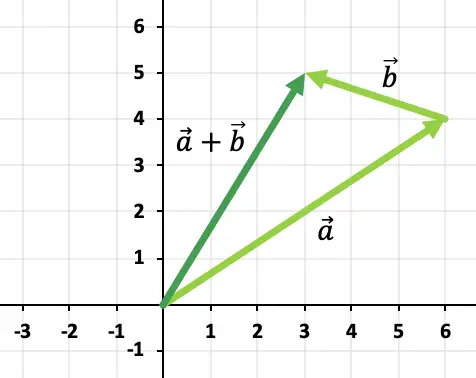
, e il vettore somma sarà quello che va dall’origine degli assi alla fine di

Pertanto, il risultato dell’addizione vettoriale è:

Esercizio 3

Determinare graficamente il vettore risultante dalla somma di tutti i vettori rappresentati nel grafico:

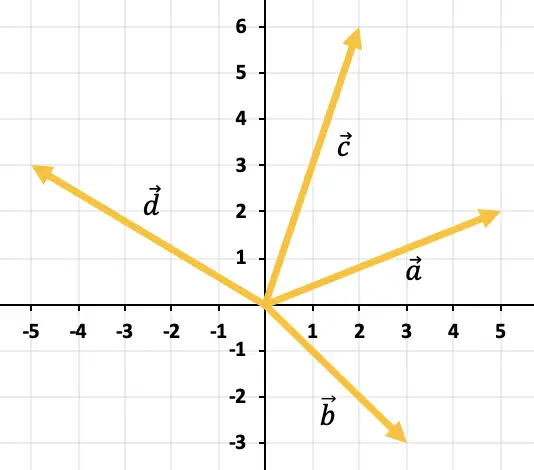
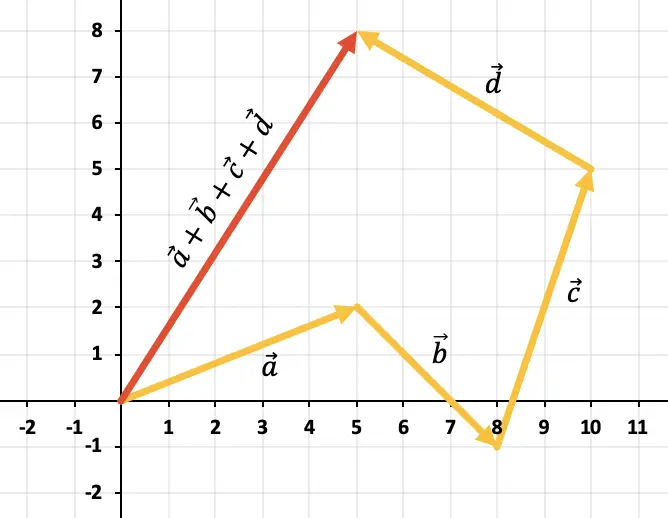
Per aggiungere più di 2 vettori dal grafico, è necessario utilizzare la regola del poligono. Dobbiamo quindi spostare i vettori in modo che rimangano continui, cioè uno dopo l’altro (l’ordine è irrilevante). Quindi la somma di tutti i vettori sarà il vettore che va dall’origine del primo vettore alla fine dell’ultimo vettore.

Quindi il risultato della somma dei 4 vettori è il vettore rappresentato in rosso:

Esercizio 4

Trova numericamente la somma dei seguenti vettori:

Per sommare numericamente due vettori, è necessario sommare le rispettive coordinate:

Esercizio 5

Calcolare analiticamente la somma dei seguenti vettori:

Per aggiungere numericamente i vettori, è necessario aggiungere le rispettive coordinate: