I sistemi di equazioni sono insiemi di due o più equazioni che hanno più di un’incognita. Quindi, per risolvere i sistemi, possiamo utilizzare quattro metodi: sostituzione, equalizzazione, riduzione e graficazione. Ma, prima di iniziare a spiegare le procedure risolutive, definiremo le tipologie di sistemi esistenti in base al numero di soluzioni:
- Sistema compatibile determinato: ha una sola soluzione e può essere rappresentato da due rette che si intersecano in un unico punto (che è la soluzione).
- Sistema compatibile indeterminato: ha infinite soluzioni e questo è dovuto al fatto che esistono due rette che coincidono negli stessi punti.
- Sistema incompatibile: non ha soluzione, poiché le rette sono parallele e quindi non hanno alcun punto in comune.
Metodi per la risoluzione di sistemi di equazioni lineari
Spiegheremo ora i diversi sistemi che possiamo utilizzare per risolvere sistemi di equazioni. Nelle spiegazioni troverai la teoria e alcuni esempi, grazie ai quali tutti i concetti spiegati saranno più chiari. Tieni presente che in questo articolo parleremo solo di sistemi di equazioni 2×2 , il che significa che ci occuperemo semplicemente di sistemi composti da due equazioni. Detto questo cominciamo con la spiegazione.
metodo di sostituzione
Il metodo di sostituzione consiste nell’isolare una delle incognite in una delle equazioni e quindi sostituire l’espressione ottenuta nell’equazione opposta. Questo metodo è maggiormente consigliato quando almeno una delle incognite ha il valore del coefficiente pari a 1. Pertanto, i passaggi da seguire sono molto semplici:
- Isolare una quantità sconosciuta da una delle due equazioni.
- Sostituiamo nell’altra equazione l’espressione equivalente all’incognita che abbiamo eliminato dalla prima equazione.
- Cancella l’incognita opposta nell’equazione che abbiamo ottenuto.
- Una volta ottenuto il valore della prima variabile, dobbiamo usarlo per trovare la seconda.
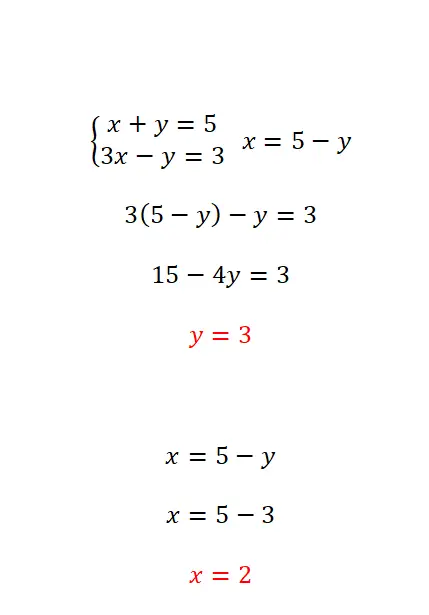
metodo di equalizzazione
Il metodo di abbinamento consiste nell’isolare la stessa variabile nelle due equazioni quindi abbinare le due espressioni ottenute. Questo metodo è consigliato quando è possibile isolare facilmente la stessa incognita in entrambe le equazioni, poiché semplifica l’intero calcolo. La procedura da seguire in questo caso è la seguente:
- Isoliamo l’incognita che abbiamo scelto nelle due equazioni.
- Assimiliamo le espressioni equivalenti a questo sconosciuto.
- Risolviamo l’equazione normalmente.
- Calcoliamo l’altra incognita con il valore che abbiamo calcolato.
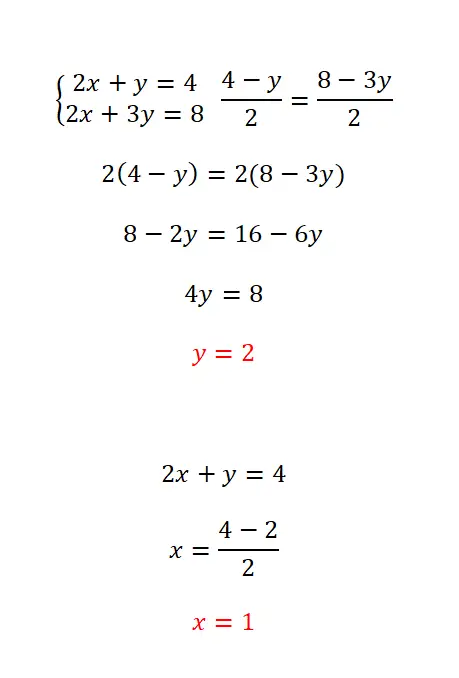
metodo di riduzione
Il metodo di riduzione si basa sulla moltiplicazione di entrambe le equazioni per due numeri, il che permette di ottenere lo stesso coefficiente con segno diverso di una delle variabili in entrambe le espressioni. Questo metodo è maggiormente consigliato quando la stessa incognita ha lo stesso coefficiente in tutte le equazioni o nel caso in cui si abbiano gli stessi coefficienti di segno opposto. E la procedura di risoluzione è la seguente:
- Si moltiplicano le due equazioni per i numeri necessari (bisogna trovare due numeri che permettano di ottenere lo stesso coefficiente per una delle due variabili nelle due equazioni, ma di segno opposto).
- Quindi le equazioni vengono sottratte o aggiunte per eliminare questa incognita con i rispettivi coefficienti.
- Quindi l’equazione rimanente viene risolta.
- E usiamo il risultato di questa equazione per ottenere il valore numerico che ci manca nell’altra variabile.
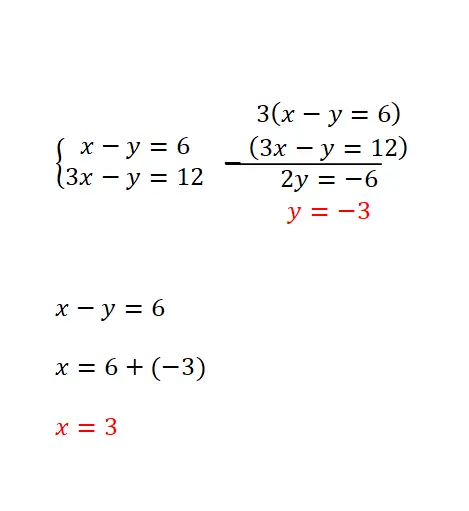
metodo grafico
Infine, possiamo scegliere di risolvere un sistema di equazioni mediante una rappresentazione grafica . Questo metodo è abbastanza diverso dagli altri, perché non ha una parte matematica complessa, è quasi interamente grafica. Quindi, per conoscere i valori delle incognite, dobbiamo strutturare le due equazioni nella forma dell’equazione della retta: y = mx + b . In questo modo potremo effettuare la rappresentazione poi, assoceremo i valori delle coordinate del punto di taglio tra le due funzioni alle incognite. Ecco un esempio pratico:
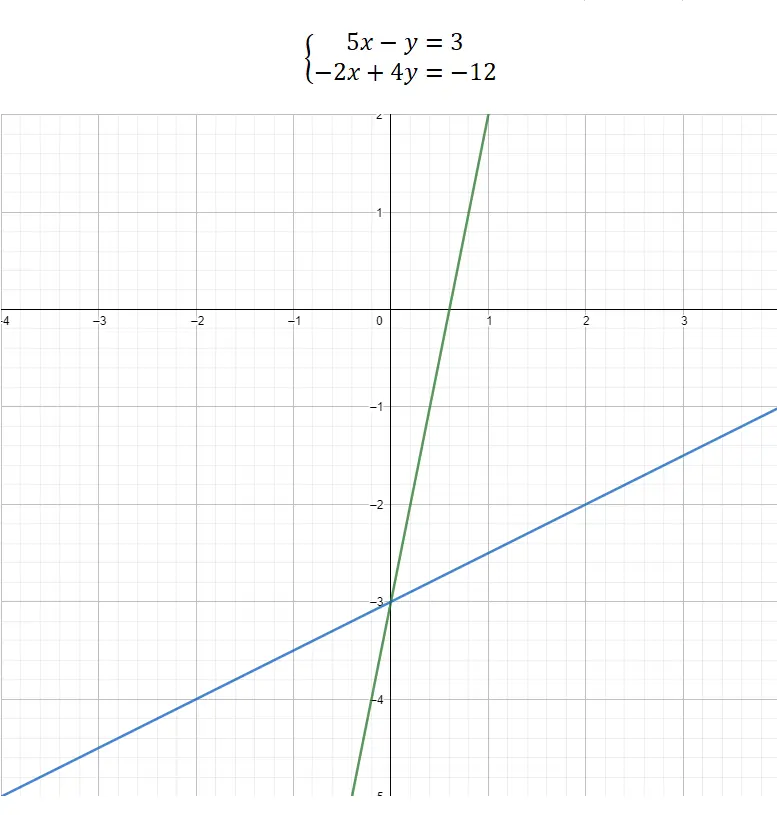
Come si può vedere nel grafico, il punto di interruzione tra le due funzioni è (0, -3). Pertanto, il valore di x = 0 e il valore di y = -3. Ecco come viene risolto graficamente un sistema di equazioni.
Come risolvere un sistema di equazioni quadratiche?
Per risolvere sistemi di equazioni quadratiche, possiamo usare i metodi che abbiamo appena discusso. Personalmente ci piace consigliare il metodo della sostituzione perché permette di ottenere velocemente un’equazione con una sola incognita. Se invece utilizziamo i metodi di riduzione o di equalizzazione il calcolo diventa piuttosto complicato. Quindi, una volta sostituita una delle due variabili, devi solo risolvere l’equazione quadratica risultante o l’equazione quadratica . Ecco un esempio in modo da poter vedere l’intero processo:
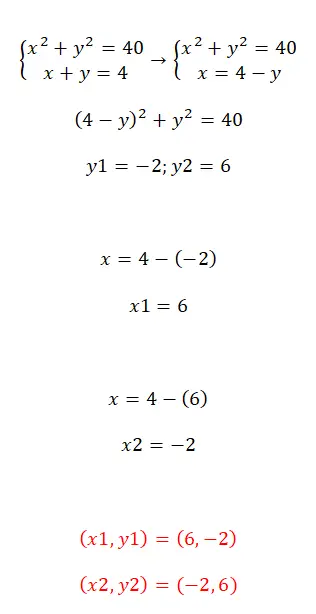
Esercizi sulla risoluzione di sistemi di equazioni
Ti proponiamo ora alcuni esercizi sui sistemi di equazioni lineari e quadratiche affinché tu possa applicare la teoria spiegata. In questo modo capirai meglio tutti i concetti relativi al calcolo dei sistemi di equazioni. Ti consigliamo di provare a risolverli prima di guardare le risposte che offriamo, in questo modo otterrai il massimo dagli esercizi:
Esercizio 1
Risolvi questo sistema di equazioni utilizzando il metodo di sostituzione:
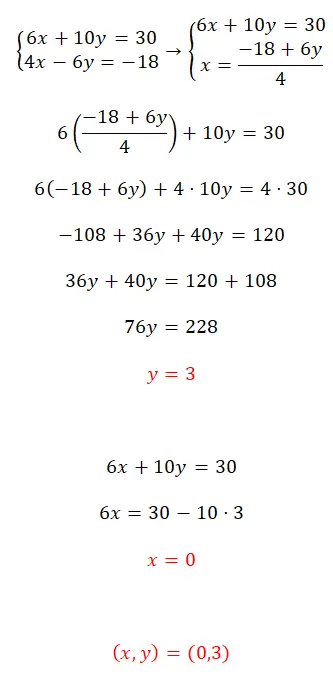
- Iniziamo isolando una delle due incognite in un’equazione.
- Sostituiamo poi l’espressione ottenuta nell’equazione opposta, con l’incognita che abbiamo risolto in precedenza.
- Otteniamo quindi il risultato della variabile opposta.
- Successivamente, sostituiamo il primo valore scoperto in una delle due equazioni per calcolare il valore della prima incognita.
- Infine esprimiamo il risultato delle due variabili.
Esercizio 2
Risolvi questo sistema di equazioni utilizzando il metodo di sostituzione:
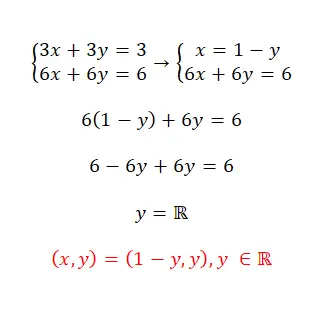
- In questo caso seguiremo la stessa procedura: isolare un’incognita, sostituirla nell’altra espressione e isolare la seconda variabile.
- Come possiamo vedere, questo è un sistema compatibile indeterminato, perché ha infinite soluzioni.
Esercizio 3
Risolvi questo sistema di equazioni utilizzando il metodo dell’equalizzazione:
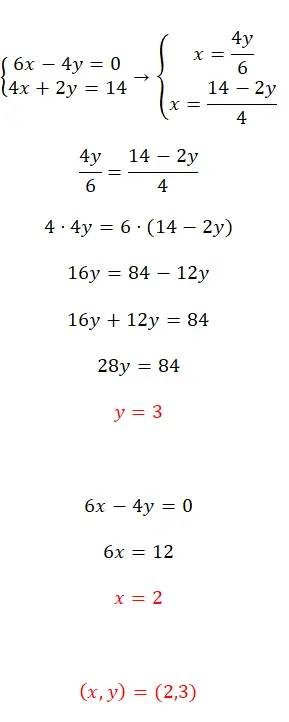
- Il primo passo è isolare la stessa variabile in entrambe le equazioni, in questo caso abbiamo scelto x.
- Quindi abbiniamo le espressioni risultanti e iniziamo a risolvere.
- Otteniamo così il valore della prima incognita.
- E se lo sostituiamo in una delle due equazioni originali, possiamo calcolare la seconda incognita.
- Infine esprimiamo il risultato delle due variabili.
Esercizio 4
Risolvi questo sistema di equazioni utilizzando il metodo dell’equalizzazione:
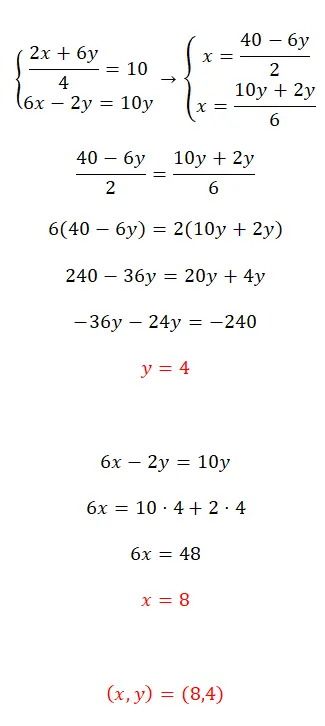
- Per prima cosa isoliamo la x in entrambe le equazioni.
- Successivamente, abbiniamo le espressioni che abbiamo ottenuto.
- Otteniamo il valore della prima incognita.
- Sostituiamo questo valore in una delle due equazioni iniziali e calcoliamo la seconda incognita.
- Infine esprimiamo il valore dei due sconosciuti.
Esercizio 5
Risolvi questo sistema di equazioni utilizzando il metodo di riduzione:
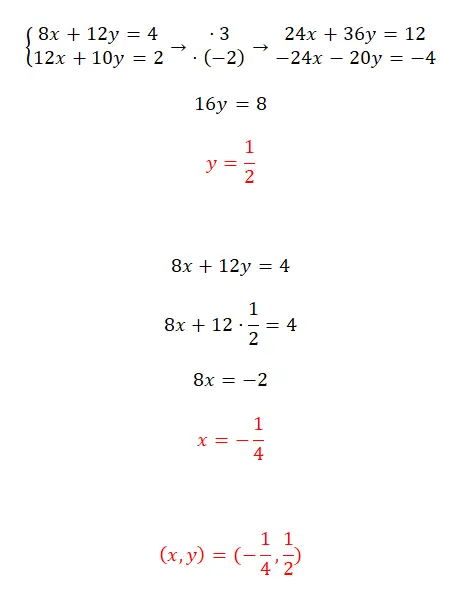
- Bisogna cercare due numeri che permettano di ottenere lo stesso coefficiente per una delle due variabili nelle due equazioni, ma di segno opposto .
- Quindi, risolvi semplicemente l’equazione che otteniamo sommando le due espressioni ottenute.
- Successivamente, sostituiamo la y in una delle due equazioni originali, per calcolare la x.
- Infine esprimiamo il risultato del sistema.
Esercizio 6
Risolvi questo sistema di equazioni utilizzando il metodo di riduzione:
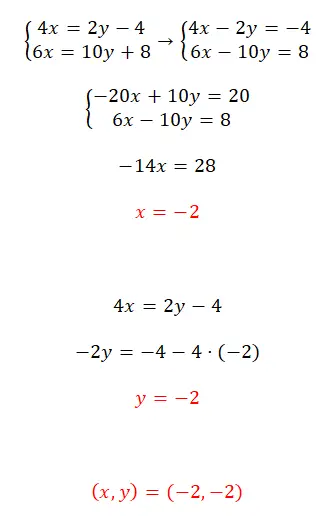
- Iniziamo sistemando le equazioni (passando tutte le variabili a sinistra).
- Quindi moltiplichiamo la prima equazione per -5.
- Risolviamo l’equazione che otteniamo sommando le due equazioni e otteniamo il valore di x.
- Usiamo questo valore noto per ottenere il valore di y.
- Esprimiamo il risultato del sistema di equazioni.
Esercizio 7
Risolvi questo sistema di equazioni utilizzando il metodo di sostituzione:
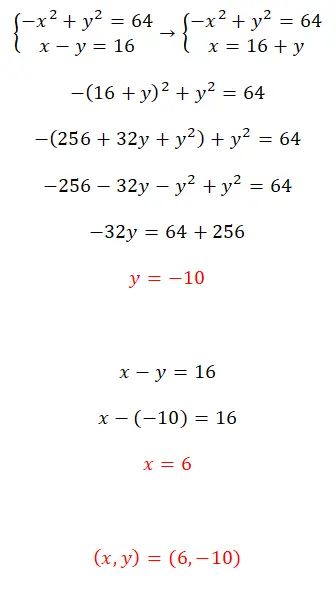
- Per risolvere questo sistema di equazioni non lineari, consigliamo di utilizzare il metodo di sostituzione.
- Quindi costruisci un’equazione con l’espressione equivalente a x.
- Ottieni il valore dell’incognita y.
- Calcola il valore di x con il valore calcolato in precedenza.
- E hai già entrambi i valori.
Esercizio 8
Risolvi questo sistema di equazioni utilizzando il metodo che preferisci:
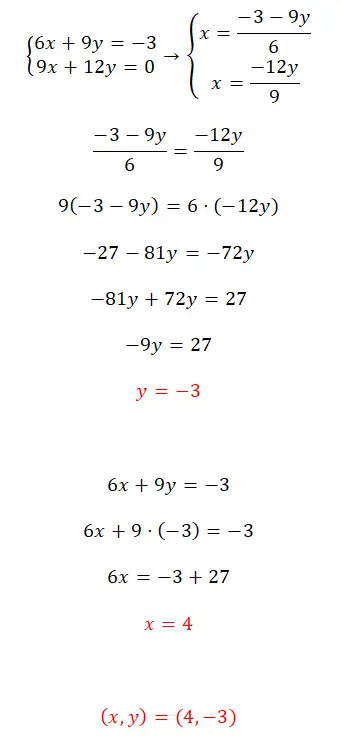
- In questo caso ci viene presentato un determinato sistema compatibile e lo risolveremo utilizzando il metodo dell’equalizzazione.
- Pertanto, risolviamo x in entrambe le equazioni e impostiamo uguali le due espressioni risultanti.
- Dopo aver risolto l’equazione, otteniamo il valore di y.
- Usiamo questo valore per trovare il valore di x.
- Infine esprimiamo il risultato del sistema.