In questo articolo spieghiamo cosa sono le funzioni simmetriche (funzioni pari e dispari) e come studiare la simmetria di una funzione. Potrai anche vedere le proprietà di questo tipo di funzioni e, infine, potrai esercitarti con esercizi risolti passo passo su funzioni simmetriche.
Cos’è una funzione simmetrica?
Una funzione simmetrica è una funzione in cui è possibile trovare un asse di simmetria nella sua rappresentazione grafica. Esistono due tipi di funzioni simmetriche: funzioni pari, simmetriche rispetto all’asse Y, e funzioni dispari, simmetriche rispetto all’origine delle coordinate.
Ricorda che un asse di simmetria è una linea immaginaria che divide qualsiasi cosa in due parti in modo che i loro punti opposti siano equidistanti l’uno dall’altro.
anche funzioni
Le funzioni pari sono funzioni simmetriche rispetto all’asse y, ovvero l’asse Y è un asse di simmetria della funzione.
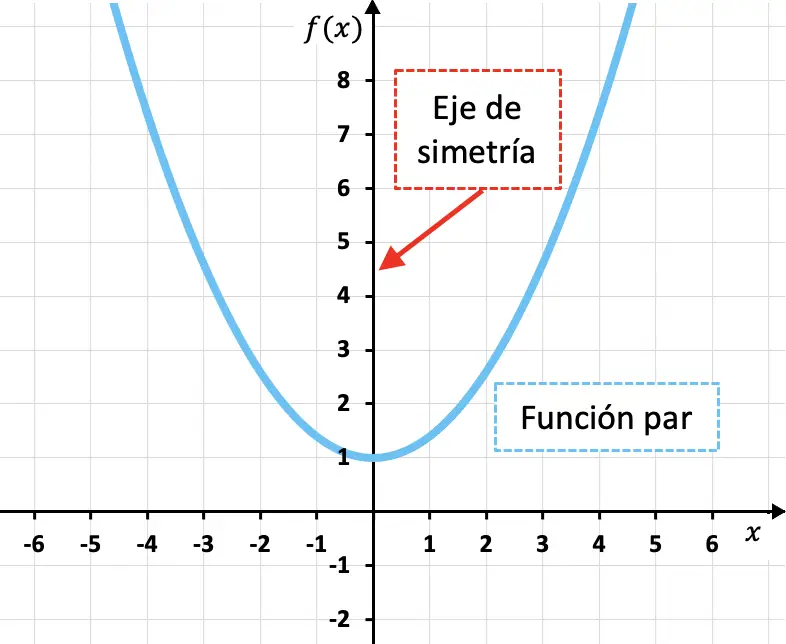
Come puoi vedere nella funzione quadratica mostrata sopra, l’immagine di una funzione pari per qualsiasi valore della variabile indipendente (x) è equivalente all’immagine della funzione per il valore opposto (-x). In altre parole, matematicamente, una funzione è anche se soddisfa la seguente condizione:
![]()
Le funzioni pari sono un tipo di funzioni simmetriche, ora vediamo come appaiono le funzioni dispari.
funzioni strane
Le funzioni dispari sono funzioni simmetriche rispetto all’origine delle coordinate, cioè rispetto al punto (0,0).
Qui sotto puoi vedere graficamente una funzione dispari:
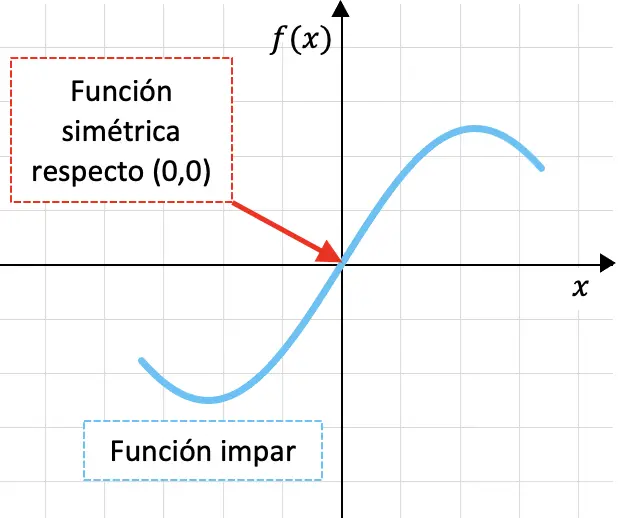
Il fatto che una funzione sia simmetrica rispetto all’origine delle coordinate significa che se pieghiamo il grafico della funzione prima attraverso l’asse OY e poi attraverso l’asse OX, il grafico della funzione si sovrapporrebbe.
Algebricamente, una funzione è dispari se è soddisfatta la seguente relazione tra le sue immagini:
![]()
Conoscere la simmetria di una funzione è molto utile per rappresentarla, perché conoscendo solo metà del grafico possiamo disegnare velocemente l’altra parte.
Come trovare la simmetria di una funzione
Per studiare la simmetria di una funzione, dobbiamo calcolare l’immagine di
![]()
, vale a dire che è necessario calcolare
![]()
Quindi, a seconda del risultato dell’immagine, la simmetria della funzione sarà:
- se è pieno
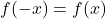
, la funzione è pari e quindi simmetrica rispetto all’asse Y.
- se è pieno
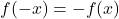
, la funzione è dispari e quindi simmetrica rispetto all’origine delle coordinate.
- Se nessuna delle condizioni precedenti è soddisfatta, è una funzione asimmetrica (non ha un asse di simmetria).
Ad esempio, analizziamo la simmetria della seguente funzione cubica:
![]()
Per studiare la simmetria della funzione, calcoliamo
![]()
![]()
L’espressione algebrica risultante è equivalente all’espressione della funzione originale ma ha cambiato segno o, in altre parole, è soddisfatta la seguente uguaglianza:
![]()
La funzione è quindi dispari e quindi simmetrica rispetto all’origine delle coordinate (0,0).
Proprietà delle funzioni simmetriche
Le funzioni simmetriche hanno le seguenti caratteristiche:
- La somma di due funzioni pari/dispari è uguale a un’altra funzione pari/dispari.
- Il prodotto di due funzioni pari o di due funzioni dispari dà una funzione pari.
- La derivata di una funzione pari/dispari è una funzione pari/dispari.
- La composizione tra due funzioni pari/dispari equivale a una funzione pari/dispari.
- L’unica funzione che è allo stesso tempo pari e dispari, cioè simmetrica rispetto all’asse OY e rispetto all’origine, è la funzione
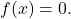
Risolti problemi di simmetria di una funzione
Esercizio 1
Trova la simmetria della seguente funzione:
![]()
Per calcolare la simmetria della funzione, dobbiamo valutare
![]()
![]()
Qualsiasi potenza di un numero negativo elevata a un esponente dà un numero positivo, quindi in questo caso è vera la seguente equazione:
![]()
La funzione è quindi pari e, quindi, è simmetrica rispetto all’asse y (asse Y).
Esercizio 2
Studia la simmetria della seguente funzione razionale:
![]()
Per determinare la simmetria della funzione, lo facciamo
![]()
![]()
In questo problema non è soddisfatta alcuna condizione di simmetria, perché l’immagine di
![]()
non è uguale a
![]()
né a
![]()
![]()
La funzione quindi non ha un asse di simmetria, ma è piuttosto una funzione asimmetrica.
Esercizio 3
Calcola la simmetria della seguente funzione:
![]()
Per analizzare la simmetria della funzione, dobbiamo calcolare
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f(-x)&=2(-x)|(-x)|\\[2ex]&=-2x|-x|\\[2ex]&=-2x|x|\\[2ex]&=-(2x|x|)\\[2ex]&=-f(x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d939238f353c0ab70492a66466dd0569_l3.png)
In questo caso, l’espressione risultante è come l’espressione originale ma con un cambio di segno, quindi è soddisfatta la seguente equazione:
![]()
La funzione è quindi dispari e quindi simmetrica rispetto all’origine delle coordinate (0,0).