In questa pagina troverai la definizione di sezioni coniche, perché sono così importanti e i diversi tipi di sezioni coniche che esistono (cerchio, ellisse, iperbole e parabola). Inoltre, sarai in grado di vedere le differenze tra le loro equazioni.
Cosa sono le sezioni coniche?
Nella geometria analitica, le sezioni coniche (o semplicemente coniche) sono tutte le curve risultanti dalle diverse intersezioni tra un cono e un piano, quando questo piano non passa per il vertice del cono. Esistono quattro tipi di sezioni coniche: la circonferenza, l’ellisse, la parabola e l’iperbole.
Di seguito le 4 possibili sezioni ottenibili da qualsiasi cono:
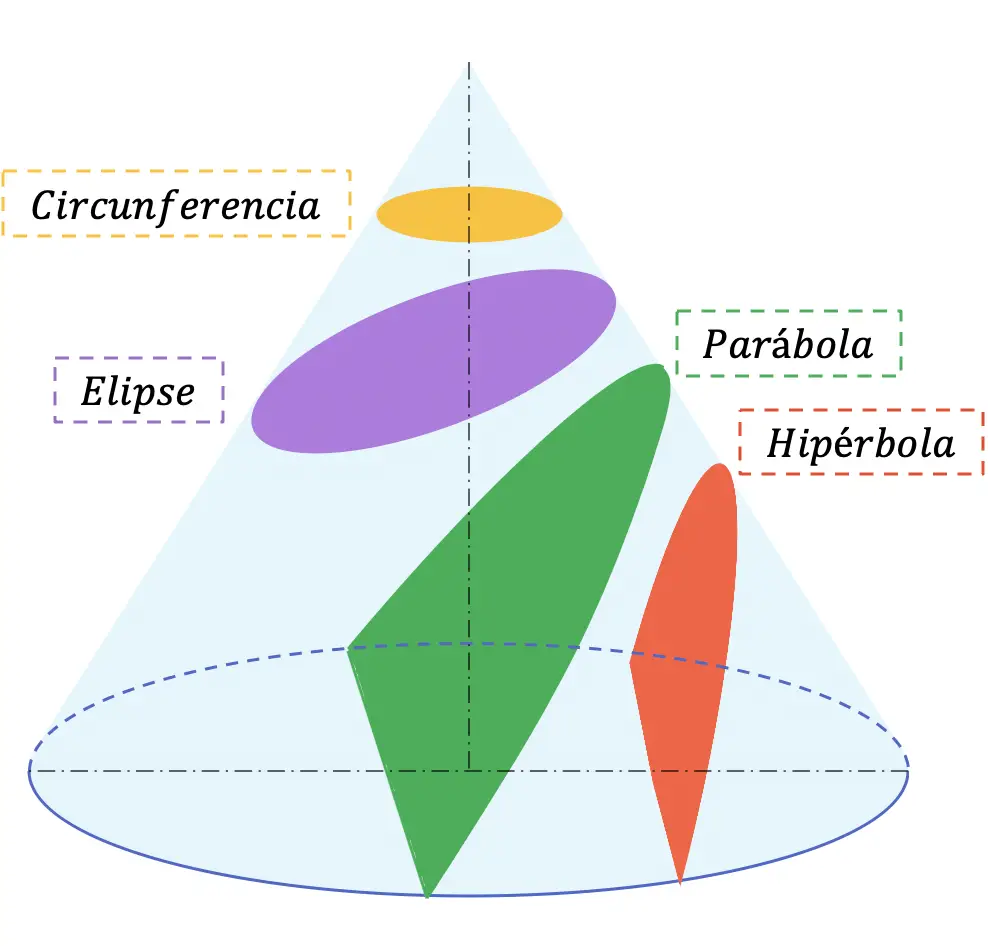
Le sezioni coniche vengono generalmente studiate nella scuola secondaria (Bachillerato), nelle materie di matematica e disegno tecnico.
Tipi di sezioni coniche
Una volta visto il concetto di sezione conica, vediamo quali sono i quattro tipi di sezioni coniche esistenti: il cerchio, l’ellisse, la parabola e l’iperbole.
circonferenza
La circonferenza è una sezione conica che si ottiene tagliando un cono con un piano perpendicolare al suo asse di rivoluzione (parallelo alla base).

Inoltre la circonferenza è il luogo dei punti del piano equidistanti da un punto fisso detto centro.
Ellisse
L’ellisse è una linea piatta, chiusa, curva, molto simile alla circonferenza, ma la sua forma è più ovale. In particolare, risulta dal taglio della superficie di un cono mediante un piano obliquo il cui angolo rispetto all’asse di rivoluzione è maggiore di quello del generatore.
Inoltre, tutti i punti di un’ellisse soddisfano una condizione: l’ellisse è il luogo di tutti i punti di un piano la cui somma delle distanze da altri due punti fissi (detti fuochi F e F’) è costante.

Parabola
In matematica, una parabola è il luogo dei punti del piano equidistanti da un punto fisso (chiamato fuoco) e da una linea fissa (chiamata direttrice).

Geometricamente la parabola è il risultato della sezione di un cono mediante un piano avente un angolo di inclinazione rispetto all’asse di rivoluzione equivalente all’angolo della generatrice del cono. Pertanto il piano contenente la parabola è parallelo alla generatrice del cono.
Una caratteristica molto importante di questa sezione conica è l’ equazione della parabola , perché a seconda del suo stato ci permette di identificare di che tipo di parabola si tratta. In questo link troverai tutte le equazioni della parabola, quali sono gli elementi della parabola, le loro proprietà, esempi, esercizi risolti,… tra le altre caratteristiche delle parabole.
Iperbole
Essendo una sezione conica, un’iperbole si ottiene quando un cono è tagliato da un piano con un angolo minore dell’angolo formato dalla generatrice del cono rispetto al suo asse di rivoluzione.
Matematicamente, un’iperbole può essere definita come il luogo dei punti del piano che soddisfano la seguente proprietà: il valore assoluto della differenza delle distanze tra un punto qualsiasi dell’iperbole e due punti fissi (detti fuochi) deve essere costante.
Inoltre, il valore della sottrazione di queste due distanze è sempre equivalente alla distanza tra i due vertici dell’iperbole.
![]()

Come sono sicuro che tu abbia già dedotto, il valore del parametro
![]()
di un’iperbole è fondamentale per le iperboli. Nel link seguente puoi vedere la nostra spiegazione dell’iperbole, dove troverai perché è un coefficiente così importante e quali sono tutti gli elementi che caratterizzano un’iperbole. Inoltre, troverai l’aspetto dell’equazione di un’iperbole , i diversi tipi di iperboli esistenti e persino problemi ed esercizi passo passo sulle iperboli.
Equazione generale delle sezioni coniche
Ciascuna sezione conica può essere espressa analiticamente come un’equazione. Infatti tutte le equazioni coniche devono essere di secondo grado:
![]()
Di conseguenza, almeno uno dei coefficienti
![]()
O
![]()
della formula deve essere diverso da zero.
Pertanto, a seconda dei valori dei parametri, l’equazione corrisponderà a un tipo di conica o a un altro:
- Circonferenza : per l’equazione generale che descrive una circonferenza, i termini

E

deve corrispondere e

deve essere zero.
![]()
- Ellisse : L’equazione corrisponderà all’espressione matematica di un’ellisse quando è verificata la seguente condizione:
![]()
- Parabola : affinché l’equazione sia una parabola, deve essere soddisfatta la seguente uguaglianza:
![]()
- Iperbole : Infine, l’equazione generale di un’iperbole deve soddisfare la seguente disuguaglianza:
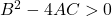 Navigazione articoli
Navigazione articoli