▷ Come eseguire la scomposizione polinomiale di un numero ✅

In questa pagina spieghiamo come eseguire la scomposizione (o espressione) polinomiale di un numero. Qui puoi vedere esempi di scomposizioni polinomiali e, inoltre, troverai esercizi passo passo risolti per esercitarti.

Cos’è la scomposizione polinomiale di un numero?

In matematica, la scomposizione polinomiale di un numero consiste nell’esprimere quel numero in una somma, in modo tale che ciascun termine della somma sia il prodotto di ciascuna cifra del numero per una potenza di base 10.

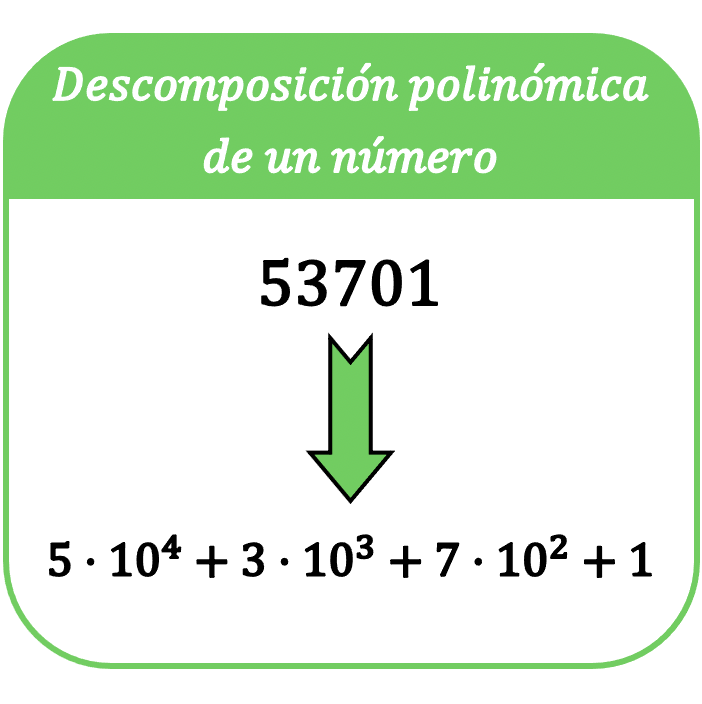
Il termine scomposizione polinomiale di un numero è noto anche come espressione polinomiale di un numero .

Come eseguire una scomposizione polinomiale

Per eseguire la scomposizione polinomiale di un numero, è necessario moltiplicare ciascuna cifra del numero per 10 elevato al numero di cifre a destra .

Ad esempio, se vogliamo calcolare la scomposizione polinomiale del seguente numero:

$86293$

In questo caso il numero 8 occupa la quinta posizione, quindi ha 4 cifre alla sua destra. Dobbiamo quindi moltiplicare otto per dieci alla potenza di quattro:

$8\cdot 10^4$

Quindi, per scomporre polinomialmente il numero 86293 bisogna fare lo stesso con tutte le cifre del numero, ed esprimere tutte le moltiplicazioni sotto forma di somma:

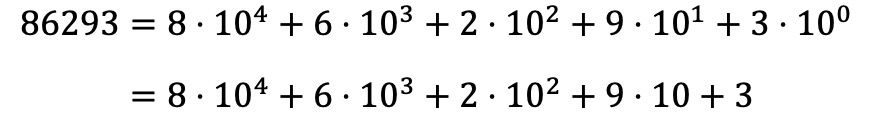
Si noti che la potenza 10 ⁰ scompare perché, secondo le proprietà delle potenze, qualsiasi numero elevato a 0 è uguale a 1, quindi 10 ⁰ =1.

D’altra parte, puoi anche trovare la scomposizione polinomiale di un numero dalla sua scomposizione moltiplicativa:

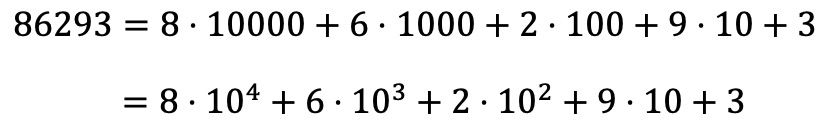
Scomposizione polinomiale dei numeri naturali per la scuola primaria

Esempi di scomposizioni polinomiali di numeri

Una volta visto come si effettua la scomposizione polinomiale di un numero, vedremo diversi esempi di questo tipo di operazioni per comprendere appieno il concetto.

Scomposizione polinomiale di 3641:

$3641 = 3\cdot 10^3 +6 \cdot 10^2 + 4\cdot 10 + 1$

Scomposizione polinomiale di 56912:

$56912 = 5\cdot 10^4 +6\cdot 10^3 +9 \cdot 10^2 + 1\cdot 10 + 2$

Scomposizione polinomiale di 27084:

$\begin{aligned} 27084 &= 2\cdot 10^4 +7\cdot 10^3 +0\cdot 10^2 + 8\cdot 10 + 4 \\[2ex] & = 2\cdot 10^4 +7\cdot 10^3 + 8\cdot 10 + 4 \end{aligned}$

In quest’ultimo esempio, possiamo semplificare la terza moltiplicazione poiché qualsiasi numero moltiplicato per zero si annulla.

Scomposizione polinomiale dei numeri decimali

Abbiamo appena visto come eseguire la scomposizione polinomiale dei numeri naturali. Ma… come si scompone polinomialmente un numero decimale?

Ebbene, la scomposizione polinomiale con i numeri decimali si fa allo stesso modo degli interi ma, in più, aggiungiamo il prodotto di ciascuna cifra decimale moltiplicato per una potenza in base 10 il cui esponente è la posizione decimale occupata da detta cifra con un negativo cartello.

Spiegato a parole può sembrare molto complicato, ma vedrai che con un esempio si capisce meglio:

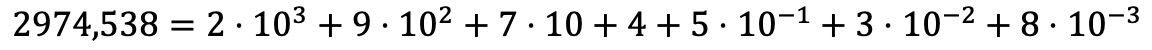
Esercizi di scomposizione polinomiale risolti

Affinché tu possa esercitarti con le scomposizioni polinomiali, abbiamo preparato diversi esercizi risolti passo dopo passo.

Non dimenticare che puoi farci tutte le domande che hai nei commenti! 🤔🤔🤔

Esercizio 1

Esegui la scomposizione polinomiale dei seguenti numeri:

$\text{A)} \ 7935$

$\text{B)} \ 1548$

$\text{C)} \ 55476$

$\text{D)} \ 287694$

Vedi la soluzione

Per trovare la scomposizione polinomiale di qualsiasi numero, moltiplica ciascuna cifra di quel numero per 10 per il numero di cifre a destra, quindi somma tutte le moltiplicazioni. Ancora:

$\text{A)} \ 7935 = 7 \cdot 10^3+ 9\cdot 10^2 +3 \cdot 10 +5$

$\text{B)} \ 1548 = 1 \cdot 10^3+ 5\cdot 10^2 +4 \cdot 10 +8$

$\text{C)} \ 55476 = 5\cdot 10^4+ 5 \cdot 10^3+ 4\cdot 10^2 +7\cdot 10 +6$

$\text{D)} \ 287694 = 2\cdot 10^5+8\cdot 10^4+ 7 \cdot 10^3+ 6\cdot 10^2 +9\cdot 10 +4$

Esercizio 2

Trova la scomposizione polinomiale dei seguenti numeri:

$\text{A)} \ 461$

$\text{B)} \ 3030$

$\text{C)} \ 11950$

$\text{D)} \ 8741866$

Vedi la soluzione

Per scomporre polinomialmente un numero, devi moltiplicare ciascuna cifra di detto numero per dieci per il numero di cifre alla sua destra, quindi sommare tutti i prodotti. Ancora:

$\text{A)} \ 461 = 4\cdot 10^2 +6 \cdot 10 +1$

$\text{B)} \ \begin{aligned} 3030 & = 3 \cdot 10^3+ 0\cdot 10^2 +3 \cdot 10 +0 \\[2ex] &= 3 \cdot 10^3+3 \cdot 10 \end{aligned}$

$\text{C)} \ 11950 = 1\cdot 10^4+ 1 \cdot 10^3+ 9\cdot 10^2 +5\cdot 10$

$\text{D)} \ 8741866 = 8\cdot 10^6+7\cdot 10^5+4\cdot 10^4+ 1 \cdot 10^3+ 8\cdot 10^2 +6\cdot 10 +6$

Esercizio 3

Calcola la scomposizione polinomiale dei seguenti numeri decimali:

$\text{A)} \ 51,63$

$\text{B)} \ 249,99$

$\text{C)} \ 0,82694$

$\text{D)} \ 5,7201$

Vedi la soluzione

In questo problema tutti i numeri sono decimali, quindi per scomporli devi moltiplicare ogni cifra non decimale per 10 elevata al numero di cifre che ha fino alla virgola decimale, e moltiplicare ogni cifra decimale per 10 elevata alla sua posizione decimale con un segno negativo.

$\text{A)} \ 51,63 = 5 \cdot 10 +1 + 6 \cdot 10^{-1} +3 \cdot 10^{-2}$

$\text{B)} \ 249,99 = 2\cdot 10^2 + 4 \cdot 10 +9 + 9 \cdot 10^{-1} +9 \cdot 10^{-2}$

$\text{C)} \ \begin{aligned} 0,82694 & = 0 + 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\\[2ex] & = 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\end{aligned}$

$\text{D)} \ \begin{aligned} 5,7201 & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+0\cdot 10^{-3}+1\cdot 10^{-4}\\[2ex] & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+1\cdot 10^{-4} \end{aligned}$

Scomposizione (o espressione) polinomiale di un numero

Cos’è la scomposizione polinomiale di un numero?

Come eseguire una scomposizione polinomiale

Esempi di scomposizioni polinomiali di numeri

Scomposizione polinomiale dei numeri decimali

Esercizi di scomposizione polinomiale risolti

Esercizio 1

Esercizio 2

Esercizio 3

Lascia un commento Annulla risposta