In questa pagina spieghiamo come applicare la regola di Ruffini per dividere i polinomi. Oltre alla spiegazione, potrai vedere esempi ed esercizi risolti passo passo sulle divisioni dei polinomi con la regola di Ruffini. Inoltre troverai tutte le applicazioni di questo metodo e, in effetti, più di una ti sorprenderà sicuramente.
Qual è la regola di Ruffini?
In matematica, la regola di Ruffini è un metodo algebrico che consente di dividere rapidamente qualsiasi polinomio per polinomi della forma xr . La regola di Ruffini prende il nome dal matematico Paolo Ruffini, che inventò questo metodo.
Tuttavia, la regola di Ruffini non viene utilizzata solo per dividere i polinomi, ma ha molti altri usi. Ad esempio, la regola di Ruffini viene utilizzata anche per trovare le radici di un polinomio, per trovare il valore numerico di un polinomio, per fattorizzare un polinomio o anche per risolvere equazioni di terzo grado o superiori. Di seguito vedremo come viene applicata la regola di Ruffini per poter effettuare tutte queste operazioni.
Infine, la regola di Ruffini è conosciuta anche come metodo di Ruffini, teorema di Ruffini o divisione sintetica dei polinomi.
Come applicare la regola di Ruffini
Come abbiamo visto, l’utilizzo principale della regola di Ruffini è quello di dividere un polinomio per un binomio, cioè di effettuare una divisione del seguente tipo:
![]()
Si noti che per utilizzare la regola di Ruffini , il polinomio di divisione deve essere sempre formato da una x (con coefficiente pari a 1) e un numero (positivo o negativo), altrimenti non è possibile utilizzare l’algoritmo di Ruffini.
Per applicare la regola di Ruffini è necessario seguire tutta una procedura, quindi di seguito risolveremo un esempio passo dopo passo per vedere come viene applicata la regola di Ruffini (o metodo Ruffini).
Esempio della regola di Ruffini
- Risolvi la seguente divisione di polinomi utilizzando la regola di Ruffini:
![]()
Innanzitutto bisogna disegnare due rette perpendicolari che si intersecano tra loro, quindi posizionare il dividendo e il divisore come segue:
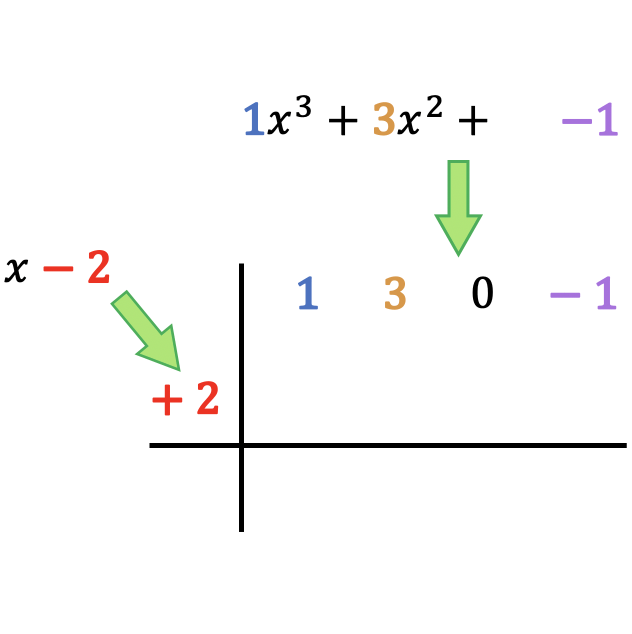
Come puoi vedere, dobbiamo mettere in alto i coefficienti del polinomio divisore, ordinati dal grado più alto al più basso, e posizioniamo il termine indipendente del polinomio divisore a sinistra della casella con cambio di segno .
Attenzione: se il polinomio dei dividendi non ha un termine di un certo grado (polinomio incompleto), al suo posto viene messo uno 0. Ad esempio, in questo caso il polinomio
![]()
Non ha un monomio di grado 1, quindi mettiamo uno 0 al suo posto.
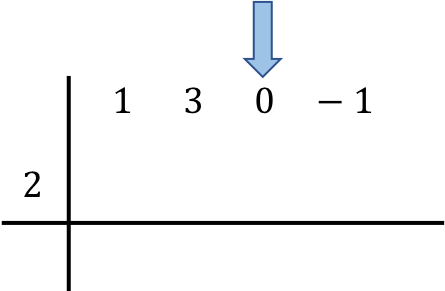
Una volta posizionati i polinomi coinvolti nell’operazione abbassiamo il primo numero direttamente sulla riga sottostante:
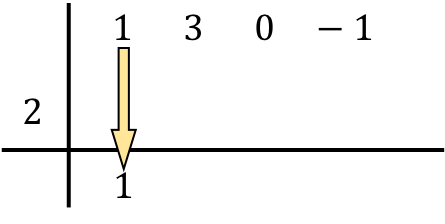
Ora arriva il passaggio che caratterizza la regola di Ruffini: moltiplichiamo il numero sottostante per il numero a sinistra e posizioniamo il risultato nella colonna seguente :
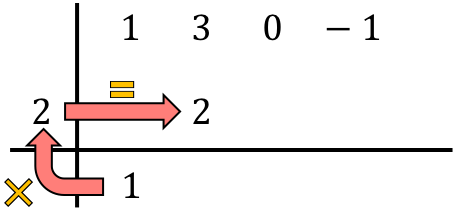
E aggiungiamo i numeri nella colonna, mettendo il risultato della somma subito sotto:
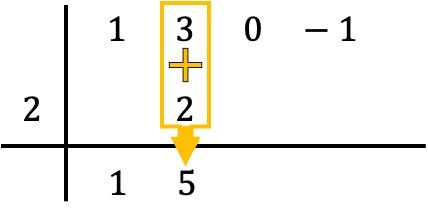
Quindi il metodo di Ruffini prevede la ripetizione di questo processo. Quindi facciamo di nuovo la stessa cosa: moltiplichiamo il numero in basso per il numero a sinistra, inseriamo il risultato nella colonna successiva e, infine, aggiungiamo i numeri allineati verticalmente:
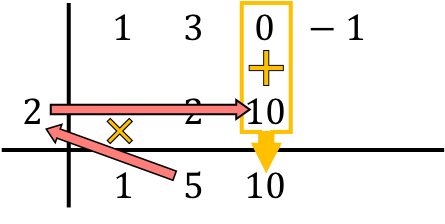
E ripetiamo la stessa procedura successivamente fino alla fine. Per prima cosa facciamo il prodotto del numero sottostante per il numero a sinistra, poi inseriamo il risultato nella colonna successiva e, infine, aggiungiamo i numeri nella stessa colonna:
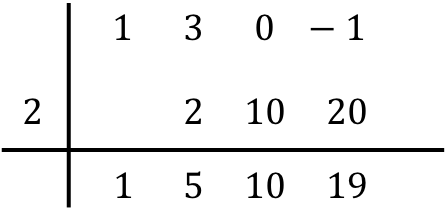
Quindi, quando avremo riempito tutte le colonne, significa che abbiamo finito di dividere i polinomi.
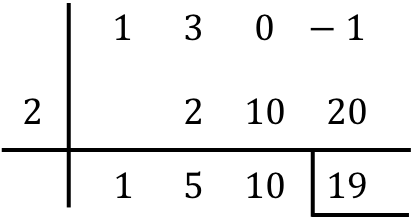
Quindi devi solo trovare il risultato della divisione dei polinomi:
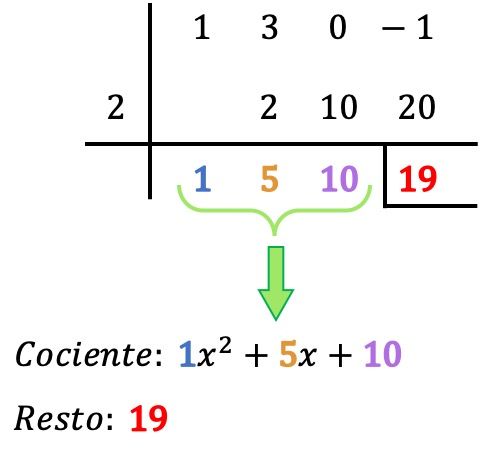
- Il resto della divisione tra i due polinomi è l’ultimo numero della riga sottostante, quindi nel nostro caso il resto è pari a 19. Solitamente il resto viene indicato posizionando una barra a sinistra ed un’altra sotto detto numero.
- Il quoziente della divisione polinomiale è determinato dagli altri valori ottenuti, che sono i coefficienti del quoziente polinomiale. La prima cifra da destra corrisponde al coefficiente del termine di grado 0, la cifra successiva è il coefficiente del termine di grado 1, la successiva al grado 2, la successiva al grado 3,… e così via fino alla fine. . COSÌ:
Esercizi risolti della regola di Ruffini
Di seguito troverai diversi esercizi risolti passo passo sulla regola di Ruffini in modo che tu possa esercitarti e capire come risolvere le divisioni di polinomi con questo metodo. Ti consigliamo di provare ogni esercizio e poi verificare se lo hai eseguito correttamente osservando la correzione.
Esercizio 1
Esegui la seguente divisione dei polinomi con la regola di Ruffini:
![]()
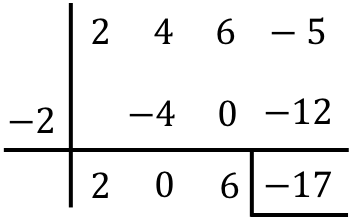
Il risultato della divisione tra i due polinomi è quindi:
Quoziente:
![]()
Riposo:
![]()
Esercizio 2
Calcola la seguente divisione dei polinomi utilizzando la regola di Ruffini:
![]()
In questo caso particolare il polinomio dei dividendi non ha un termine di secondo grado, dobbiamo quindi mettere uno zero al suo posto:
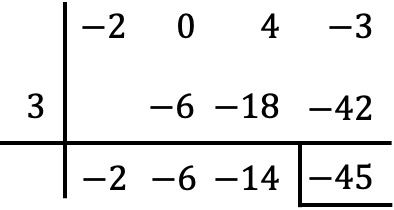
Il risultato della divisione tra i 2 polinomi è quindi:
Quoziente:
![]()
Riposo:
![]()
Esercizio 3
Trova il risultato della seguente divisione dei polinomi secondo la regola di Ruffini:
![]()
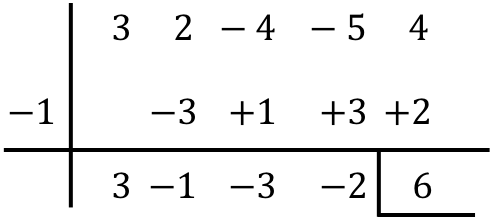
In conclusione, il risultato della divisione dei due polinomi è:
Quoziente:
![]()
Riposo:
![]()
Esercizio 4
Trova il valore dell’incognita m tale che il resto della seguente divisione dei polinomi sia equivalente a 5:
![]()
Poiché il divisore è della forma (xr) o (x+r), possiamo applicare la regola di Ruffini per risolvere la divisione. Applichiamo quindi il metodo di Ruffini trascinando l’incognita m:
Ora uguagliamo il resto ottenuto a 5, perché il resto deve essere 5:
![]()
E risolviamo l’equazione per trovare il valore del parametro m :
![]()
![]()
Quindi, quando la variabile m equivale a 3, il resto della divisione tra i polinomi sarà pari a 5.
Esercizio 5
Determina il valore del parametro m in modo che il resto della seguente divisione polinomiale dia 3:
![]()
Poiché il divisore è della forma (xr) o (x+r), possiamo applicare la regola di Ruffini per risolvere la divisione. Utilizziamo quindi il metodo di Ruffini trascinando l’incognita m:
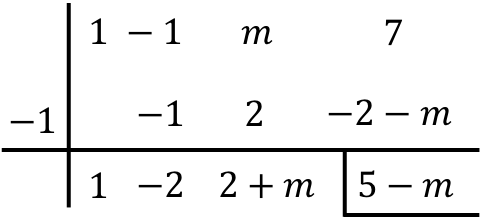
Tieni presente la proprietà distributiva durante l’ultima moltiplicazione:
![]()
D’altra parte, il calcolo del resto della divisione è:
![]()
![]()
![]()
Ora uguagliamo l’espressione del resto risultante a 3, poiché il resto della divisione deve essere uguale a 3:
![]()
E risolviamo l’equazione risultante per determinare il valore del parametro m :
![]()
![]()
![]()
![]()
Pertanto, m deve essere uguale a 2 affinché il resto della divisione polinomiale sia uguale a 3.
Altre applicazioni della regola di Ruffini
Come spiegato, la regola di Ruffini viene utilizzata principalmente per eseguire divisioni tra polinomi. Tuttavia la regola di Ruffini viene utilizzata anche per eseguire altri calcoli, li vedremo di seguito.
Radici di un polinomio
Le radici di un polinomio possono essere facilmente determinate utilizzando la regola di Ruffini. Se non sai qual è la radice di un polinomio, rivediamo la sua definizione:
Le radici (o zeri) di un polinomio sono i valori che annullano il polinomio. O in altre parole, le radici di un polinomio sono tutti quei valori che valutati nel polinomio hanno un valore numerico pari a 0.
![]()
Sappiamo invece grazie al teorema dei resti che se il valore numerico di un polinomio per un dato valore
![]()
è zero, necessariamente il resto della divisione di detto polinomio tra
![]()
Deve anche essere 0.
![]()
Pertanto, se usi la regola di Ruffini per dividere un polinomio
![]()
tra un altro polinomio della forma
![]()
otteniamo un resto pari a 0, questo significa che
![]()
è una radice del polinomio
![]()
Con un esempio capiremo sicuramente meglio:
- Controlla se
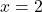
è una radice del polinomio
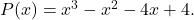
Per verificare se il valore dato è una radice del polinomio è sufficiente applicare il metodo Ruffini con detto polinomio e detto valore:
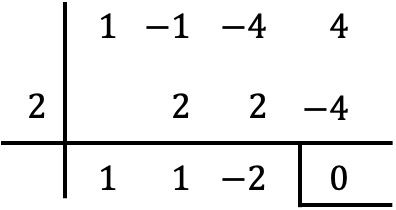
Poiché il resto ottenuto con la regola di Ruffini è pari a zero, ciò significa effettivamente proprio così
![]()
è una radice del polinomio
![]()
Fattorizzare i polinomi
La regola di Ruffini è il metodo solitamente applicato ai polinomi fattoriali, perché permette di conoscere velocemente tutte le radici di un polinomio di grado 3, 4, 5, ecc.
Vediamo quindi come fattorizzare un polinomio con l’algoritmo di Ruffini utilizzando un esempio:
- Fattorizza il seguente polinomio di terzo grado:
![]()
La prima cosa da fare è trovare tutte le radici del polinomio. E le possibili radici di un polinomio sono i divisori del termine indipendente, che in questo caso è 6. Quindi:
Possibili radici del polinomio: +1, -1, +2, -2, +3, -3, +6, -6
Bisogna ora provare a dividere il polinomio tra ciascuno di questi valori con la regola di Ruffini. Se il resto della divisione è 0 significa che il valore è radice del polinomio; tuttavia, se il resto della divisione è diverso da 0, il valore non è la radice del polinomio. Pertanto, testare la regola di Ruffini con tutti i numeri cancella il resto solo nei seguenti tre casi:
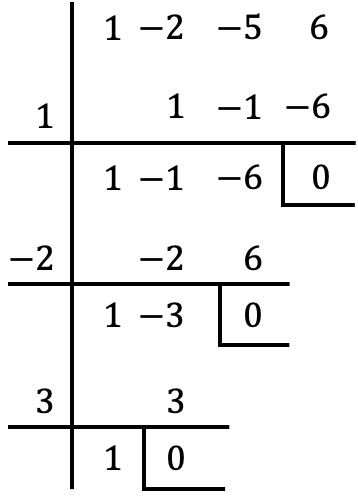
Pertanto le radici del polinomio nel problema sono i valori con i quali il resto si annulla, ovvero:
![]()
Infine, per fattorizzare il polinomio dobbiamo esprimere ciascuna radice
![]()
sotto forma di un fattore del tipo
![]()
, vale a dire che per ogni radice bisogna mettere una parentesi con a
![]()
e la radice trovata ha cambiato segno:
![]()
Come puoi vedere, abbiamo scomposto con successo il polinomio utilizzando la regola di Ruffini. Tuttavia, potresti aver avuto dei dubbi sulla fattorizzazione dei polinomi perché è un argomento molto complesso. In questo caso puoi cercare sul nostro sito web (nel motore di ricerca in alto a destra) l’articolo che abbiamo su come fattorizzare i polinomi , lì lo spieghiamo in modo più dettagliato e puoi esercitarti con gli esercizi risolti passo dopo passo. Inoltre, ti mostriamo anche altri metodi per fattorizzare i polinomi.
Calcolare il valore numerico di un polinomio
Anche se può sembrare sorprendente, il valore numerico di un polinomio può essere determinato dalla regola di Ruffini utilizzando il teorema dei resti.
Ma ovviamente per fare questo è necessario conoscere il teorema del resto. Se così non fosse, puoi cercare la spiegazione del teorema del resto sul nostro sito (nel motore di ricerca in alto a destra) .
Quindi, grazie al teorema dei resti, possiamo conoscere il valore numerico di qualsiasi polinomio. Vediamo come farlo utilizzando un esempio:
- Calcolare il valore numerico di

Per
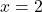
applicando la regola di Ruffini, l’essere
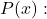
![]()
Per trovare il valore numerico del polinomio per il valore
![]()
L’unica cosa che dobbiamo fare è usare la regola di Ruffini con il polinomio e detto valore:
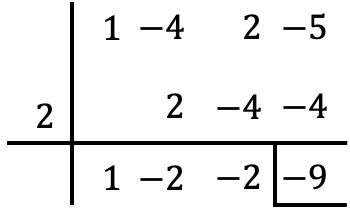
Quindi, dal teorema del resto, sappiamo che il valore numerico del polinomio coincide con il resto della divisione del polinomio . Pertanto, il valore numerico del polinomio in
![]()
è -9.
![]()
Possiamo invece verificare che la regola di Ruffini sia applicata correttamente calcolando numericamente il valore numerico:
![Rendered by QuickLaTeX.com \begin{aligned} P(2) &= 2^3-4\cdot 2^2+2\cdot 2-5\\[2ex] &= 8-4\cdot 4+2\cdot 2-5 \\[2ex] & = 8-16+4-5 \\[2ex] & =\bm{-9} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c935b3276a3915dbdf93755851ef28e5_l3.png)
Risolvere equazioni di terzo grado o superiori
Un’altra applicazione della regola di Ruffini è quella di risolvere equazioni di grado maggiore di 2, poiché in questi casi non esiste la formula come nell’equazione di secondo grado. Vediamo come farlo utilizzando un esempio:
- Risolvi la seguente equazione quadratica utilizzando la regola di Ruffini:
![]()
Dobbiamo trattare l’equazione come se fosse un polinomio. Successivamente dobbiamo calcolare tante radici del “polinomio” utilizzando la regola di Ruffini fino ad ottenere un’equazione di secondo grado . In questo caso si tratta di un’equazione di grado 3, è quindi sufficiente determinare una radice del “polinomio”:
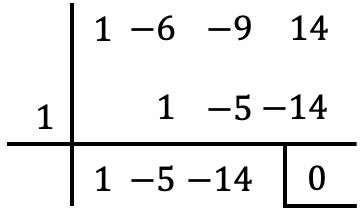
Una soluzione dell’equazione sarà quindi
![]()
Ebbene, per trovare le altre soluzioni dobbiamo porre pari a 0 il polinomio ottenuto nel quoziente della regola di Ruffini:
![]()
E ora risolviamo l’equazione quadratica risultante con la sua formula corrispondente:
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x = \cfrac{5 \pm 9}{2} = \begin{cases} \cfrac{5+9}{2} = \cfrac{14}{2} = 7 \\[4ex]\cfrac{5-9}{2} = \cfrac{-4}{2} = -2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a57aa9f04a1053566c6a53b65afa008a_l3.png)
In conclusione le 3 soluzioni dell’equazione di terzo grado sono:
![]()