Rappresentazione delle funzioni -

In questo articolo vedremo come rappresentare qualsiasi tipo di funzione su un grafico. Inoltre, troverai esercizi passo passo risolti sulla rappresentazione delle funzioni su un grafico.

Come rappresentare una funzione su un grafico

Per rappresentare una funzione su un grafico è necessario eseguire i seguenti passaggi:

Trova il dominio della funzione.
Calcolare i punti limite della funzione con gli assi cartesiani.
Calcolare gli asintoti della funzione.
Studia la monotonia della funzione e trova i suoi estremi relativi .
Studia la curvatura della funzione e trova i suoi punti di flesso .
Traccia i punti di interruzione, gli asintoti, gli estremi relativi e i punti di flesso, quindi traccia la funzione.

Esempio di rappresentazione di una funzione

Affinché tu possa vedere come è rappresentata graficamente una funzione, risolveremo passo dopo passo il seguente esercizio:

Traccia su un grafico la seguente funzione razionale:

$f(x)=\cfrac{x^2}{x-1}$

La prima cosa da fare è calcolare il dominio della funzione . Questa è una funzione razionale, quindi dobbiamo impostare il denominatore uguale a zero per vedere quali numeri non appartengono al dominio della funzione:

$x-1=0$

$x=1$

Quindi, quando x è 1, il denominatore sarà 0 e quindi la funzione non esisterà. Il dominio della funzione è quindi costituito da tutti i numeri reali tranne x=1.

$\text{Dom } f= \mathbb{R}-\{1 \}$

Per trovare il punto di intersezione con l’asse X , dobbiamo risolvere l’equazione

$f(x)= 0.$

Poiché la funzione ha sempre un valore pari a 0 sull’asse X:

$f(x)=0$

$\cfrac{x^2}{x-1} = 0$

Il termine

$x -1$

Ciò comporta la divisione dell’intero lato sinistro, quindi possiamo moltiplicarlo per l’intero lato destro:

$x^2 = 0 \cdot (x-1)$

$x^2 = 0$

$x = 0$

Il punto di intersezione con l’asse OX è quindi:

$\bm{(0,0)}$

E per trovare il punto di intersezione con l’asse Y , calcoliamo

$f(0).$

Poiché x è sempre 0 sull’asse Y:

$f(0)=\cfrac{0^2}{0-1} = \cfrac{0}{-1} = 0$

Pertanto, il punto di taglio con l’asse OY è:

$\bm{(0,0)}$

In questo caso, quando la funzione passa per l’origine delle coordinate, il punto di intersezione con l’asse X coincide con il punto di intersezione con l’asse Y.

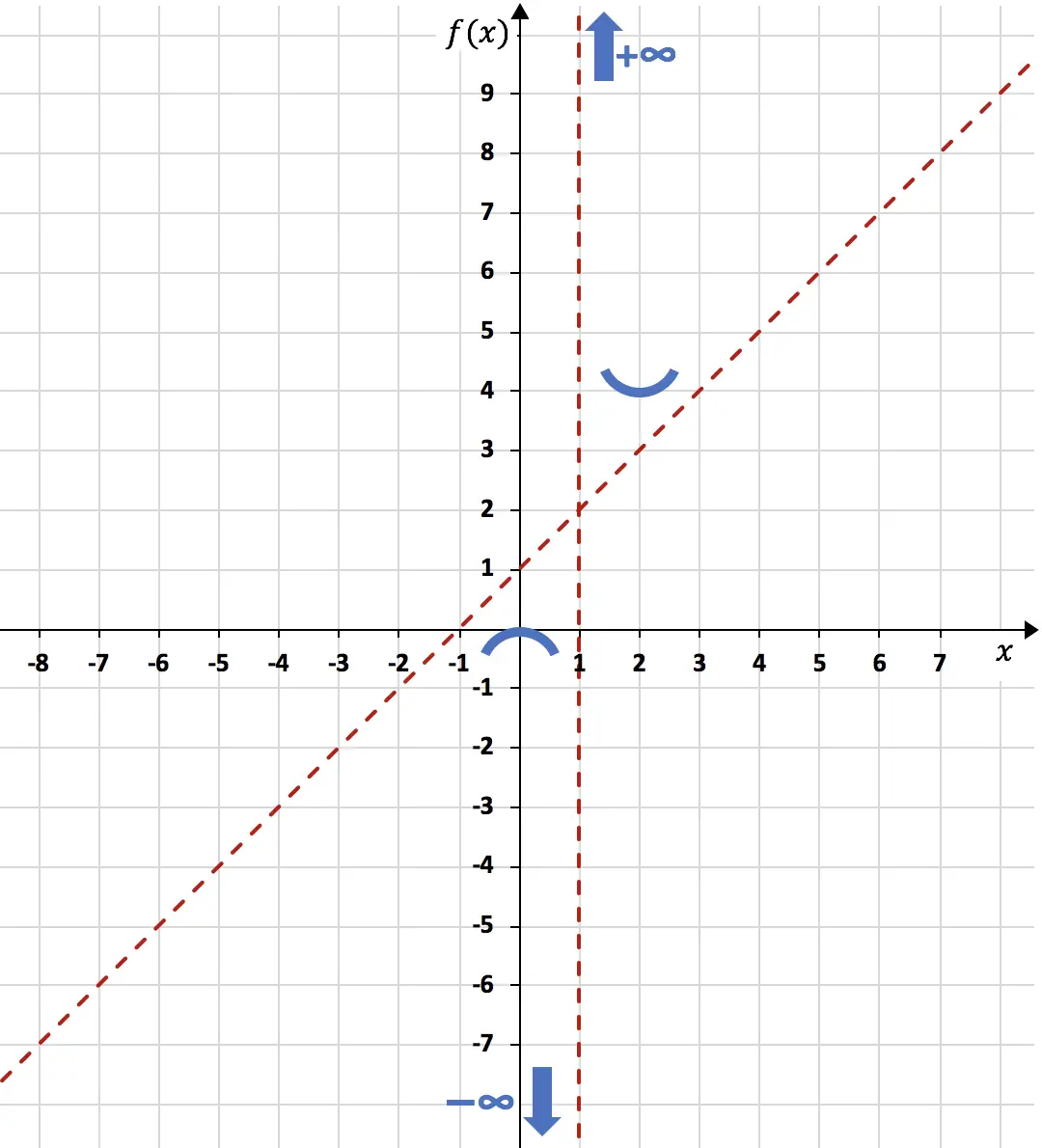
Una volta che conosciamo il dominio e i punti limite, dobbiamo calcolare gli asintoti della funzione .

Per vedere se la funzione ha asintoti verticali, dobbiamo calcolare il limite della funzione nei punti che non appartengono al dominio (in questo caso x=1). E se il risultato è infinito, è un asintoto verticale. Ancora:

$\displaystyle \lim_{x \to 1} \ \cfrac{x^2}{x-1} = \cfrac{1^2}{1-1} = \cfrac{1}{0} = \infty$

Poiché il limite della funzione quando x tende a 1 dà infinito, x=1 è un asintoto verticale:

rappresentare funzioni, asintoto verticale

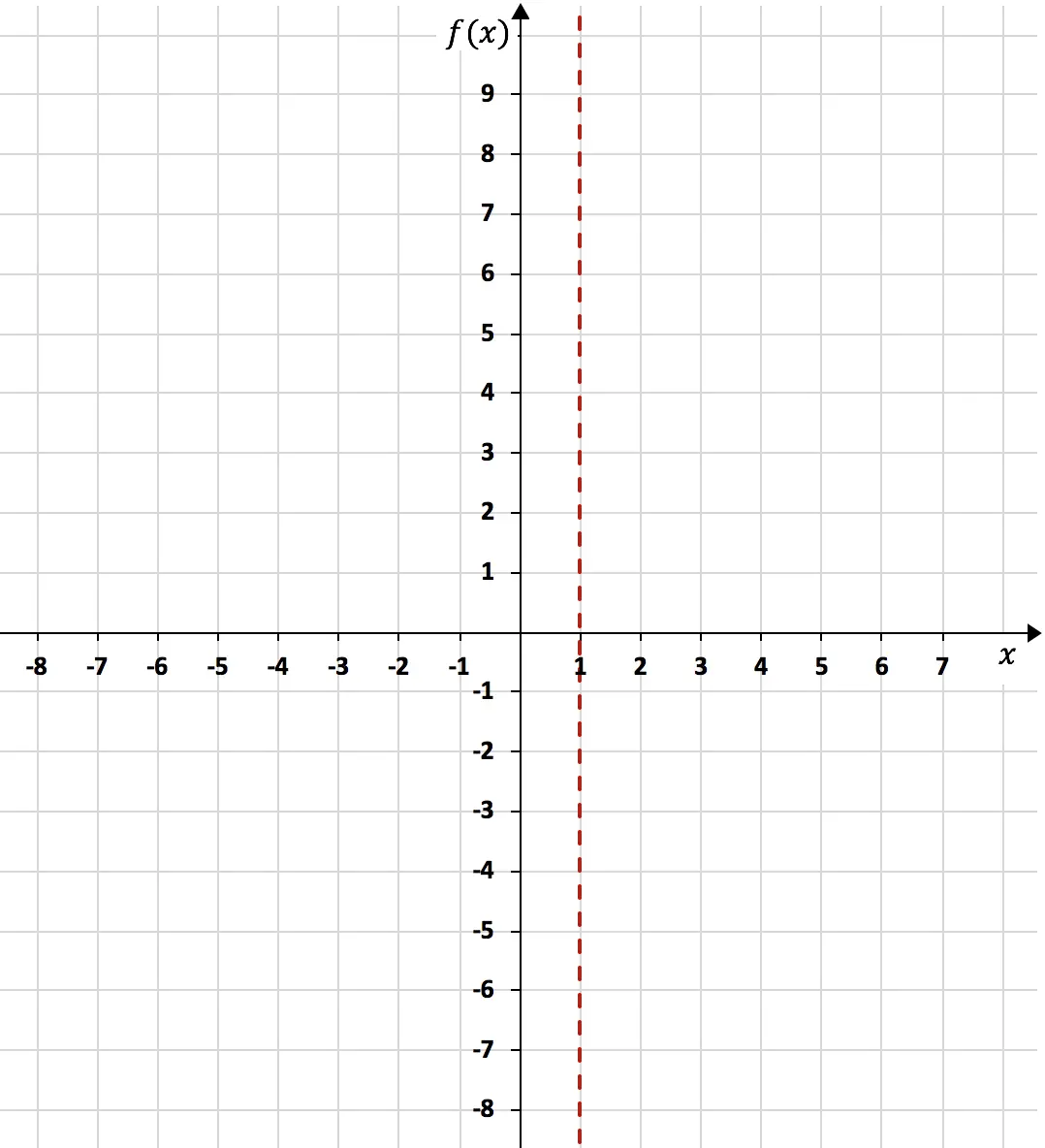
Una volta calcolato l’asintoto verticale è necessario calcolare i limiti laterali della funzione rispetto ad esso. Poiché non sappiamo se la funzione tenderà a -∞ o +∞ quando si avvicina a x=1 da sinistra, e non sappiamo quando si avvicina a x=1 da destra.

Procediamo quindi a calcolare il limite laterale sinistro della funzione in x=1:

$\displaystyle \lim_{x \to 1^{-}} \cfrac{x^2}{x-1}$

Per calcolare numericamente il limite laterale in un punto, dobbiamo sostituire nella funzione un numero che è molto vicino al punto. In questo caso, vogliamo un numero molto vicino a 1 a sinistra, come 0,9. Sostituiamo quindi il punto 0.9 nella funzione:

$\cfrac{0,9^2}{0,9-1}=\cfrac{0,81}{-0,1}=-81$

I limiti laterali ad un asintoto possono dare solo +∞ o -∞. E poiché sostituendo nella funzione un numero molto vicino a 1 a sinistra abbiamo ottenuto un risultato negativo, il limite a sinistra è -∞:

$\displaystyle \lim_{x \to 1^{-}} \cfrac{x^2}{x-1} = \bm{-\infty}$

Ora eseguiamo la stessa procedura con il confine del lato destro:

$\displaystyle \lim_{x \to 1^{+}} \cfrac{x^2}{x-1}$

Sostituiamo un numero molto vicino a 1 a destra nella funzione. Ad esempio il punto 1.1:

$\cfrac{1,1^2}{1,1-1}=\cfrac{1,21}{0,1}=+12,1$

In questo caso, il risultato del limite laterale è un numero positivo. Il limite a destra è quindi +∞:

$\displaystyle \lim_{x \to 1^{+}} \cfrac{x^2}{x-1} = \bm{+\infty}$

In conclusione, per x=1 la funzione tende verso meno infinito a sinistra, e più infinito a destra:

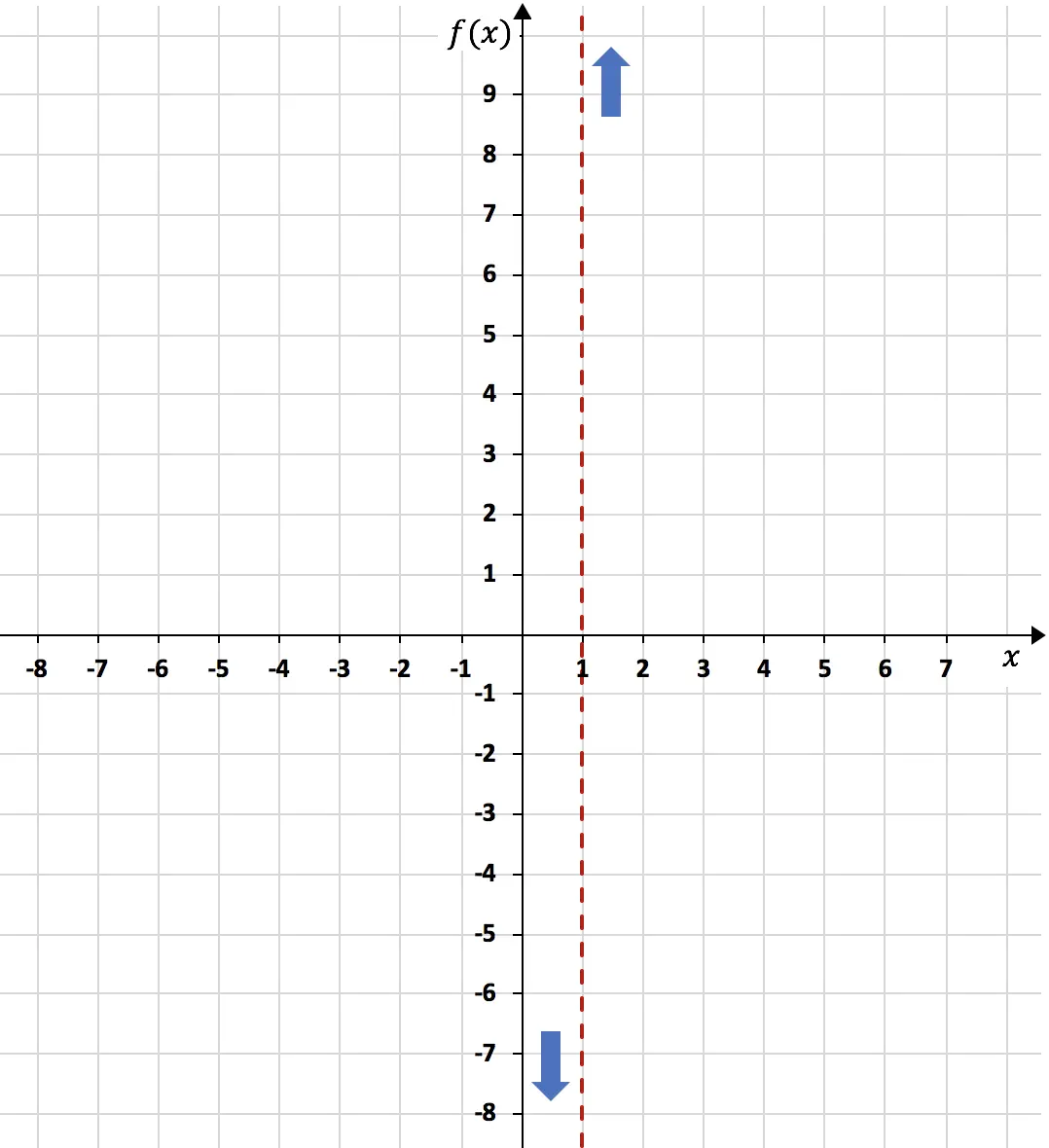
D’altra parte, l’asintoto orizzontale della funzione sarà il risultato del limite infinito della funzione. Ancora:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^2}{x-1} = \cfrac{+\infty}{+\infty } =+\infty$

Ricorda come calcolare i limiti infiniti delle funzioni razionali:

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”> </div> Il limite infinito della funzione ci ha dato +∞, quindi la funzione non ha asintoto orizzontale. Calcoliamo ora l’asintoto obliquo. Gli asintoti obliqui sono della forma <p class=$ $y=mx+n$

. E

$m$

Si calcola con la seguente formula:

$\displaystyle m = \lim_{x \to +\infty} f(x):x$

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2}{x-1}:x$

La x è come se avesse 1 come denominatore:

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2}{x-1}:\cfrac{x}{1}$

È una divisione di frazioni, quindi le moltiplichiamo trasversalmente:

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 \cdot 1 }{(x-1) \cdot x}$

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 }{x^2-x}$

E calcoliamo il limite:

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 }{x^2-x} = \cfrac{+\infty}{+\infty } = \cfrac{1}{1} = 1$

Quindi m=1. Ora calcoliamo

$n$

con la seguente formula:

$\displaystyle n = \lim_{x \to +\infty} \bigl[f(x)-mx\bigr]$

$\displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-1x\right] = \cfrac{+\infty}{+\infty} -(+\infty) = +\infty - \infty$

Ma otteniamo l’indeterminazione infinito meno infinito, quindi dobbiamo ridurre i termini a un denominatore comune. Per fare ciò, moltiplichiamo e dividiamo il termine x per il denominatore della frazione:

$\displaystyle n = \lim_{x \to +\infty}\left[\cfrac{x^2}{x-1}-x\right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x\cdot (x-1)}{x-1} \right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x^2-x}{x-1}\right]$

Ora che i due termini hanno lo stesso denominatore possiamo raggrupparli:

$\displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2-(x^2-x)}{x-1} \right] =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right]$

E infine risolviamo il limite:

$\displaystyle n =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right] = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = 1$

Quindi n = 1. L’asintoto obliquo è quindi:

$y = mx+n$

$y = 1x+1$

$\bm{y = x+1}$

Una volta calcolato l’asintoto obliquo, lo rappresentiamo sullo stesso grafico realizzando una tabella di valori:

$y=x+1$

$\begin{array}{c|c} x & y \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \end{array}$

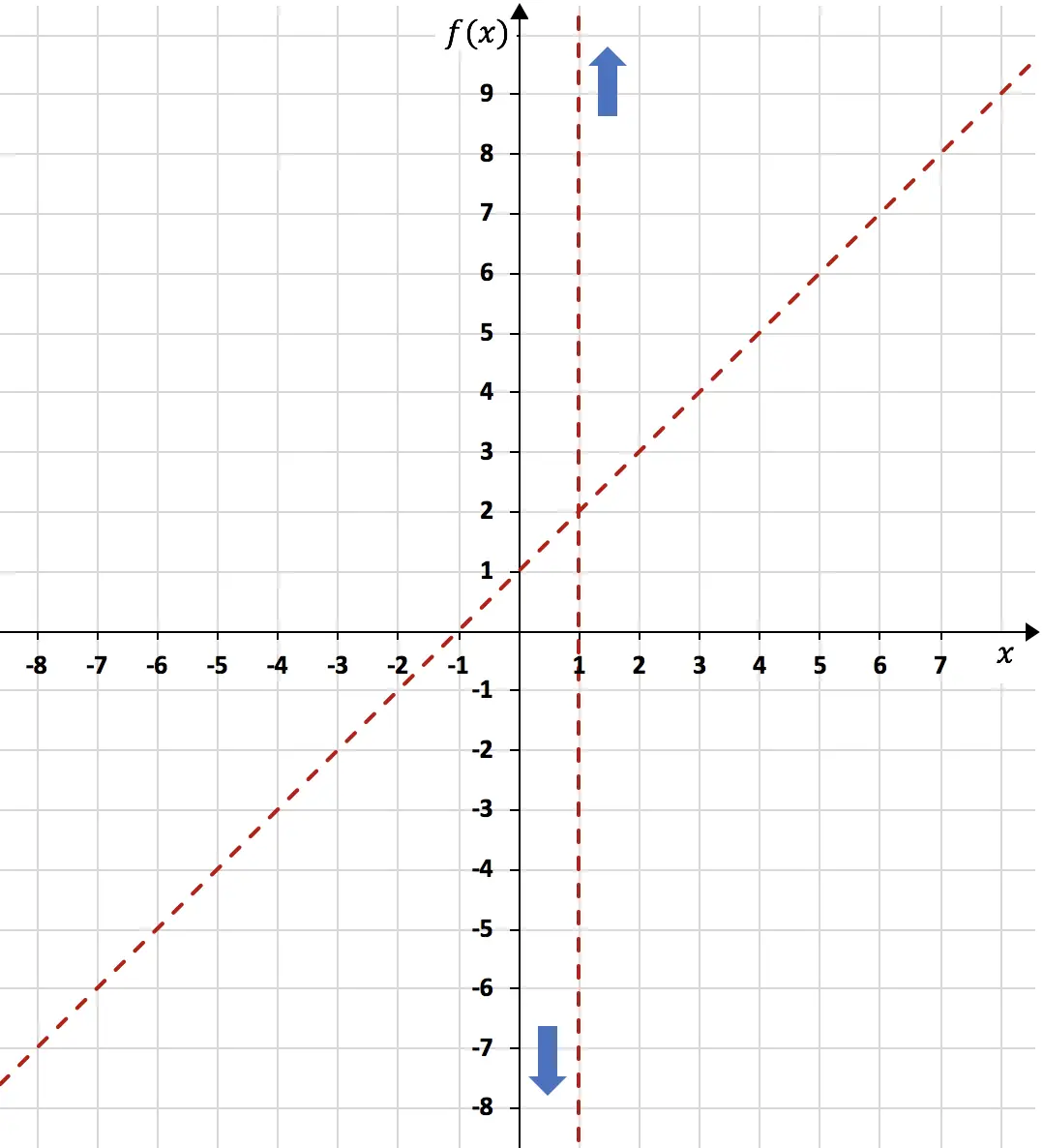
rappresentare funzioni, asintoto obliquo

Ora che conosciamo tutti gli asintoti della funzione, dobbiamo analizzare la monotonicità della funzione . Dobbiamo cioè studiare in quali intervalli la funzione aumenta e in quali intervalli diminuisce. Calcoliamo quindi la derivata prima della funzione:

$f(x)=\cfrac{x^2}{x-1} \ \longrightarrow \ f'(x)= \cfrac{2x\cdot (x-1) - x^2 \cdot 1}{(x-1)^2}$

$f'(x)= \cfrac{2x^2-2x - x^2}{(x-1)^2} = \cfrac{x^2-2x}{(x-1)^2}$

E ora impostiamo la derivata uguale a 0 e risolviamo l’equazione:

$f'(x)=0$

$\cfrac{x^2-2x}{(x-1)^2}=0$

Il termine

$\left(x-1\right)^2}$

Ciò comporta la divisione dell’intero lato sinistro, quindi possiamo moltiplicarlo per l’intero lato destro:

$x^2-2x=0\cdot \left(x-1\right)^2$

$x^2-2x=0$

Estraiamo il fattore comune per risolvere l’equazione quadratica:

$x(x-2)=0$

Perché la moltiplicazione sia uguale a 0, uno dei due elementi della moltiplicazione deve essere zero. Pertanto, impostiamo ciascun fattore uguale a 0 e otteniamo entrambe le soluzioni dell’equazione:

$\displaystyle x\cdot(x-2) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] x-2=0 \ \longrightarrow \ \bm{x= 2} \end{cases}$

Rappresentiamo ora sulla retta numerica tutti i punti critici trovati, cioè i punti che non appartengono al dominio (x=1) e quelli che annullano la derivata (x=0 e x=2):

E valutiamo il segno della derivata in ciascun intervallo, per sapere se la funzione aumenta o diminuisce. Prendiamo quindi un punto in ogni intervallo (mai i punti critici) e guardiamo che segno ha la derivata in quel punto:

$f'(x)=\cfrac{x^2-2x}{\left(x-1\right)^2}$

$f'(-1) = \cfrac{(-1)^2-2(-1)}{\left((-1)-1\right)^2} =\cfrac{+3}{+4} = +0,75 \ \rightarrow \ \bm{+}$

$f'(0,5) = \cfrac{0,5^2-2\cdot 0,5}{\left(0,5-1\right)^2} = \cfrac{-0,75}{+0,25} = -3 \ \rightarrow \ \bm{-}$

$f'(1,5) = \cfrac{1,5^2-2\cdot 1,5}{\left(1,5-1\right)^2} = \cfrac{-0,75}{+0,25} = -3 \ \rightarrow \ \bm{-}$

$f'(3) = \cfrac{3^2-2\cdot 3}{\left(3-1\right)^2} =\cfrac{+3}{+4} = +0,75 \ \rightarrow \ \bm{+}$

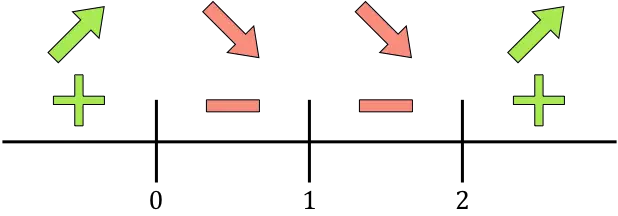
Se la derivata è positiva significa che la funzione è crescente, se la derivata è negativa significa che la funzione è decrescente. Pertanto gli intervalli di crescita e declino sono:

Crescita:

$\bm{(-\infty, 0)\cup (2,+\infty)}$

Diminuire:

$\bm{(0,1)\cup (1,2)}$

Inoltre, per x=0 la funzione passa da crescente a decrescente, quindi x=0 è un massimo relativo della funzione. E in x=2, la funzione passa da decrescente ad crescente, quindi x=2 è un minimo relativo della funzione.

Infine, sostituiamo gli estremi trovati nella funzione originale per trovare la coordinata Y dei punti:

$f(0)=\cfrac{0^2}{0-1} = \cfrac{0}{-1} = 0 \ \longrightarrow \ (0,0)$

$f(2)=\cfrac{2^2}{2-1} = \cfrac{4}{1} = 4 \ \longrightarrow \ (2,4)$

Gli estremi relativi della funzione sono quindi:

Massimo punto

$\bm{(0,0)}$

Minimo da puntare

$\bm{(2,4)}$

Rappresentiamo il massimo e il minimo sul grafico:

rappresentano le funzioni massimo e minimo

Infine è sufficiente studiare la curvatura della funzione , cioè studiare gli intervalli di concavità e convessità della funzione. Per fare ciò calcoliamo la sua derivata seconda:

$f'(x)=\cfrac{x^2-2x}{(x-1)^2} \ \longrightarrow \ f''(x)= \cfrac{(2x-2)\cdot (x-1)^2- (x^2-2x)\cdot 2(x-1)\cdot 1}{\left(\left(x-1\right)^2\right)^2}$

$f''(x)= \cfrac{(2x-2)\cdot (x-1)^2- (x^2-2x)\cdot 2(x-1)}{(x-1)^4}$

$f''(x)= \cfrac{(2x-2)\cdot (x-1)^{\cancel{2}}- (x^2-2x)\cdot 2\cancel{(x-1)}}{(x-1)^{\cancelto{3}{4}}} = \cfrac{(2x-2)\cdot (x-1)- (x^2-2x)\cdot 2}{(x-1)^3}$

$f''(x)= \cfrac{2x^2-2x-2x+2- (2x^2-4x)}{(x-1)^3} =\cfrac{2x^2-2x-2x+2- 2x^2+4x}{(x-1)^3}$

$f''(x) =\cfrac{2}{(x-1)^3}$

E ora impostiamo la derivata seconda uguale a zero e risolviamo l’equazione:

$f''(x)=0$

$\cfrac{2}{(x-1)^3} =0$

$2=0\cdot \left(x-1\right)^3$

$2=0$

2 non sarà mai uguale a 0, quindi l’equazione

$f''(x)=0$

Non c’è soluzione.

Rappresentiamo ora sulla retta numerica tutti i punti critici trovati, cioè i punti che non appartengono al dominio (x=1) e quelli che annullano la derivata seconda (in questo caso non ce ne sono has):

E valutiamo il segno della derivata in ogni intervallo, per sapere se la funzione è convessa o concava. Prendiamo quindi un punto in ogni intervallo (mai i punti singolari) e guardiamo che segno ha la derivata in questo punto:

$f''(x) =\cfrac{2}{(x-1)^3}$

$f''(0) =\cfrac{2}{(0-1)^3} = \cfrac{2}{-1}=-2 \ \rightarrow \ \bm{-}$

$f''(2) =\cfrac{2}{(2-1)^3} = \cfrac{2}{1}=2 \ \rightarrow \ \bm{+}$

E infine deduciamo gli intervalli di concavità e convessità della funzione. Se la derivata seconda è positiva significa che la funzione è convessa.

$(\bm{\cup})$

, e se la derivata seconda è negativa significa che la funzione è concava

$(\bm{\cap})$

. Gli intervalli di concavità e convessità sono quindi:

Convesso

$(\bm{\cup})$

$\bm{(1,+\infty)}$

Concavo

$(\bm{\cap})$

$\bm{(-\infty,1)}$

Tuttavia, anche se c’è un cambiamento nella curvatura in x=1, non è un punto di flesso. Perché x=1 non appartiene al dominio della funzione.

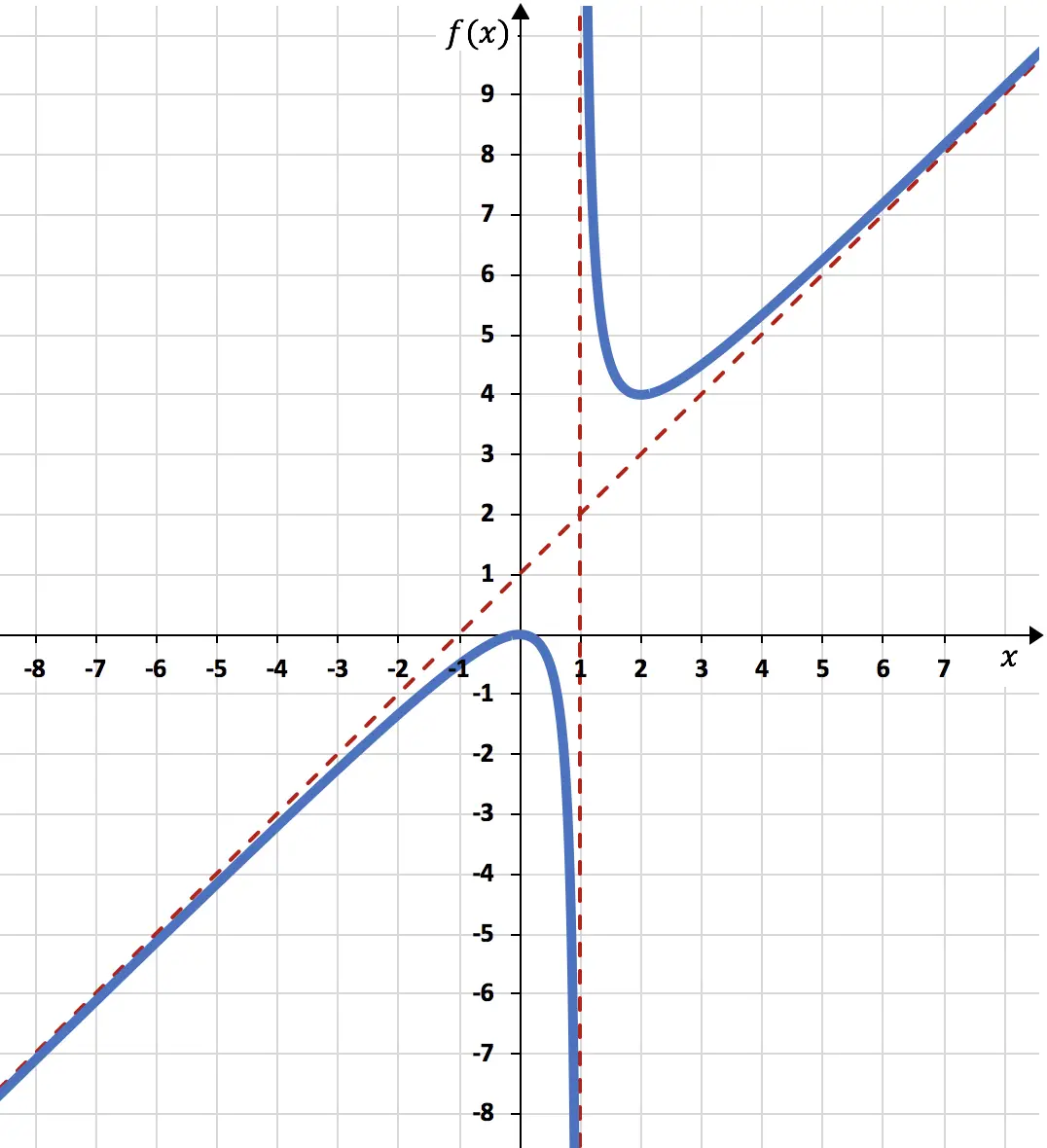
Quindi possiamo finire di rappresentare la funzione utilizzando tutto ciò che abbiamo calcolato:

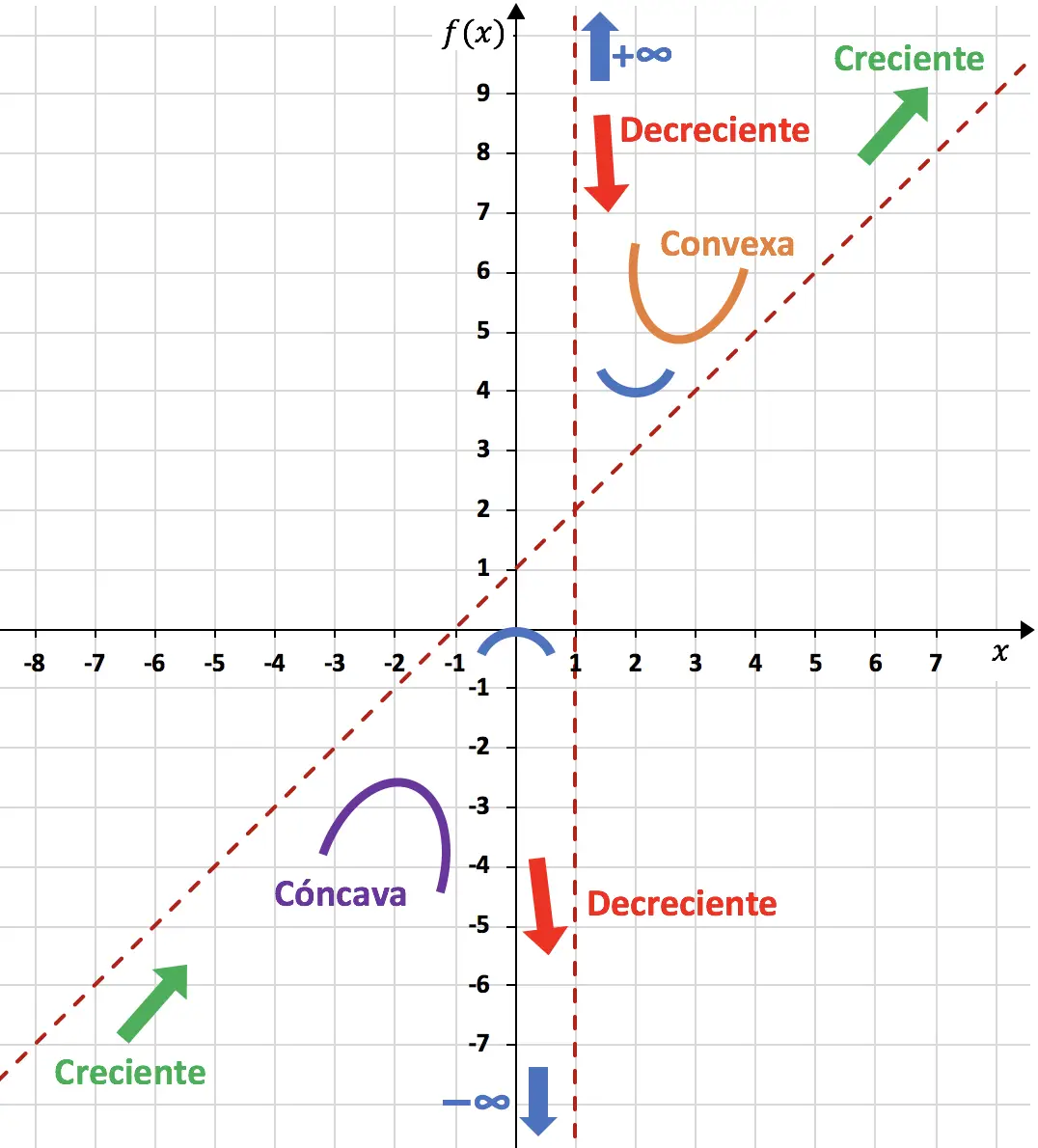
La funzione rappresentata nel grafico si presenta quindi così:

rappresentazione grafica della funzione razionale

Esercizi risolti per rappresentare le funzioni

Esercizio 1

Rappresentare graficamente la seguente funzione polinomiale:

$\displaystyle f(x)=x^3-3x^2+4$

Vedi la soluzione

La prima cosa da fare è calcolare il dominio di definizione della funzione. Questa è una funzione polinomiale, quindi il dominio è costituito solo da numeri reali:

$\text{Dom } f= \mathbb{R}$

Per trovare il punto di intersezione con l’asse X, risolviamo

$f(x)= 0.$

$f(x)=0$

$x^3-3x^2+4=0$

Questa è un’equazione di grado maggiore di 2. Pertanto, fattorizziamo l’equazione:

$(x+1)(x^2-4x+4)=0$

Quindi x=-1 è una soluzione. E calcoliamo le altre soluzioni risolvendo l’equazione quadratica risultante:

$\begin{aligned}x & =\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} =\cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1 \cdot 4}}{2\cdot 1} \\[2ex] &=\cfrac{+4 \pm \sqrt{16-16}}{2} =\cfrac{4 \pm \sqrt{0}}{2} = \cfrac{4 }{2 } = 2\end{aligned}$

I punti di intersezione con l’asse X sono quindi:

$\bm{(-1,0)}$

$\bm{(2,0)}$

E per trovare il punto di intersezione con l’asse Y, calcoliamo

$f(0).$

Poiché x è sempre 0 sull’asse Y:

$f(0)=0^3-3\cdot0^2+4 = 4$

Il punto di intersezione con l’asse Y è quindi:

$\bm{(0,4)}$

Per vedere se la funzione ha asintoti verticali, dobbiamo calcolare il limite della funzione nei punti che non appartengono al dominio. In questo caso il dominio comprende tutti i numeri reali. La funzione quindi non ha asintoto verticale.

D’altra parte, l’asintoto orizzontale della funzione sarà il risultato del limite infinito della funzione. Ancora:

$\displaystyle \lim_{x \to +\infty} \ x^3-3x^2+4 =(+\infty)^3 = +\infty$

Il limite infinito della funzione ci ha dato +∞, quindi la funzione non ha asintoto orizzontale.

Calcoliamo ora l’asintoto obliquo. Gli asintoti obliqui sono della forma

$y=mx+n.$

$m$

Si calcola con la seguente formula:

$\displaystyle m = \lim_{x \to +\infty} f(x):x = \lim_{x \to +\infty} \left( x^3-3x^2+4\right): x =$

$\displaystyle = \lim_{x \to +\infty} \cfrac{x^3-3x^2+4}{x} = \cfrac{+\infty}{+\infty} = +\infty$

Il limite ci ha dato +∞, quindi anche la funzione non ha asintoto obliquo.

Per studiare la monotonicità della funzione, dobbiamo prima calcolare la sua derivata:

$f(x)= x^3-3x^2+4 \ \longrightarrow \ f'(x)= 3x^2-6x$

Ora impostiamo la derivata uguale a 0 e risolviamo l’equazione:

$f'(x)= 0$

$3x^2-6x=0$

$x(3x-6)=0$

$\displaystyle x\cdot(3x-6) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] 3x-6=0 \ \longrightarrow \ x= \cfrac{6}{3} = 2 \end{cases}$

Rappresentiamo ora sulla retta numerica tutti i punti singolari ottenuti, cioè i punti che non appartengono al dominio (in questo caso lo appartengono tutti) e quelli che annullano la derivata (x=0 e x=2) :

E valutiamo il segno della derivata in ciascun intervallo, per sapere se la funzione aumenta o diminuisce. Prendiamo quindi un punto in ogni intervallo (mai i punti singolari) e guardiamo che segno ha la derivata in questo punto:

$f'(-1)=3(-1)^2-6(-1)= 3+6 = 9\ \rightarrow \ \bm{+}$

$f'(1)=3\cdot 1^2-6\cdot 1= 3-6 = -3\ \rightarrow \ \bm{-}$

$f'(3)=3\cdot 3^2-6\cdot 3= 27-18 = 9\ \rightarrow \ \bm{+}$

Se la derivata è positiva significa che la funzione è crescente, se la derivata è negativa significa che la funzione è decrescente. Pertanto gli intervalli di crescita e declino sono:

Crescita:

$\bm{(-\infty,0)\cup (2,+\infty)}$

Diminuire:

$\bm{(0,2)}$

La funzione passa da crescente a decrescente in x=0, quindi x=0 è il massimo della funzione. E la funzione passa da decrescente ad crescente in x=2, quindi x=2 è il minimo della funzione.

Infine, sostituiamo gli estremi trovati nella funzione originale per trovare le coordinate Y dei punti:

$f(0)=0^3-3\cdot 0^2+4 = 4 \ \longrightarrow \ (0,4)$

$f(2)=2^3-3\cdot 2^2+4 = 8-3 \cdot 4 +4 = 0 \ \longrightarrow \ (2,0)$

Gli estremi relativi della funzione sono quindi:

Massimo punto

$\bm{(0,4)}$

Minimo da puntare

$\bm{(2,0)}$

Per studiare la curvatura della funzione, calcoliamo la sua derivata seconda:

$f'(x)= 3x^2-6x \ \longrightarrow \ f''(x)= 6x-6$

Ora impostiamo la derivata seconda uguale a 0 e risolviamo l’equazione:

$f''(x)= 0$

$6x-6=0$

$6x=6$

$x= \cfrac{6}{6} = 1$

Rappresentiamo sulla retta tutti i punti singolari trovati, cioè i punti che non appartengono al dominio (in questo caso lo appartengono tutti) e quelli che annullano la derivata (x=1):

E ora valutiamo il segno della derivata seconda in ogni intervallo, per sapere se la funzione è concava o convessa. Prendiamo quindi un punto in ogni intervallo (mai i punti singolari) e guardiamo che segno ha la derivata seconda in questo punto:

$f''(0)=6\cdot 0-6= -6 \ \rightarrow \ \bm{-}$

$f''(2)=6\cdot 2-6= 12-6= 6 \ \rightarrow \ \bm{+}$

Se la derivata seconda è positiva significa che la funzione è convessa.

$(\bm{\cup})$

, e se la derivata seconda è negativa significa che la funzione è concava

$(\bm{\cap})$

. Gli intervalli di concavità e convessità sono quindi:

Convesso

$(\bm{\cup})$

$\bm{(1,+\infty)}$

Concavo

$(\bm{\cap})$

$\bm{(-\infty,1)}$

Inoltre, la funzione cambia da concava a convessa in x=1, quindi x=1 è un punto di flesso della funzione.

Infine, sostituiamo i punti di flesso trovati nella funzione originale per trovare la coordinata Y dei punti:

$f(1)=1^3-3\cdot 1^2+ 4= 1 -3 +4 =2 \ \longrightarrow \ (1,2)$

I punti di svolta della funzione sono quindi:

Punti di svolta:

$\bm{(1,2)}$

Infine, sulla base di tutte le informazioni che abbiamo calcolato, rappresentiamo graficamente la funzione:

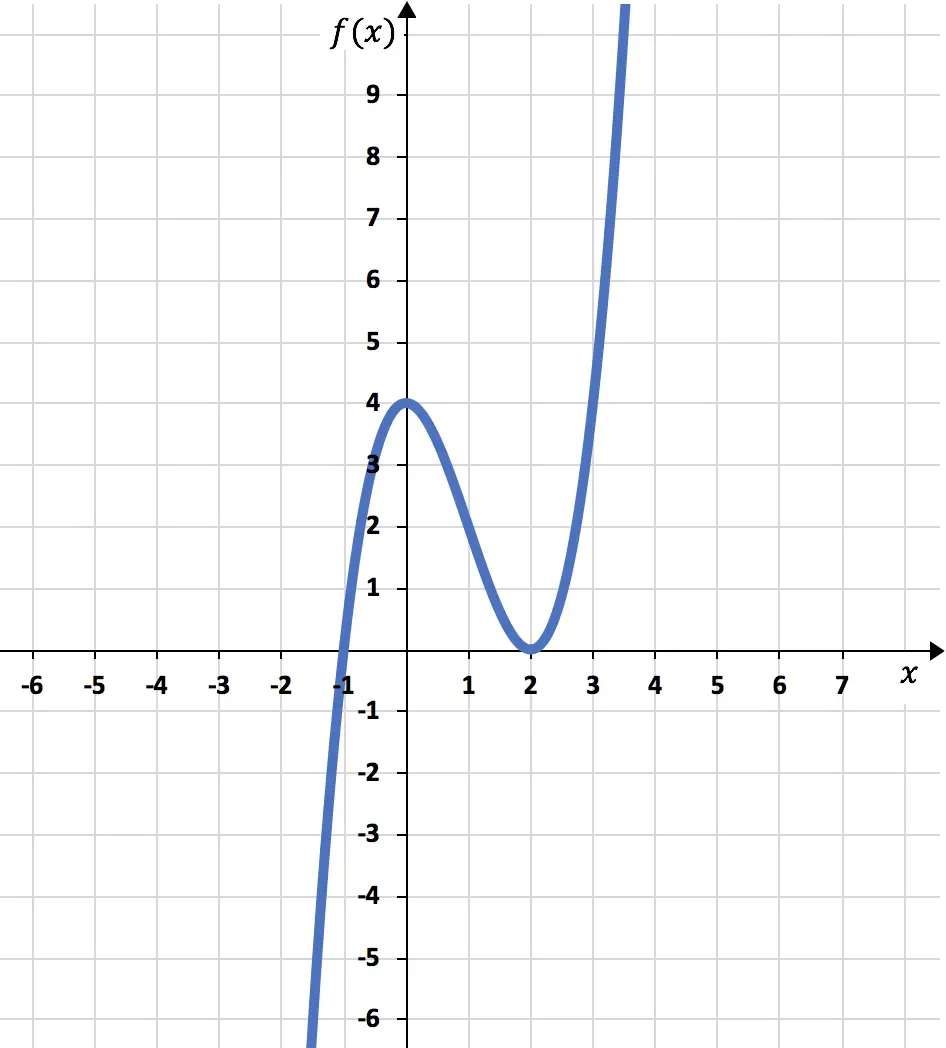
rappresentazione grafica della funzione polinomiale

Esercizio 2

Rappresentare graficamente la seguente funzione razionale:

$\displaystyle f(x)=\frac{x^2+2}{x^2-1}$

Vedi la soluzione

Per trovare il dominio della funzione, impostiamo il denominatore uguale. porta la frazione a zero e risolvi l’equazione risultante:

$x^2-1= 0$

$x^2=1$

$\sqrt{x^2}=\sqrt{1}$

$x=\pm 1$

$\text{Dom } f= \mathbb{R}-\{-1, +1 \}$

In secondo luogo, determiniamo le soglie della funzione con l’asse x uguale all’espressione algebrica della funzione. acciaio:

$f(x)=0$

$\cfrac{x^2+2}{x^2-1}=0$

$x^2+2=0\cdot (x^2-1)$

$x^2+2=0$

$x^2=-2$

$x=\sqrt{-2} \quad \color{red}\bm{\times}$

Non esiste la radice quadrata di un numero negativo. Pertanto, la funzione non interseca l’asse X.

E per trovare il punto di intersezione con l’asse del computer, valutiamo la funzione in x=0.

$f(0)=\cfrac{0^2+2}{0^2-1}= \cfrac{2}{-1} = -2$

Il punto di intersezione con l’asse Y è quindi:

$\bm{(0,-2)}$

Per vedere se la funzione ha asintoti verticali, dobbiamo calcolare il limite della funzione nei punti che non appartengono al dominio (in questo caso x=-1 e x=+1). E se il risultato è infinito, è un asintoto verticale. Ancora:

$\displaystyle \lim_{x \to -1} \cfrac{x^2+2}{x^2-1} = \cfrac{(-1)^2+2}{(-1)^2-1} =\cfrac{1+2}{1-1}= \cfrac{3}{0} = \infty$

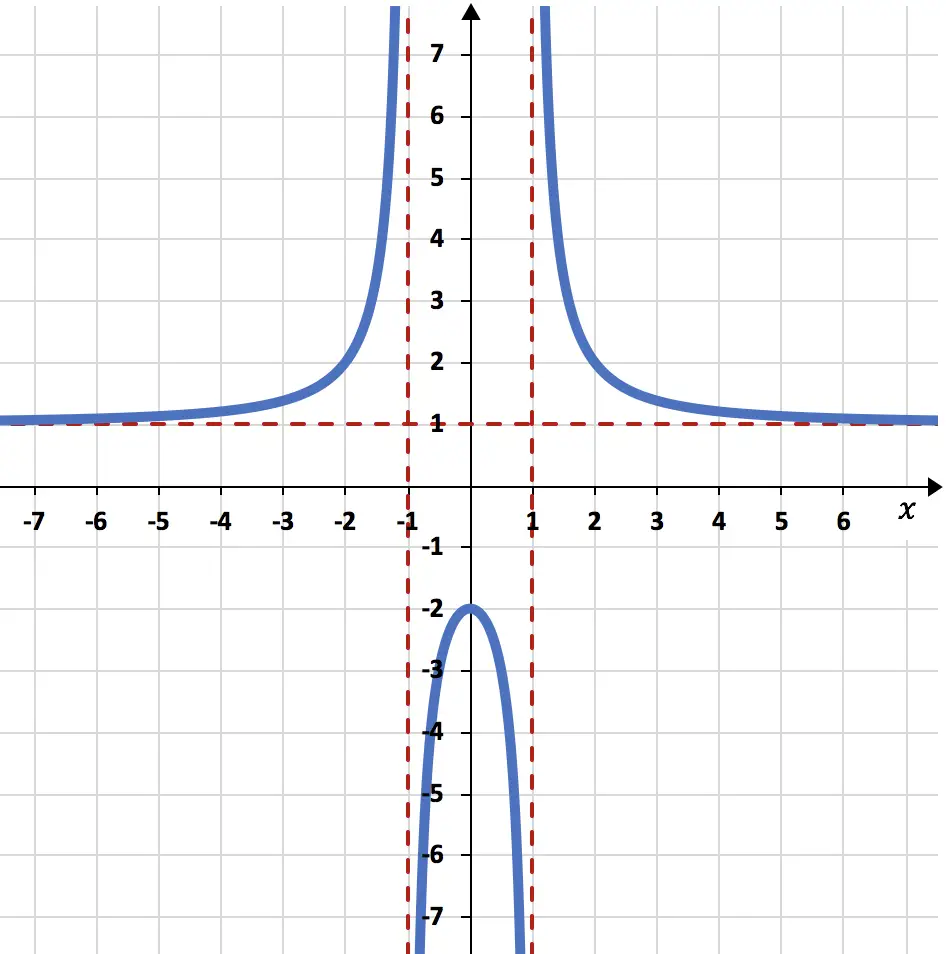
Poiché il limite della funzione quando x si avvicina a -1 dà infinito, x=-1 è un asintoto verticale.

Calcoliamo i limiti laterali dell’asintoto x=-1 sostituendo nella funzione un numero molto vicino ad esso:

$\displaystyle f(-1,1)=\cfrac{(-1,1)^2+2}{(-1,1)^2-1} =+15,29 \longrightarrow \lim_{x \to -1^{-}} \ \cfrac{x^2+2}{x^2-1} = +\infty$

$\displaystyle f(-0,9)=\cfrac{(-0,9)^2+2}{(-0,9)^2-1} =-14,79 \longrightarrow \lim_{x \to -1^{+}} \ \cfrac{x^2+2}{x^2-1} = -\infty$

Ora vediamo se x=+1 è un asintoto verticale:

$\displaystyle \lim_{x \to +1} \cfrac{x^2+2}{x^2-1} = \cfrac{1^2+2}{1^2-1} =\cfrac{1+2}{1-1}= \cfrac{3}{0} = \infty$

Poiché il limite della funzione quando x si avvicina a +1 dà infinito, x=+1 è un asintoto verticale.

Calcoliamo i limiti laterali dell’asintoto x=1 sostituendo nella funzione un numero molto vicino ad esso:

$\displaystyle f(0,9)=\cfrac{(0,9)^2+2}{(0,9)^2-1} =-14,79 \longrightarrow \lim_{x \to +1^{-}} \ \cfrac{x^2+2}{x^2-1} = -\infty$

$\displaystyle f(1,1)=\cfrac{(1,1)^2+2}{(1,1)^2-1} =+15,29 \longrightarrow \lim_{x \to +1^{+}} \ \cfrac{x^2+2}{x^2-1} = +\infty$

D’altra parte, l’asintoto orizzontale della funzione sarà il risultato del limite infinito della funzione. Ancora:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^2+2}{x^2-1} = \cfrac{+\infty}{+\infty } =\cfrac{1}{1} = 1$

Il limite infinito della funzione ci ha dato 1, quindi la funzione ha un asintoto orizzontale in y=1.

Poiché la funzione ha un asintoto orizzontale, non avrà un asintoto obliquo.

Differenziamo la funzione quindi studiamo gli intervalli di crescita e diminuzione:

$f(x)=\cfrac{x^2+2}{x^2-1} \ \longrightarrow \ f'(x)= \cfrac{2x \cdot (x^2-1) -(x^2+2) \cdot 2x}{\left(x^2-1 \right)^2}$

$f'(x)= \cfrac{2x^3-2x - (2x^3+4x) }{\left(x^2-1 \right)^2} = \cfrac{-6x}{\left(x^2-1 \right)^2}$

Ora impostiamo la derivata uguale a 0 e risolviamo l’equazione:

$f'(x)= 0$

$\cfrac{-6x}{\left(x^2-1 \right)^2}=0$

$-6x=0\cdot\left(x^2-1 \right)^2$

$-6x= 0$

$x=\cfrac{0}{-6} = 0$

Rappresentiamo sulla retta tutti i punti critici calcolati, ovvero i punti che non appartengono al dominio (x=-1 e x=+1) e quelli che annullano la derivata (x=0):

$f'(-2)= \cfrac{-6(-2)}{\left((-2)^2-1 \right)^2} = \cfrac{12}{9} =1,33 \ \rightarrow \ \bm{+}$

$f'(-0,5)= \cfrac{-6(-0,5)}{\left((-0,5)^2-1 \right)^2} = \cfrac{3}{0,56} =5,33 \ \rightarrow \ \bm{+}$

$f'(0,5)= \cfrac{-6\cdot 0,5}{\left(0,5^2-1 \right)^2} = \cfrac{-3}{0,56} =-5,33 \ \rightarrow \ \bm{-}$

$f'(2)= \cfrac{-6\cdot 2}{\left(2^2-1 \right)^2} = \cfrac{-12}{9} =-1,33 \ \rightarrow \ \bm{-}$

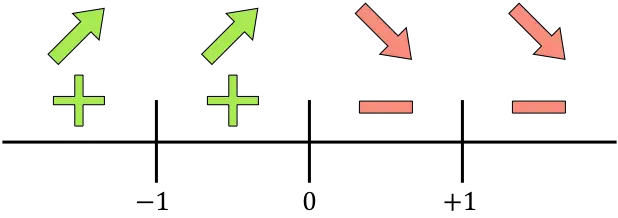
La funzione aumenta dove la derivata è positiva e diminuisce dove la funzione è negativa:

Crescita:

$\bm{(-\infty,-1)\cup (-1,0)}$

Diminuire:

$\bm{(0,1)\cup (1,+\infty)}$

La funzione passa da crescente a decrescente in x=0, quindi x=0 è un massimo locale della funzione.

Sostituiamo l’estremo trovato nella funzione originale per trovare la coordinata Y del punto:

$f(0)=\cfrac{0^2+2}{0^2-1}= \cfrac{2}{-1} = -2 \ \longrightarrow \ (0,-2)$

Gli estremi relativi della funzione sono quindi:

Massimo punto

$\bm{(0,-2)}$

Per studiare la curvatura della funzione, calcoliamo la sua derivata seconda:

$f'(x)=\cfrac{-6x}{\left(x^2-1 \right)^2} \ \longrightarrow <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-273969cf60ee8cf3413ee2f8b1db7688_l3.png" height="129" width="476" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f''(x)= \cfrac{-6 \cdot \left(x^2-1 \right)^2 - (-6x) \cdot 2(x^2-1) \cdot 2x}{ \left(\left(x^2-1 \right)^2\right)^2}$$ f''(x)= \cfrac{-6 \left(x^2-1 \right)^2 -(-6x)\cdot 4x(x^2-1)}{\left(x^2 -1\right)^4} =\]" title="Rendered by QuickLaTeX.com"/> \cfrac{-6 \left(x^2-1 \right)^2 + 24x^2(x^2-1)}{\left(x^2 -1\right)^4}” title=”Rendered by QuickLaTeX.com”> <p class=$ Tutti i termini hanno

$(x^2-1)$

, possiamo quindi semplificare la frazione:

$f''(x)= \cfrac{-6 \left(x^2-1 \right)^{\cancel{2}} + 24x^2\cancel{(x^2-1)}}{\left(x^2-1 \right)^\cancelto{3}{4}} =\cfrac{-6 \left(x^2-1 \right) + 24x^2}{\left(x^2 -1\right)^3}$

$f''(x)= \cfrac{-6x^2+6 + 24x^2}{\left(x^2 -1\right)^3} =\cfrac{18x^2+6}{\left(x^2 -1\right)^3}$

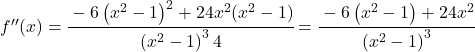
Ora impostiamo la derivata seconda uguale a 0 e risolviamo l’equazione:

$f''(x)= 0$

$\cfrac{18x^2+6}{\left(x^2 -1\right)^3}=0$

$18x^2+6=0\cdot \left(x^2 -1\right)^3$

$18x^2+6= 0$

$18x^2=-6$

$x^2=\cfrac{-6}{18}$

$x^2=-0,33$

$x=\sqrt{-0,33} \quad \color{red}\bm{\times}$

Non esiste la radice quadrata di un numero negativo. Quindi non ha senso che corrisponda

$f''(x)=0$

Rappresentiamo ora sulla retta tutti i punti singolari trovati, cioè i punti che non appartengono al dominio (x=-1 e x=+1) e quelli che annullano la derivata seconda (in questo caso non ci sono Qualunque):

E valutiamo il segno della derivata seconda in ogni intervallo, per sapere se la funzione è concava o convessa. Prendiamo quindi un punto in ogni intervallo (mai i punti singolari) e guardiamo che segno ha la derivata seconda in questo punto:

$f''(-2)=\cfrac{18(-2)^2+6}{\left((-2)^2 -1\right)^3}= \cfrac{78}{27} = 2,89 \ \rightarrow \ \bm{+}$

$f''(0)=\cfrac{18\cdot 0^2+6}{\left(0^2 -1\right)^3}= \cfrac{6}{-1} = -6 \ \rightarrow \ \bm{-}$

$f''(2)=\cfrac{18\cdot 2^2+6}{\left(2^2 -1\right)^3}= \cfrac{78}{27} = 2,89 \ \rightarrow \ \bm{+}$

Se la derivata seconda è positiva significa che la funzione è convessa.

$(\bm{\cup})$

, e se la derivata seconda è negativa significa che la funzione è concava

$(\bm{\cap})$

. Gli intervalli di concavità e convessità sono quindi:

Convesso

$(\bm{\cup})$

$\bm{(-\infty, -1) \cup (1, +\infty)}$

Concavo

$(\bm{\cap})$

$\bm{(-1,1)}$

Tuttavia, sebbene vi sia un cambiamento nella curvatura in x=-1 e in x=1, questi non sono punti di flesso. Perché non appartengono al dominio della funzione.

E infine, rappresentiamo graficamente la funzione utilizzando tutti i calcoli eseguiti:

esercizio sulle funzioni grafiche risolto

Esercizio 3

Traccia su un grafico la seguente funzione razionale:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Vedi la soluzione

Questa è una funzione razionale, quindi dobbiamo impostare il denominatore uguale a 0 per vedere quali numeri non appartengono al dominio della funzione:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

Per trovare il punto di intersezione con l’asse X, risolviamo

$f(x)= 0.$

Poiché la funzione ha sempre un valore pari a 0 sull’asse X:

$f(x)=0$

$\cfrac{x^3}{x^2-4}=0$

$x^3=0\cdot (x^2-4)$

$x^3=0$

$x=\sqrt[3]{0}=0$

Il punto di intersezione con l’asse X è quindi:

$\bm{(0,0)}$

E per trovare il punto di intersezione con l’asse Y, calcoliamo

$f(0).$

Poiché x è sempre 0 sull’asse Y:

$f(0)=\cfrac{0^3}{0^2-4} = \cfrac{0}{-4} = 0$

Il punto di intersezione con l’asse Y è quindi:

$\bm{(0,0)}$

In questo caso il punto di intersezione con l’asse X coincide con il punto di intersezione con l’asse Y, poiché la funzione passa per l’origine delle coordinate.

Per vedere se la funzione ha asintoti verticali, dobbiamo calcolare il limite della funzione nei punti che non appartengono al dominio (in questo caso x=-2 e x=+2). E se il risultato è infinito, è un asintoto verticale. Ancora:

$\displaystyle \lim_{x \to -2} \cfrac{x^3}{x^2-4} = \cfrac{(-2)^3}{(-2)^2-4} =\cfrac{-8}{4-4}= \cfrac{-8}{0} = \infty$

Poiché il limite della funzione quando x si avvicina a -2 dà infinito, x=-2 è un asintoto verticale.

Calcoliamo i limiti laterali dell’asintoto x=-2 sostituendo nella funzione un numero molto vicino ad esso:

$\displaystyle f(-2,1)=\cfrac{(-2,1)^3}{(-2,1)^2-4} =-22,59 \longrightarrow \lim_{x \to -2^{-}} \cfrac{x^3}{x^2-4} = -\infty$

$\displaystyle f(-1,9)=\cfrac{(-1,9)^3}{(-1,9)^2-4} =+17,59 \longrightarrow \lim_{x \to -2^{+}} \cfrac{x^3}{x^2-4} = +\infty$

Ora vediamo se x=+2 è un asintoto verticale:

$\displaystyle \lim_{x \to +2} \cfrac{x^3}{x^2-4} = \cfrac{(2)^3}{(2)^2-4} =\cfrac{8}{4-4}= \cfrac{8}{0} = \infty$

Poiché il limite della funzione quando x si avvicina a +2 dà infinito, x=+2 è un asintoto verticale.

Calcoliamo i limiti laterali dell’asintoto x=2 sostituendo nella funzione un numero molto vicino ad esso:

$\displaystyle f(1,9)=\cfrac{1,9^3}{1,9^2-4} =-17,59 \longrightarrow \lim_{x \to 2^{-}} \cfrac{x^3}{x^2-4} = -\infty$

$\displaystyle f(2,1)=\cfrac{2,1^3}{2,1^2-4} =22,59 \longrightarrow \lim_{x \to 2^{+}} \cfrac{x^3}{x^2-4} = +\infty$

D’altra parte, l’asintoto orizzontale della funzione sarà il risultato del limite infinito della funzione. Ancora:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^3}{x^2-4} = \cfrac{+\infty}{+\infty } =+\infty$

Il limite infinito della funzione ci ha dato +∞, quindi la funzione non ha asintoto orizzontale.

Calcoliamo ora l’asintoto obliquo. Gli asintoti obliqui sono della forma

$y=mx+n.$

$m$

Si calcola con la seguente formula:

$\displaystyle m = \lim_{x \to +\infty} f(x):x = \lim_{x \to +\infty} \cfrac{x^3}{x^2-4}: x =\lim_{x \to +\infty} \cfrac{x^3}{x^2-4}: \frac{x}{1}$

$\displaystyle m =\lim_{x \to +\infty}\cfrac{x^3\cdot 1}{(x^2-4)\cdot x} =\lim_{x \to +\infty}\cfrac{x^3}{x^3-4x}$

$\displaystyle m =\lim_{x \to +\infty}\cfrac{x^3}{x^3-4x} = \frac{+\infty}{+\infty} = \frac{1}{1} = \bm{1}$

Una volta conosciuta la pendenza dell’asintoto obliquo, determiniamo l’intercetta utilizzando la seguente formula:

$\displaystyle n = \lim_{x \to +\infty} \left[f(x)-mx\right] = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-1x\right]$

$\displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}$

Ma otteniamo l’indeterminazione ∞ – ∞. È quindi necessario ridurre i termini ad un denominatore comune. Per fare ciò, moltiplichiamo e dividiamo la x per il denominatore della frazione:

$\displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x \cdot (x^2-4)}{(x^2-4)}\right] =\lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x^3-4x}{x^2-4}\right]$

$\displaystyle n = \lim_{x \to +\infty} \cfrac{x^3- (x^3-4x)}{x^2-4} = \lim_{x \to +\infty} \cfrac{4x}{x^2-4}$

$\displaystyle n =\lim_{x \to +\infty} \cfrac{4x}{x^2-4} = \cfrac{+\infty}{\infty} =\bm{0}$

In breve, l’asintoto obliquo è:

$y = mx+n$

$y = 1x + 0$

$\bm{y = x }$

Per studiare la monotonicità della funzione, dobbiamo prima calcolare la sua derivata:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

Ora impostiamo la derivata uguale a 0 e risolviamo l’equazione:

$f'(x)= 0$

$\cfrac{x^4-12x^2}{\left(x^2-4\right)^2}=0$

$x^4-12x^2=0\cdot \left(x^2-4\right)^2$

$x^4-12x^2=0$

$x^2(x^2-12)=0$

$\displaystyle x^2\cdot(x^2-12) =0 \longrightarrow \begin{cases} x^2 =0 \ \longrightarrow \ \bm{x=0} \\[2ex] x^2-12=0 \ \longrightarrow \ x=\sqrt{12} \ \longrightarrow \ \bm{x= \pm 3,46} \end{cases}$

Rappresentiamo ora sulla retta tutti i punti singolari trovati, cioè i punti che non appartengono al dominio (x=-2 e x=+2) e quelli che annullano la derivata (x=0, x=- 3,46 e x= +3,46):

$f'(-4)= \cfrac{(-4)^4-12(-4)^2}{\left((-4)^2-4\right)^2} = \cfrac{64}{144} = 0,44 \ \rightarrow \ \bm{+}$

$f'(-3)= \cfrac{(-3)^4-12(-3)^2}{\left((-3)^2-4\right)^2} = \cfrac{-27}{25} = -1,08 \ \rightarrow \ \bm{-}$

$f'(-1)= \cfrac{(-1)^4-12(-1)^2}{\left((-1)^2-4\right)^2} = \cfrac{-11}{9} = -1,22 \ \rightarrow \ \bm{-}$

$f'(1)= \cfrac{1^4-12\cdot1^2}{\left(1^2-4\right)^2} = \cfrac{-11}{9} = -1,22 \ \rightarrow \ \bm{-}$

$f'(3)= \cfrac{3^4-12\cdot 3^2}{\left(3^2-4\right)^2} = \cfrac{-27}{25} = -1,08 \ \rightarrow \ \bm{-}$

$f'(4)= \cfrac{4^4-12\cdot 4^2}{\left(4^2-4\right)^2} = \cfrac{64}{144} = 0,44 \ \rightarrow \ \bm{+}$

Se la derivata è positiva significa che la funzione è crescente, se la derivata è negativa significa che la funzione è decrescente. Pertanto gli intervalli di crescita e declino sono:

Crescita:

$\bm{(-\infty,-3,46)\cup (3,46,+\infty)}$

Diminuire:

$\bm{(-3,46,-2)\cup(-2,0)\cup (0,2) \cup (2,3,46)}$

La funzione passa da crescente a decrescente in x=-3,46, quindi x=-3,46 è il massimo della funzione. E la funzione passa da decrescente ad crescente in x=3,46, quindi x=3,46 è il minimo della funzione.

Determiniamo le coordinate Y dei relativi estremi:

$f(-3,46)=\cfrac{(-3,46)^3}{(-3,46)^2-4} = \cfrac{-41,42}{7,97}=-5,20 \ \longrightarrow \ (-3,46,-5,20)$

$f(3,46)=\cfrac{3,46^3}{3,46^2-4} = \cfrac{41,42}{7,97}=5,20 \ \longrightarrow \ (3,46,5,20)$

Gli estremi relativi della funzione sono quindi:

Massimo punto

$\bm{(-3,46,-5,20)}$

Minimo da puntare

$\bm{(3,46,5,20)}$

Per studiare la curvatura della funzione, calcoliamo la derivata seconda della funzione:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Ora impostiamo la derivata seconda uguale a 0 e risolviamo l’equazione:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

$x(8x^2+96)=0$

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

Non esiste una soluzione poiché non esiste una radice negativa di un numero reale.

Rappresentiamo ora sulla retta tutti i punti singolari trovati, cioè i punti che non appartengono al dominio (x=-2 e x=+2) e quelli che annullano la derivata seconda (x=0):

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot 1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

Se la derivata seconda è positiva significa che la funzione è convessa.

$(\bm{\cup})$

, e se la derivata seconda è negativa significa che la funzione è concava

$(\bm{\cap})$

. Gli intervalli di concavità e convessità sono quindi:

Convesso

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

Concavo

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

Tuttavia, sebbene vi sia un cambiamento nella curvatura in x=-2 ex=+2, questi non sono punti di flesso. Perché x=-2 e x=+2 non appartengono al dominio della funzione. Invece in x=0 si verifica un cambiamento di curvatura (la funzione passa da convessa a concava) e questo appartiene alla funzione, quindi x=0 è un punto di flesso.

Sostituiamo i punti di flesso trovati nella funzione originale per trovare l’altra coordinata del punto di flesso:

$f(0) = \cfrac{0^3}{0^2-4} = \cfrac{0}{-4} =0\ \longrightarrow \ (0,0)$

I punti di svolta della funzione sono quindi:

Punti di svolta:

$\bm{(0,0)}$

Infine, sulla base di tutte le informazioni che abbiamo calcolato, rappresentiamo la funzione:

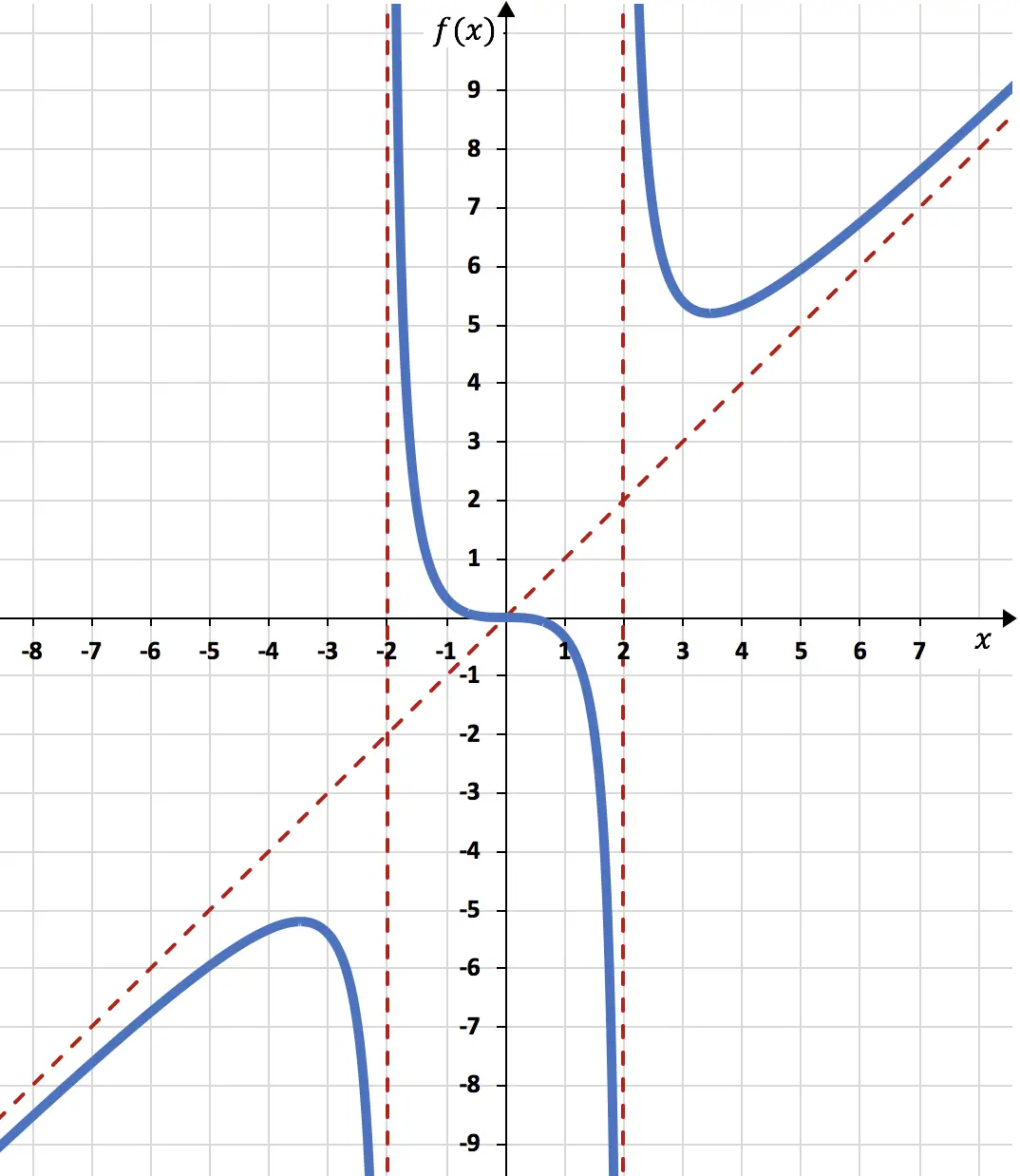
rappresentazione grafica delle funzioni risolte, esercizi

Commento: si noti che la funzione attraversa l’asintoto obliquo nel punto

$(0,0) .$

Gli asintoti obliqui infatti determinano soprattutto il comportamento della funzione quando x tende verso +∞ e -∞, infatti la funzione non attraversa mai l’asintoto obliquo a destra del grafico (x→+∞) e a sinistra di il grafico (x→-∞). Tuttavia è molto raro che la funzione attraversi al centro l’asintoto obliquo, è un caso molto particolare.

Come rappresentare una funzione su un grafico

Esempio di rappresentazione di una funzione

Esercizi risolti per rappresentare le funzioni

Esercizio 1

Esercizio 2

Esercizio 3

Lascia un commento Annulla risposta