Come calcolare le radici di un polinomio? (esercizi risolti)

In questa pagina scoprirai cosa sono le radici di un polinomio e come si calcolano. Inoltre, potrai vedere esempi ed esercizi risolti passo dopo passo sulle radici di un polinomio.

Quali sono le radici di un polinomio?

In matematica le radici (o zeri) di un polinomio sono i valori che annullano il polinomio. Cioè le radici di un polinomio sono tutti quei valori che, valutati nel polinomio, hanno un valore numerico pari a 0.

Infine,

$x=a$

è una radice del polinomio

$P(x)$

Sì

$P(a)=0.$

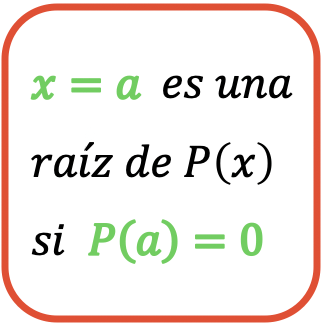
Ad esempio, se abbiamo il seguente polinomio:

$P(x)=x^2-3x+2$

Possiamo verificare che una delle radici del polinomio è 1, poiché il valore numerico del polinomio in x=1 è uguale a zero:

$P(1)=1^2-3\cdot 1+2 = 1-3+2 \color{blue} \bm{= 0}$

D’altra parte 3 non è una radice del polinomio perché non è un valore che annulla il polinomio, o in altre parole il valore numerico del polinomio in x=3 è diverso da zero:

$P(3)=3^2-3\cdot 3+2 = 9-9+2=2 \color{blue} \bm{\neq 0}$

Probabilmente adesso hai capito meglio cos’è la radice di un polinomio, ma non ti piacerebbe sapere quante radici ha un polinomio? Oppure come trovare tutte le radici di un polinomio? Bene, questo è esattamente ciò che vedremo nella prossima sezione.

Come calcolare tutte le radici di un polinomio?

Per trovare tutte le radici di un polinomio, è necessario seguire i seguenti passaggi:

Innanzitutto vengono calcolati tutti i divisori del termine indipendente del polinomio.
In secondo luogo, tutti i valori trovati nel passaggio precedente vengono valutati nel polinomio.
Infine, se nel valutare un numero nel polinomio il suo valore numerico è uguale a zero, detto numero è una radice del polinomio. Altrimenti detto numero non corrisponde ad una radice del polinomio.

Questa procedura si deduce dal teorema del resto , clicca su questo link per scoprire il motivo di questa particolare procedura.

Esempio di calcolo delle radici di un polinomio

Di seguito risolveremo passo dopo passo un esempio in modo che tu possa capire meglio come ricavare le radici di un polinomio.

Quali sono tutte le radici del seguente polinomio?

$P(x) = x^2-5x+6$

Innanzitutto dobbiamo trovare i divisori del termine indipendente, perché ogni radice di un polinomio è anche divisore del termine indipendente. Quindi i divisori di 6 sono:

Divisori di 6: +1, -1, +2, -2, +3, -3

Ricorda che se un numero è un divisore, anche il suo negativo è un divisore. Poiché un numero è divisibile per numeri positivi e negativi.

Pertanto le possibili radici o zeri del polinomio sono: ±1, ±2, ±3. Pertanto, dobbiamo determinare il valore numerico del polinomio per tutti questi valori. E, per fare ciò, sostituiamo questi valori nell’espressione del polinomio dove c’è una x:

$P(1) = 1^2 -5\cdot 1 +6= 1 -5 +6 =2$

$P(-1) = (-1)^2 -5\cdot (-1) +6 =1+5+6 = 12$

$P(2) = 2^2 -5\cdot 2 +6 =4-10+6= \color{blue} \bm{0}$

$P(-2) = (-2)^2 -5\cdot (-2) +6 =4+10+6 =20$

$P(3) = 3^2 -5\cdot 3 +6 =9-15+6=\color{blue} \bm{0}$

$P(-3) = (-3)^2 -5\cdot (-3) +6 =9+15+6 =30$

Quindi il polinomio scompare solo quando la variabile x è +2 o +3, quindi ecco le radici del polinomio:

Radici o zeri del polinomio : +2 e +3

D’altra parte si noti che il polinomio ha tante radici quanto il suo grado, vale a dire che poiché il polinomio è di secondo grado, ha due radici. Nelle proprietà delle radici di un polinomio (sotto), vedremo perché questa caratteristica vale sempre per qualsiasi polinomio.

Abbiamo appena visto un modo per trovare le radici di un polinomio. Esistono però anche altri metodi per raggiungere questo obiettivo, ad esempio si possono trovare le radici di un polinomio anche con la regola di Ruffini. Clicca sul seguente link per vedere esempi della regola Ruffini , qui scoprirai in cosa consiste questo noto metodo e, inoltre, quali sono le differenze tra le due procedure.

Proprietà delle radici di un polinomio

Le radici o zeri di un polinomio hanno le seguenti caratteristiche:

Come abbiamo visto in precedenza, le radici intere (o zeri) di un polinomio sono divisori del termine indipendente del polinomio.

Se conosciamo tutte le radici di un polinomio, possiamo esprimere detto polinomio sotto forma di prodotti di binomi del tipo
$(x-a).$

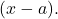
Ad esempio, il polinomio

$P(x) =x^3+3x^2-x-3$

Ha 3 radici che sono

$x=+1, x=-1$

$x=-3.$

Possiamo quindi riscrivere il polinomio sotto forma di 3 moltiplicazioni di fattori, ciascuna formata dalla variabile

$x$

e una radice ha cambiato segno:

$\displaystyle\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60} P(x) =x^3+3x^2-x-3 \ \longrightarrow \ \text{ra\'ices} \begin{cases} x=\color{verd}\bm{+1} \\[2ex] x=\color{vermell}\bm{-1} \\[2ex] x=\color{blau}\bm{-3}\end{cases}$

$\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60}P(x) =x^3+3x^2-x-3 = (x\color{verd}\bm{-1}\color{black})\cdot (x\color{vermell}\bm{+1}\color{black}) \cdot (x\color{blau}\bm{+3}\color{black})$

Questo si chiama fattorizzazione polinomiale. Infatti, una delle principali applicazioni per determinare le radici di un polinomio è che vengono utilizzate per fattorizzarlo. Nel seguente link potrai scoprire in cosa consiste questa particolarissima operazione e, inoltre, potrai esercitarti con esercizi di fattorizzazione polinomiale risolta .

Un polinomio ha tante radici quante ne indica il grado. Quindi, un polinomio di secondo grado avrà 2 radici, un polinomio di terzo grado avrà 3 radici, un polinomio di quarto grado avrà 4 radici e così via.

Se un polinomio non ha un termine indipendente, significa che una delle sue radici è 0. Allora le restanti radici devono essere divisori del coefficiente del monomio di grado più basso.

Ad esempio, il seguente polinomio non ha termini indipendenti:

$P(x) =x^3+x^2-2x$

Quindi una radice del polinomio deve necessariamente essere 0. E le restanti radici sono divisori del coefficiente del termine di grado più basso, cioè -2. Più precisamente, le altre radici lo sono

$x=+1$

$x=-2,$

quindi tutte le radici del polinomio sono:

Radici o zeri del polinomio: 0, +1 e -2

Quando non è possibile determinare le radici di un polinomio si dice che è irriducibile.

Ad esempio, proveremo a calcolare le radici del seguente polinomio:

$P(x) =x^2+3x-1$

Le uniche radici possibili del polinomio sono i divisori di -1, cioè -1 e +1. Valutiamo quindi il polinomio a questi valori:

$P(1) = 1^2 +3\cdot 1 -1= 1 +3 -1 =3 \neq 0$

$P(-1) = (-1)^2 +3\cdot (-1)-1 =1-3-1 =-3 \neq 0$

In nessun caso il polinomio si cancella, quindi non ha radici e, quindi, è un polinomio irriducibile.

Quando il polinomio è formato dal prodotto di più polinomi, non è necessario fare questo prodotto per calcolare le radici, ma le radici del polinomio sono le radici di ciascun fattore moltiplicate.

Ad esempio, se abbiamo il seguente polinomio:

$P(x) = (x-2) \cdot (x+1)$

Dalla seconda proprietà delle radici dei polinomi si deduce che la radice del polinomio di sinistra è +2 e la radice del polinomio di destra è -1.

$\displaystyle (x-2) \ \longrightarrow \ \text{ra\'iz} \ x=+2$

$\displaystyle (x+1) \ \longrightarrow \ \text{ra\'iz} \ x=-1$

Quindi le radici del polinomio risultante dalla moltiplicazione dei due fattori sono le rispettive radici, cioè +2 e -1.

$\displaystyle P(x) = (x-2) \cdot (x+1) \ \longrightarrow \ \text{ra\'ices} \ \begin{cases}x=+2 \\[2ex] x=-1 \end{cases}$

Esercizi risolti sulle radici dei polinomi

Esercizio 1

Determina se

$x = -4$

è una radice del seguente polinomio:

$P(x)=x^3+2x^2-11x-12$

Vedi la soluzione

Per scoprire se

$x=-4$

è una radice del polinomio, dobbiamo valutarlo su quel valore. Ancora:

$\begin{aligned}P(-4)& =(-4)^3+2\cdot (-4)^2-11\cdot (-4) -12 \\[2ex] & = -64+2\cdot 16 +44 -12 \\[2ex] & = -64+32+44 -12 \\[2ex] & = 0 \end{aligned}$

Il valore numerico del polinomio in

$x=-4$

è zero, quindi è effettivamente una radice del polinomio.

Esercizio 2

Calcola tutte le radici del seguente polinomio:

$P(x)=x^2-3x+2$

Vedi la soluzione

Innanzitutto, per trovare le possibili radici del polinomio, dobbiamo trovare i divisori del termine indipendente. Quindi i divisori di 2 sono:

Divisori di 2: +1, -1, +2, -2

Le possibili radici o zeri del polinomio sono quindi ±1 e ±2. Dobbiamo quindi calcolare quanto vale il polinomio in tutti questi valori:

$P(1)=1^2-3\cdot 1+2 =1-3+2=0$

$P(-1)=(-1)^2-3\cdot (-1)+2 =1+3+2=6$

$P(2)=2^2-3\cdot 2+2 =4-6+2=0$

$P(-2)=(-2)^2-3\cdot (-2)+2 =4+6+2=12$

Pertanto, il polinomio scompare quando x è +1 o +2, quindi ecco le radici del polinomio:

Radici o zeri del polinomio : +1 e +2

Esercizio 3

Trova le radici del seguente polinomio:

$P(x)=x^3-x^2-4x+4$

Vedi la soluzione

Dobbiamo prima trovare i divisori del termine indipendente, poiché la radice di un polinomio è anche un divisore del termine indipendente. Quindi i divisori di 4 sono:

Divisori di 4: +1, -1, +2, -2, +4, -4

Le possibili radici o zeri del polinomio sono quindi ±1, ±2 e ±4. Dobbiamo quindi trovare il valore numerico del polinomio in tutti questi valori:

$P(1)=1^3-1^2-4\cdot 1+4 =1-1-4+4=0$

$P(-1)=(-1)^3-(-1)^2-4\cdot (-1)+4 =-1-1+4+4=6$

$P(2)=2^3-2^2-4\cdot 2+4 =8-4-8+4=0$

$P(-2)=(-2)^3-(-2)^2-4\cdot (-2)+4 =-8-4+8+4=0$

$P(3)=3^3-3^2-4\cdot 3+4 =27-9-12+4=10$

$P(-3)=(-3)^3-(-3)^2-4\cdot (-3)+4 =-27-9+12+4=20$

Pertanto, il polinomio scompare solo quando x è +1, +2 o -2, quindi ecco le radici del polinomio:

Radici o zeri del polinomio : +1, +2 e -2

Esercizio 4

Trova le radici del seguente polinomio:

$P(x)=x^3-6x^2+8x$

Vedi la soluzione

In questo caso il polinomio non ha termini indipendenti. Pertanto, secondo la quarta proprietà delle radici spiegata sopra, sappiamo che una delle radici del polinomio deve essere 0.

Radici del polinomio:

$x=0$

Inoltre, in questo caso, le possibili radici non sono i divisori del termine indipendente, bensì quelle del coefficiente del termine di grado più basso, cioè 8:

Divisori di 8: +1, -1, +2, -2, +4, -4, +8, -8

Quindi le possibili radici o zeri del polinomio sono ±1, ±2, ±4 e ±8. Dobbiamo quindi calcolare il valore numerico del polinomio a tutti questi valori:

$P(1)=1^3-6\cdot 1^2+8\cdot 1 = 1-6+8=3$

$P(-1)=(-1)^3-6\cdot (-1)^2+8\cdot (-1) = -1-6-8=-15$

$P(2)=2^3-6\cdot 2^2+8\cdot 2 = 8-24+16=0$

$P(-2)=(-2)^3-6\cdot (-2)^2+8\cdot (-2) = -8-24-16=-48$

$P(4)=4^3-6\cdot 4^2+8\cdot 4 = 64-96+32=0$

$P(-4)=(-4)^3-6\cdot (-4)^2+8\cdot (-4) = -64-96-32=-192$

$P(8)=8^3-6\cdot 8^2+8\cdot 8 = 512-384+64=192$

$P(-8)=(-8)^3-6\cdot (-8)^2+8\cdot (-8) = -512-384-64=-960$

Quindi il polinomio scompare quando x è +2 o +4, quindi questi valori sono le radici del polinomio. Dobbiamo però aggiungere anche la radice 0 che abbiamo trovato all’inizio del problema. In conclusione, tutte le radici del polinomio sono:

Radici o zeri del polinomio : 0, +2 e +4

Esercizio 5

Utilizza le proprietà delle radici dei polinomi per calcolare le radici del seguente polinomio:

$P(x)=(x-1)(x+3)(x^2-x-2)$

Vedi la soluzione

Come abbiamo visto nella sesta proprietà delle radici, quando il polinomio è formato dal prodotto di fattori, non è necessario calcolare tutte le radici, poiché le radici dell’intero polinomio sono le radici di ciascun fattore.

Inoltre, dalla seconda proprietà delle radici dei polinomi, possiamo dedurre che la radice del primo fattore è +1 e la radice del secondo fattore è -3.

$\displaystyle (x-1) \ \longrightarrow \ \text{ra\'iz} \ x=+1$

$\displaystyle (x+3) \ \longrightarrow \ \text{ra\'iz} \ x=-3$

Quindi dobbiamo solo trovare le radici dell’ultimo fattore. Per fare ciò troviamo i divisori del termine indipendente (-2):

Divisori di -2: +1, -1, +2, -2

Quindi le possibili radici o zeri dell’ultimo polinomio sono ±1 e ±2. Con cui dobbiamo calcolare il valore numerico di detto polinomio in tutti questi valori:

$q(x)= x^2-x-2$

$q(1)=1^2-1-2=1-1-2=-2$

$q(-1)=(-1)^2-(-1)-2=1+1-2=0$

$q(2)=2^2-2-2=4-2-2=0$

$q(-2)=(-2)^2-(-2)-2=4+2-2=4$

Le radici del polinomio a destra sono quindi -1 e 2.

Pertanto, le radici dell’intero polinomio sono tutte le radici trovate:

Radici o zeri del polinomio : +1, -1, +2, -3

Radici di un polinomio

Quali sono le radici di un polinomio?

Come calcolare tutte le radici di un polinomio?

Esempio di calcolo delle radici di un polinomio

Proprietà delle radici di un polinomio

Esercizi risolti sulle radici dei polinomi

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Lascia un commento Annulla risposta