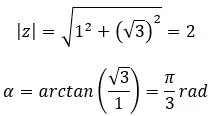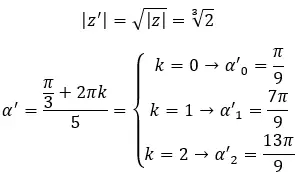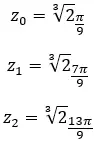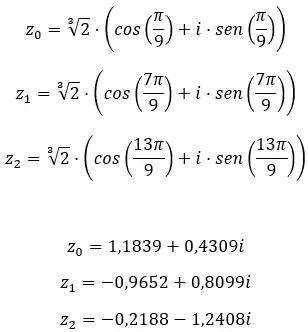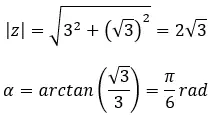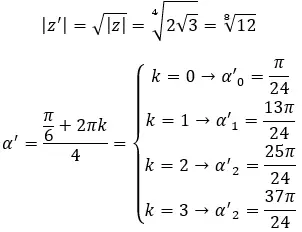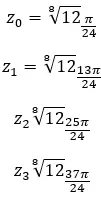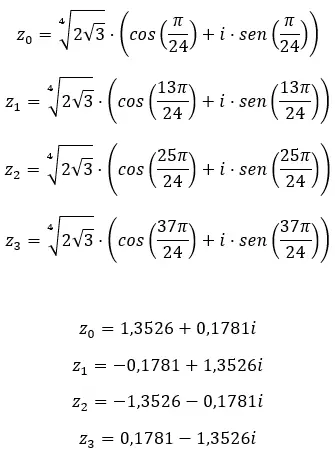Calcolare le radici dei numeri complessi è abbastanza semplice. Beh, una volta compresa la procedura, risulta abbastanza ripetitiva. Successivamente lo spiegheremo e ti daremo un esempio, così potrai imparare come applicarlo in esercizi reali.
radici n-esime di numeri complessi
Il concetto di radice n-esima equivale a dire radice di ordine n, quindi lo stesso metodo si usa per calcolare la radice quadrata e la radice quinta di un numero complesso. Naturalmente, il numero di soluzioni cambierà a seconda di questo ordine.
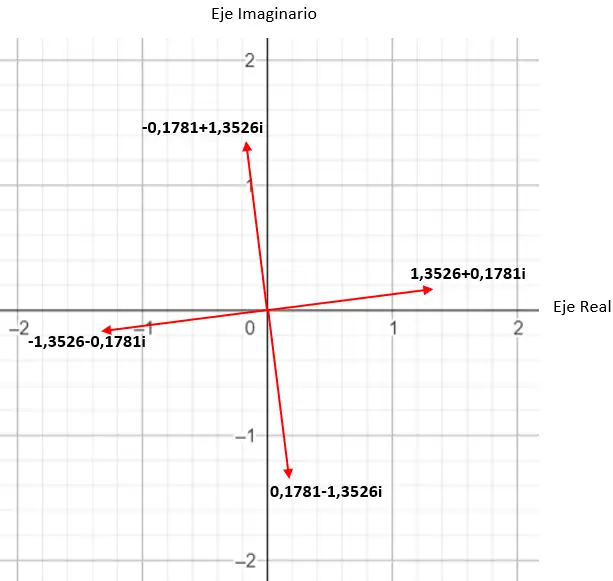
Se ad esempio calcoliamo la radice quarta di un complesso otteniamo 4 soluzioni diverse. E se lo esprimiamo nel piano complesso , vediamo che si forma un poligono regolare di 4 lati, centrato nell’origine del piano. Si tratta di una proprietà molto interessante, che vedremo in dettaglio più avanti (nella sezione degli esempi).
Ora che abbiamo chiarito questo concetto, vedremo come calcolare la radice di un numero complesso in forma polare (usare questa notazione è la più comoda per risolvere una radice). Semplicemente, devi calcolare la radice del modulo ed esprimere l’argomento in termini di n. In altre parole, la radice del seguente numero complesso (z):
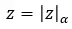
Questi importi da calcolare:
- Modulo: l’ennesima radice del modulo iniziale.
- Argomento: aggiungi 2πk in radianti o 360k in gradi all’argomento e dividi per n.
Matematicamente per calcolare modulo e argomento utilizziamo le seguenti due formule:
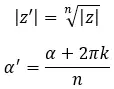
Dove, k = 0, 1, 2, …, n-1.
E, pertanto, esprimiamo il risultato come segue:
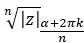
Per intenderci, le n soluzioni che otterremo risolvendo questa radice saranno formate dallo stesso modulo e n argomenti diversi.
Esempi di calcolo delle radici n-esime di complessi
Vedremo ora alcuni esempi sul calcolo delle radici n-esime di numeri complessi. Ti consigliamo di provare a risolverli da solo e, una volta terminato, di esaminare la correzione. Non dimenticare che il metodo è spiegato poco sopra.
Trova la terza radice del numero complesso: 1 + i √3 .
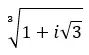
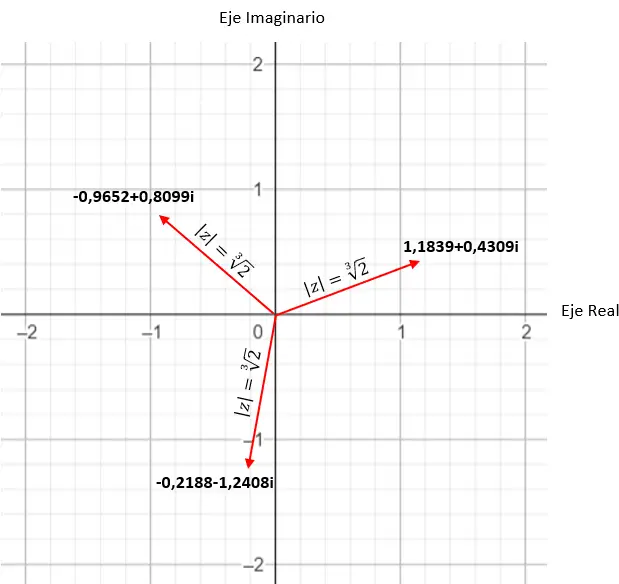
Trova la quarta radice del numero complesso: 3+i √ 3 .
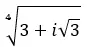
Conoscere le radici dei numeri complessi
- Numeri complessi
- Operazioni su numeri complessi
- poteri complessi
- Proprietà dei numeri complessi