Matrice regolare o invertibile

In questa pagina troverai la spiegazione di una matrice regolare o invertibile e come sapere quando è possibile eseguire l’inversione di una matrice e quando no. Inoltre, vedrai anche diversi esempi di matrici regolari per comprendere appieno il concetto e, infine, ti mostreremo tutte le proprietà di questo tipo di matrice.

Cos’è una matrice regolare?

La definizione di matrice regolare è la seguente:

Una matrice regolare è una matrice quadrata che può essere invertita, ovvero si può calcolare l’inverso di detta matrice. Pertanto, il suo determinante è diverso da zero (0).

Le matrici regolari sono anche chiamate matrici invertibili, non singolari o non degeneri .

La matrice opposta alla matrice regolare è la matrice singolare o degenere.

Quindi, per sapere quando una matrice è regolare o singolare, cioè quando una matrice è invertibile o meno, è sufficiente risolvere il determinante della matrice:

Se il determinante della matrice è diverso da zero, la matrice è regolare o invertibile.

Se il determinante della matrice è uguale a zero la matrice è singolare ovvero non invertibile.

In conclusione, calcolare il determinante di una matrice è il modo più semplice per sapere se la matrice ha un’inversa o meno, quindi questo è ciò che consigliamo per determinare l’invertibilità di qualsiasi matrice.

Se vuoi sapere come invertire una matrice, puoi consultare la formula della matrice inversa , che spiega passo dopo passo come invertire una matrice, e troverai anche diversi esempi ed esercizi risolti per esercitarti.

Esempi di matrici regolari o invertibili

Una volta visto il significato di matrice regolare o invertibile, vediamo alcuni esempi di matrici regolari di diverse dimensioni:

Esempio di matrice 2×2 regolare o invertibile

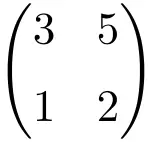
Possiamo verificare che si tratta di una matrice regolare calcolandone il determinante:

$\displaystyle\begin{vmatrix} 3&5 \\[1.1ex] 1 & 2\end{vmatrix}=1\bm{\neq 0}$

Il determinante della matrice di ordine 2 è diverso da 0, quindi è una matrice regolare.

Esempio di matrice 3×3 regolare o invertibile

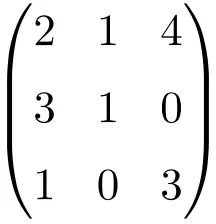
esempio di matrice regolare o invertibile di dimensione 3x3

Dobbiamo fare il determinante della matrice per verificare che sia una matrice invertibile:

$\displaystyle\begin{vmatrix} 2&1&4\\[1.1ex] 3&1&0\\[1.1ex] 1&0&3\end{vmatrix}=-7\bm{\neq 0}$

Il determinante della matrice di ordine 3 dà un risultato diverso da 0, quindi è una matrice regolare.

Esempio di matrice 4×4 regolare o invertibile

esempio di matrice regolare o invertibile di dimensione 4x4

Prendendo il determinante della matrice si vede che si tratta di una matrice regolare:

$\displaystyle\begin{vmatrix} 1&3&-2&0\\[1.1ex] 2&-1&0&5\\[1.1ex] 1&3&1&2\\[1.1ex] 0&-1&2&4\end{vmatrix}=-49\bm{\neq 0}$

Il determinante della matrice di ordine 4 non è zero, è quindi una matrice invertibile.

Attenzione: Se hai dubbi sui calcoli dei determinanti puoi consultare la pagina come calcolare un determinante .

Proprietà delle matrici regolari o invertibili

Le matrici regolari o invertibili sono molto importanti per l’algebra lineare e ciò è dovuto alle seguenti caratteristiche:

Se A è una matrice invertibile, lo è anche la sua matrice trasposta o trasposta. Inoltre, la matrice inversa della trasposizione è uguale alla trasposizione dell’inverso.

$\displaystyle \left(A^t\right)^{-1}=\left(A^{-1}\right)^t$

L’intervallo di una matrice regolare è sempre il massimo possibile, o in altre parole l’intervallo equivale alla dimensione della matrice.

Il prodotto di matrice tra due matrici invertibili dà origine ad un’altra matrice regolare. Questa condizione può essere facilmente dimostrata con le proprietà dei determinanti:

$\displaystyle \left.\begin{array}{l}\text{det}(A\cdot B)=\text{det}(A)\cdot\text{det}(B) \\[2ex] \text{det}(A)\neq 0 \quad ; \quad \text{det}(B) \neq 0 \end{array}\right\} \longrightarrow \ \text{det}(A\cdot B) \neq 0$

Ogni matrice ortogonale è allo stesso tempo una matrice regolare.

Sia A la matrice che rappresenta un sistema di equazioni lineari
$(Ax=b)$

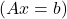
, se A è una matrice regolare, il sistema ha un’unica soluzione, è quindi un sistema delle determinanti compatibili (SCD).

Inoltre, se il sistema è un sistema omogeneo
$(Ax=0)$

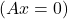
e A può essere invertito, la soluzione del sistema è banale:

$x=0.$

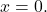
Le colonne e le righe di una matrice regolare sono linearmente indipendenti l’una dall’altra.

Tutti gli autovalori (o autovalori) di una matrice regolare o invertibile sono diversi da zero.

Matrice invertibile regolare d'oro