Cosa sono i vettori (matematica)? -Matorietà

In questa pagina troverai tutto sui vettori: cosa sono, le loro caratteristiche, come si calcolano, come eseguire operazioni con i vettori, i diversi tipi che esistono,…

Cos’è un vettore?

La definizione matematica di un vettore è la seguente:

In matematica, un vettore è un segmento orientato che va da un punto (chiamato origine) a un altro punto (chiamato fine).

Ad esempio, nel grafico seguente, puoi vedere che il vettore

$\vv{AB}$

Ha come origine il punto A e come punto finale il punto B.

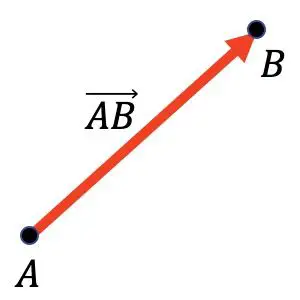
I vettori vengono utilizzati principalmente in matematica, in particolare in geometria e fisica, per rappresentare graficamente le forze vettoriali.

Caratteristiche di un vettore

Una volta visto qual è il significato matematico dei vettori, vediamo ora quali sono le loro proprietà.

Ogni vettore ha le seguenti caratteristiche geometriche:

Direzione : La direzione di un vettore è la direzione della linea che contiene il vettore o qualsiasi linea parallela ad esso. In altre parole, la direzione di un vettore è la linea su cui giace.
Direzione : la direzione di un vettore è l’orientamento di detto vettore, indicato dalla sua freccia.
Modulo (o grandezza): il modulo di un vettore è la sua lunghezza, e corrisponde al valore numerico del vettore. Pertanto, quanto più grande è il vettore, tanto maggiore è la quantità del vettore che rappresenta.
Punto di applicazione : il punto di applicazione di un vettore è l’origine di detto vettore.

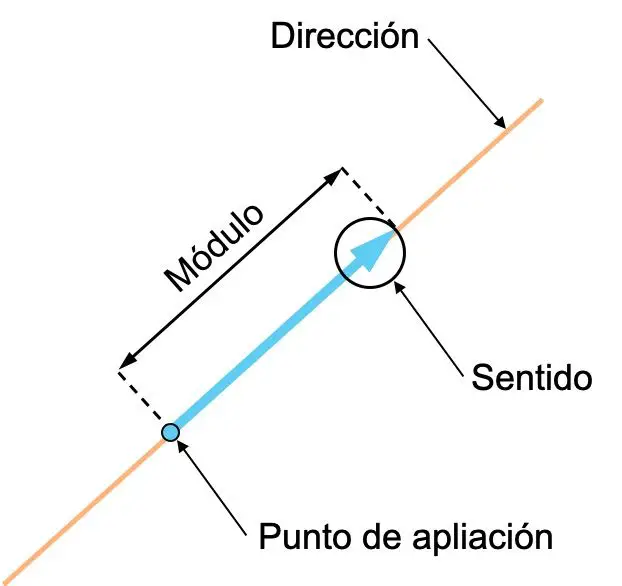
Le nozioni di direzione e direzione di un vettore sono spesso confuse, quindi è importante distinguere la differenza tra loro. Guarda l’esempio seguente con due vettori, entrambi hanno la stessa direzione ma il loro significato è diverso:

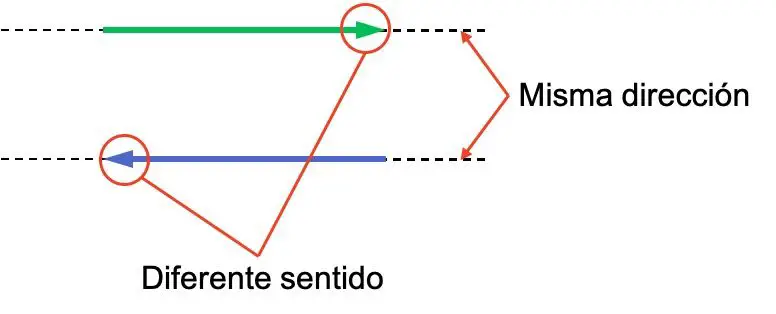
significato del significato e della direzione di un vettore

I due vettori hanno la stessa direzione perché sono paralleli. Invece, le loro direzioni sono opposte perché sono rivolte all’indietro.

Componenti di un vettore

Abbiamo appena visto che i vettori sono rappresentati graficamente dalle frecce, ma i vettori possono anche essere rappresentati numericamente dalle componenti (o coordinate) di un vettore.

Ad esempio, se abbiamo il seguente vettore rappresentato in un grafico:

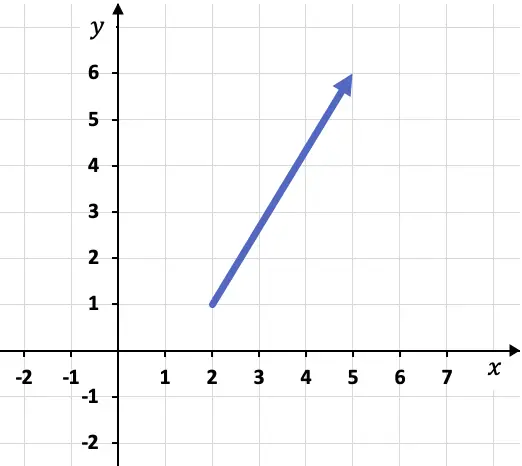
Per calcolare le componenti del vettore dobbiamo innanzitutto individuare le coordinate della sua origine e della sua fine, cioè i punti in cui inizia e dove finisce. In questo caso, l’origine e la fine del vettore sono:

Origine del vettore: A(2,1)

Punto finale del vettore: B(5,6)

Quindi, per trovare le coordinate o le componenti del vettore, sottrai semplicemente il punto finale meno l’origine:

$\begin{aligned} \vv{AB} & = B- A \\[2ex] & = (5,6)- (2,1) \\[2ex] &= (5-2 \ , \ 6-1) \\[2ex] &= (3,5) \end{aligned}$

Pertanto le componenti del vettore rappresentato nel grafico sono:

$\vv{\bm{AB}}\bm{=(3,5)}$

Operazioni vettoriali

aggiungendo il vettore

Per sommare numericamente due vettori, è necessario sommare le rispettive componenti. O in altre parole, si sommano le coordinate X dei due vettori e coincidono con le coordinate Y.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} + \vv{\text{v}} = (\text{u}_x + \text{v}_x \ , \ \text{u}_y + \text{v}_y) \end{array} \end{empheq}$

Per poter vedere come è fatto, aggiungeremo i seguenti due vettori:

$\vv{\text{u}} = (2,3) \qquad \vv{\text{v}}=(4, -1)$

$\begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(2,3) +(4,-1) \\[2ex] & = (2+4,3+(-1)) \\[2ex] & = \bm{(6,2)} \end{aligned}$

È inoltre possibile aggiungere due vettori dalle loro rappresentazioni grafiche. Per questo normalmente viene utilizzata la regola o legge del parallelogramma, ma esistono molti metodi. Puoi vedere esempi ed esercizi risolti su come sommare graficamente due vettori qui.

sottrazione vettoriale

Per sottrarre analiticamente due vettori, è necessario sottrarre le rispettive componenti. Cioè, le coordinate X dei due vettori vengono sottratte l’una dall’altra e lo stesso delle coordinate Y.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} - \vv{\text{v}} = (\text{u}_x - \text{v}_x \ , \ \text{u}_y - \text{v}_y) \end{array} \end{empheq}$

Ad esempio, sottraiamo i due vettori seguenti:

$\vv{\text{u}} = (3,1) \qquad \vv{\text{v}}=(2, -4)$

$\begin{aligned} \vv{\text{u}} - \vv{\text{v}}& =(3,1) -(2,-4) \\[2ex] & = (3-2,1-(-4)) \\[2ex]& = (3-2,1+4) \\[2ex] & = \bm{(1,5)} \end{aligned}$

Come l’addizione, puoi anche sottrarre 2 vettori usando le loro rappresentazioni. Per questo, di solito viene utilizzata la regola o legge del triangolo, ma esistono diversi metodi. Puoi vederli tutti con esempi ed esercizi risolti su come sottrarre graficamente due vettori .

modulo di un vettore

Come abbiamo visto all’inizio di questa pagina, la grandezza di un vettore corrisponde alla lunghezza di quel vettore. Ebbene, la lunghezza (o grandezza) di un vettore può essere determinata dalle sue componenti.

Considera qualsiasi vettore:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

Per trovare il modulo di un vettore nel piano, dobbiamo applicare la seguente formula:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2} \end{empheq}$

Ad esempio, calcoleremo la grandezza del seguente vettore utilizzando la formula:

$\vv{\text{u}} = (3,-4)$

$\lvert \vv{\text{u}} \rvert =\sqrt{3^2+(-4)^2} = \sqrt{9+16}=\sqrt{25} = \bm{5}$

Anche se sembra molto semplice, determinare la grandezza di un vettore può essere complicato. Se vuoi vedere altri esempi ed esercitarti con gli esercizi risolti del modulo di un vettore , ti consigliamo di visitare questa pagina collegata.

Moltiplicazione di un vettore per uno scalare

Per calcolare numericamente il prodotto di un vettore per un numero (o uno scalare), ciascuna componente del vettore deve essere moltiplicata per quel numero.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}\vv{\text{u}} = (\text{u}_x,\text{u}_y)\\[4ex]k\cdot \vv{\text{u}} =(k\cdot \text{u}_x \ , \ k\cdot \text{u}_y) \end{array} \end{empheq}$

Nel seguente esempio generico si vede come la direzione del vettore viene mantenuta indipendentemente dal segno dello scalare. D’altra parte, la direzione del vettore dipende dal segno del numero che moltiplica.

moltiplicazione o prodotto di un numero o di uno scalare per un vettore

Di seguito puoi vedere un esempio numerico di come trovare il prodotto di un vettore per un numero:

$\vv{\text{u}} =(3,-2)$

$4\cdot \vv{\text{u}} =(4 \cdot 3 \ , \ 4 \cdot (-2)) = \bm{(12,-8)}$

Prodotto scalare

Nella geometria analitica, il prodotto scalare è un’operazione vettoriale che moltiplica due vettori e li trasforma in un numero reale.

Pertanto, la formula per il prodotto scalare di due vettori è la seguente:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \cdot \vv{\text{v}} = \text{u}_x\cdot \text{v}_x + \text{u}_y\cdot \text{v}_y \end{empheq}$

Di seguito è riportato un esempio in cui viene calcolato il risultato del prodotto scalare tra due vettori:

$\vv{\text{u}} = (4,2) \qquad \vv{\text{v}} = (-1,3)$

$\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(4,2)\cdot (-1,3) \\[1.5ex]&=4\cdot (-1) + 2 \cdot 3 \\[1.5ex] & = -4+6 \\[1.5ex] & =\bm{10} \end{aligned}$

In questo collegamento puoi vedere altri esempi del prodotto scalare . Inoltre, troverai un altro modo per trovare il prodotto scalare tra due vettori, le proprietà di questo tipo di operazione con i vettori e gli esercizi risolti passo dopo passo.

prodotto vettoriale

Sebbene siano molto simili nel nome, il prodotto scalare e il prodotto incrociato sono completamente diversi.

Il prodotto incrociato , chiamato anche prodotto incrociato, è un’operazione tra due vettori nello spazio (in R3), cioè sono vettori a tre coordinate.

Quindi, se abbiamo due vettori tridimensionali:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

Il prodotto vettoriale dei due vettori è uguale al risultato del seguente determinante 3×3:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix} \end{empheq}$

dove i vettori

$\vv{i}, \vv{j},\vv{k}$

sono i versori nelle direzioni rispettivamente degli assi X, Y, Z.

Inoltre, la direzione del vettore risultante è perpendicolare ai due vettori moltiplicati.

Come puoi intuire, risolvere questo tipo di operazioni è più difficile delle precedenti e, per questo motivo, abbiamo un’intera pagina con una spiegazione dettagliata di come si calcola il prodotto incrociato tra due vettori. Pertanto, se sei interessato, ti consigliamo di visitarlo e di esercitarti con gli esercizi sui prodotti vettoriali risolti .

prodotto misto

Il prodotto misto di tre vettori, chiamato anche prodotto triplo punto, è una moltiplicazione successiva tra tre vettori che coinvolge due diversi tipi di operazioni: il prodotto scalare e il prodotto vettoriale. Quindi, la combinazione delle due operazioni vettoriali dà uno scalare (un numero reale).

Concretamente, il prodotto misto consiste nel calcolare il prodotto vettoriale di due vettori e, successivamente, moltiplicare vettorialmente il risultato ottenuto per un terzo vettore. Guarda la formula:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.3pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}}) \end{empheq}$

Come per il prodotto vettoriale, risolvere il prodotto misto tra vettori non è facile. Per questo motivo ti consigliamo di dare un’occhiata a questa spiegazione del prodotto misto di tre vettori , dove troverai esempi, esercizi risolti e il significato geometrico di questa operazione vettoriale.

tipi di vettori

Esistono molti tipi diversi di vettori, ma le definizioni più importanti da conoscere sono:

Vettore unitario : vettore il cui modulo è uguale a 1.
Vettore fisso : un vettore è fisso quando l’origine del vettore è applicata a un punto fisso.
Vettore libero : Un vettore è libero quando il suo punto di applicazione non è definito, ma è un punto libero.
Vettori collineari : due o più vettori sono collineari se condividono la stessa linea d’azione (linea dove si trova il vettore).
Vettori equivalenti : due vettori sono equipollini se hanno la stessa dimensione, lo stesso senso e la stessa direzione (anche se possono avere punti di applicazione diversi).
Vettori concatenati : I vettori concatenati sono vettori equipollini che agiscono anche sulla stessa linea.
Vettori opposti : due vettori sono opposti se hanno la stessa grandezza e la stessa direzione ma direzione diversa.
Vettore posizione : il vettore posizione è il vettore la cui origine è il punto (0,0) (origine delle coordinate).
Vettori concorrenti : due o più vettori sono concorrenti quando le loro linee d’azione passano per lo stesso punto, cioè si intersecano.
Vettori paralleli : due o più vettori sono paralleli se hanno la stessa direzione, indipendentemente dalla loro direzione.
Vettori perpendicolari : Due vettori sono perpendicolari (o ortogonali) quando le loro direzioni formano un angolo di 90º.
Vettori ortonormali : Due o più vettori sono ortonormali se sono perpendicolari tra loro e, inoltre, sono unitari (la loro grandezza è uguale all’unità).
Vettori complanari : due o più vettori sono complanari se contenuti nello stesso piano.

Angolo tra due vettori

Per trovare l’angolo tra due vettori dati, dobbiamo applicare la seguente formula:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

Oro

$\lvert \vv{\text{u}} \rvert$

$\lvert \vv{\text{v}} \rvert$

sono i moduli dei vettori

$\vv{\text{u}}$

$\vv{\text{v}}$

rispettivamente.