Quadrato di una somma (o somma al quadrato)

In questa pagina troverai la formula del quadrato di una somma, cioè dell’identità notevole (a+b) ² . Potrai anche vedere esempi ed esercizi risolti di somme quadrate. E, inoltre, scoprirete le proprietà geometriche nascoste in questo straordinario prodotto.

Qual è il quadrato di una somma?

Il quadrato di una somma è una delle identità notevoli (o prodotti notevoli), quindi è una regola matematica che consente di calcolare rapidamente la potenza di un binomio con due termini positivi al quadrato.

Pertanto, il quadrato di una somma è costituito da due termini diversi sommati insieme e al quadrato, ovvero l’espressione algebrica del quadrato di una somma è (a+b) ² .

Formula per il quadrato di una somma

Data la definizione matematica di questo notevole tipo di identità, vedremo ora quale è la formula del quadrato di una somma :

Quindi il quadrato di una somma è uguale al quadrato del primo termine, più il doppio del prodotto del primo per il secondo, più il quadrato del secondo.

Quindi, per risolvere una somma quadrata, non è sufficiente elevare ciascuna addizione a due, ma, inoltre, le due addizioni devono essere moltiplicate insieme e per 2.

Questo è importante da ricordare, perché un errore molto comune quando si sommano i quadrati è dimenticare il prodotto tra i due termini e calcolare solo i quadrati:

Ricordatevi di non tralasciare nessun termine dalla formula!

Ricordiamo d’altronde che la formula della sottrazione al quadrato (o quadrato di una sottrazione) è molto simile a quella che abbiamo appena visto, ma presenta una differenza che cambia completamente il risultato. Se non sei sicuro di come sia, puoi controllare qui qual è la formula di sottrazione al quadrato e come viene applicata.

Esempi di quadrati somma

Ecco alcuni esempi pratici per vedere come elevare al quadrato una somma:

Esempio 1

Calcola la seguente somma al quadrato applicando la formula:

$(x+5)^2$

La formula per una somma quadrata è:

$(a+b)^2=a^2+2ab+b^2$

Dobbiamo prima individuare i parametri

$a$

$b$

della formula. In questo caso,

$a$

rappresenta il

$x$

della coppia e

$b$

corrisponde al numero 5:

$\left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}$

Bene, poiché ora conosciamo i valori di

$a$

e di

$b,$

Possiamo applicare la formula per trovare il risultato del quadrato della somma:

quadrato di una somma di prodotti notevoli

Esempio 2

Risolvi la seguente espressione per il quadrato di una somma:

$(3x+4)^2$

La formula del quadrato di una somma è:

$(a+b)^2=a^2+2ab+b^2$

Quindi in questo problema

$a$

è il monomio

$3x$

E d’altra parte,

$b$

è il termine indipendente 4:

$\begin{array}{c} a=3x \\[2ex] b=4 \end{array}$

Infine, una volta individuati i valori di

$a$

e di

$b$

, applichiamo la formula della somma quadrata per risolvere il prodotto notevole:

$\begin{aligned} (3x+4)^2 & =(3x)^2+2 \cdot 3x\cdot 4+4^2 \\[2ex] & =9x^2+24x+16 \end{aligned}$

Dimostrazione della formula del quadrato di una somma

Poi dedurremo la formula che abbiamo appena visto dal quadrato di una somma, in modo che tu capisca da dove viene.

Partendo da un binomio positivo elevato a 2:

$(a+b)^2$

La potenza sopra è ovviamente equivalente al fattore

$(a+b)$

moltiplicato per se stesso:

$(a+b)^2=(a+b)\cdot (a+b)$

Quindi moltiplichiamo le due parentesi utilizzando la proprietà distributiva:

$\begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}$

Infine, dai termini risultanti, raggruppiamo quelli simili:

$a^2+ab+ba+b^2 = a^2+2ab+b^2$

E siamo già arrivati all’espressione polinomiale della formula, quindi è dimostrato:

$(a+b)^2= a^2+2ab+b^2$

Anche se può essere difficile da credere, la formula del quadrato di una somma funziona anche per fattorizzare i polinomi quadratici . Nel caso non sapessi di cosa si tratta, la fattorizzazione polinomiale è una procedura spesso utilizzata in matematica per semplificare l’espressione di un polinomio. Scopri come fare cliccando sul link qui sopra.

Interpretazione geometrica del quadrato di una somma

Finora abbiamo visto come si calcola matematicamente il quadrato di una somma, ma questo notevole prodotto può essere interpretato anche geometricamente.

Osserva il seguente quadrato i cui lati misurano

$a+b:$

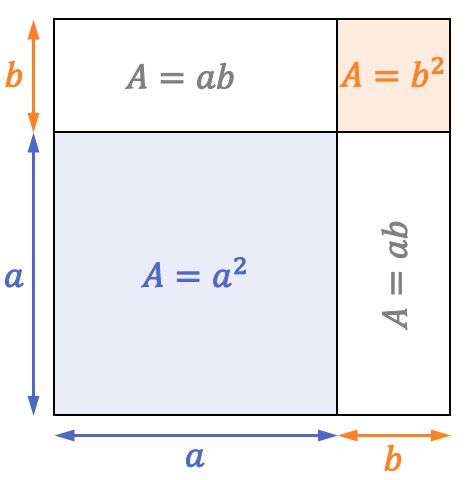
Interpretazione geometrica quadrata di una somma

L’area di un quadrato è uguale alla lunghezza di uno dei suoi lati al quadrato. Pertanto, come è il lato del quadrato precedente

$a+b,$

la sua area (o superficie) è uguale a

$(a+b)^2.$

Ebbene, come puoi vedere nella rappresentazione del quadrato, un quadrato con un’area di

$a^2,$

rettangoli con due aree

$ab,$

e un altro quadrato di superficie

$b^2.$

Pertanto la formula per la somma dei quadrati è soddisfatta anche dal punto di vista geometrico:

$(a+b)^2=a^2+2ab+b^2$

Risolti problemi del quadrato di una somma

Poi ti lasciamo con diversi esercizi di somme di quadrati risolti passo dopo passo in modo che tu possa esercitarti e così finire di comprendere il concetto. Potete scriverci tutte le vostre domande nei commenti, e saremo felici di rispondervi. 💭💭💭

Esercizio 1

Determinare le seguenti somme al quadrato:

$\text{A)} \ (x+3)^2$

$\text{B)} \ (2+6x)^2$

$\text{C)} \ \left(x^2+7\right)^2$

$\text{D)} \ (5x+8y)^2$

vedi soluzione

Per risolvere tutte le identità notevoli del problema è sufficiente applicare la formula del quadrato di una somma:

$(a+b)^2=a^2+2ab+b^2$

$\text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}$

$\text{B)} \ \begin{aligned}(2+6x)^2 & =2^2+2\cdot 2\cdot 6x +(6x)^2\\[2ex] & = \bm{4+24x+36x^2}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}$

$\text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}$

Esercizio 2

Risolvi i seguenti quadrati somma di due termini applicando la formula:

$\text{A)} \ \left(4x^2+2y^3\right)^2$

$\text{B)} \ \displaystyle \left(\sqrt{2x}+\sqrt{8x}\right)^2$

$\text{C)} \ \displaystyle \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2$

vedi soluzione

Per calcolare tutti i prodotti notevoli del problema è necessario utilizzare la formula della somma quadrata:

$(a+b)^2=a^2+2ab+b^2$

$\text{A)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}$

Nella sezione B) bisogna ricordare che se una radice è quadrata si semplifica:

$\text{B)} \ \begin{aligned}\left(\sqrt{2x}+\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2+2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x+2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x+2\sqrt{16x^2} \\[2ex] &= 10x+2\cdot 4x = \\[2ex] & = 10x +8x \\[2ex] & = \bm{18x}\end{aligned}$

I monomi dell’ultima somma al quadrato hanno coefficienti frazionari, quindi per risolverlo dobbiamo utilizzare anche le proprietà delle frazioni:

$\text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}$

Esercizio 3

Trova la seguente potenza applicando la formula del quadrato di una somma e senza usare la calcolatrice:

$17^2$

vedi soluzione

Innanzitutto il numero diciassette può essere scomposto nella somma di 10 più 7:

$17^2=(10+7)^2$

Quindi abbiamo convertito la potenza in una somma quadrata. Pertanto, ora possiamo applicare la formula corrispondente:

$\begin{aligned}(10+7)^2 & = 10^2+2\cdot 10 \cdot 7 +7^2 \\[2ex] & =100+140+49\\[2ex] & =289 \end{aligned}$

In breve, il risultato del potenziamento è:

$17^2=\bm{289}$

Come hai visto in questo esercizio, la formula della somma quadrata è utile anche per calcolare le potenze di grandi numeri senza usare la calcolatrice.

Quadrato di una somma di 3 termini

A volte potremmo scoprire che dobbiamo risolvere il quadrato di tre termini aggiunti, cioè (a+b+c) ² . Logicamente in questi casi non possiamo usare la formula che abbiamo spiegato, perché all’interno delle parentesi abbiamo un trinomio anziché un binomio. È quindi necessario utilizzare una formula diversa.

La formula per il quadrato della somma di 3 termini è la seguente:

$\definecolor{blauquadreejemplo}{HTML}{ff5733} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=blauquadreejemplo, boxrule=1.2pt, boxsep=2.5mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2.5mm}{-2.5mm}{0mm}{blauquadreejemplo!20!white,} ]}]{equation*} (a+b+c)^2 = a^2+2a(b+c)+b^2+2bc+c^2 \end{empheq}$

Vediamo come viene applicata questa formula attraverso un esempio:

$\begin{aligned} (2x+3y+5)^2 & = (2x)^2 + 2\cdot 2x (3y+5)+(3y)^2+2\cdot 3y \cdot 5 + 5^2 \\[2ex] & =4x^2 +4x (3y+5)+9y^2+30y +25 \\[2ex] &=4x^2 +12xy+20x+9y^2+30y +25 \end{aligned}$

Come puoi vedere, l’aggiunta di un elemento alla formula rende il risultato molto più complicato.

Qual è il quadrato di una somma?

Formula per il quadrato di una somma

Esempi di quadrati somma

Esempio 1

Esempio 2

Dimostrazione della formula del quadrato di una somma

Interpretazione geometrica del quadrato di una somma

Risolti problemi del quadrato di una somma

Esercizio 1

Esercizio 2

Esercizio 3

Quadrato di una somma di 3 termini

Lascia un commento Annulla risposta