Quadrato di una differenza (o sottrazione)

Qui spieghiamo qual è la formula di identità notevole del quadrato di una differenza (o sottrazione), cioè vi mostriamo come si risolve l’espressione (ab) ² . Inoltre, potrai vedere esempi ed esercitarti con esercizi risolti sul quadrato di una differenza. Infine, mostriamo la dimostrazione della formula e l’interpretazione geometrica di questo straordinario tipo di prodotto.

Qual è il quadrato di una differenza (o sottrazione)?

Il quadrato di una differenza , o quadrato di una sottrazione , è una delle identità notevoli (o prodotti notevoli), consiste cioè in una regola matematica che facilita il calcolo della quadratura di un binomio con due termini: uno positivo e l’altro negativo.

Pertanto, l’espressione algebrica del quadrato di una differenza è (ab) ² .

Formula per il quadrato di una differenza (o sottrazione)

Una volta vista la definizione di questo tipo di identità notevole, vedremo come risolvere il quadrato di una differenza con la sua formula:

Quindi il quadrato di una differenza è uguale al quadrato del primo termine, meno il doppio del prodotto del primo per il secondo, più il quadrato del secondo.

Quindi, per calcolare una differenza o una sottrazione al quadrato, non solo devi elevare ciascun termine a due, ma anche moltiplicarli insieme e per 2.

Questo è importante da ricordare, perché un errore molto comune quando si sottraggono i quadrati è non mettere il prodotto tra i due termini e risolvere solo il quadrato della diminuzione e la sottrazione della sottrazione:

Non dimenticare il prodotto tra a e b!

Esempi di quadrati di differenza (o sottrazione).

Ora che conosciamo la formula del quadrato di una differenza, possiamo utilizzarla per eseguire i calcoli. E affinché tu possa vedere come si fa, abbiamo preparato diversi esempi risolti del quadrato di una differenza (o sottrazione).

Esempio 1

Risolvi la seguente differenza al quadrato:

$(x-3)^2$

È una sottrazione al quadrato, quindi devi applicare la sua formula:

$(a-b)^2=a^2-2ab+b^2$

Quindi, dobbiamo identificare quali sono i valori delle incognite

$a$

$b$

della formula. In questo caso,

$a$

è la variabile

$x$

$b$

corrisponde al numero 3:

$\left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}$

Si noti che il segno negativo non ne fa parte

$b,$

ma devi sempre prendere il numero senza segno per applicare correttamente la formula.

Conosciamo quindi già i valori di

$a$

e di

$b$

Pertanto, dobbiamo solo sostituire questi valori nella formula:

binomio di un quadrato esercizi di sottrazione risolti

Esempio 2

Calcola il seguente binomio di una sottrazione al quadrato:

$(5x-2)^2$

La formula per la differenza al quadrato è:

$(a-b)^2=a^2-2ab+b^2$

Quindi, dobbiamo prima identificare i valori di

$a$

e di

$b$

della formula. In questo problema,

$a$

rappresenta il monomio

$5x$

$b$

è equivalente al termine indipendente del binomio, cioè 2:

$\left. \begin{array}{l} (a-b)^2\\[2ex] (5x-2)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=5x \\[2ex] b=2 \end{array}$

Infine, una volta conosciuto il valore dei parametri

$a$

$b$

, applichiamo semplicemente la formula binomiale per la sottrazione al quadrato:

$\begin{aligned} (5x-2)^2 & = (5x)^2-2\cdot 5x \cdot 2 + 2^2 \\[2ex] & = 25x^2-20x+4 \end{aligned}$

Dimostrazione della formula del quadrato di una differenza

Dedurremo quindi da dove viene la formula per il quadrato di una sottrazione. Anche se non è necessario memorizzare la dimostrazione, è comunque bello capirne i calcoli.

Se partiamo dall’espressione del binomio di ogni sottrazione:

$(a-b)^2$

Ovviamente la potenza precedente è uguale al prodotto del fattore

$(a-b)$

moltiplicato per se stesso:

$(a-b)^2= (a-b)\cdot (a-b)$

Ora moltiplichiamo le due parentesi applicando la proprietà distributiva:

$\begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}$

E non ci resta che raggruppare insieme termini simili per finire di dimostrare la formula:

$a^2-ab-ba+b^2 = a^2-2ab +b^2$

Affinché la formula del quadrato di una sottrazione sia dimostrata matematicamente:

$(a-b)^2=a^2-2ab+b^2$

Per curiosità, l’espansione dell’espressione binomiale di una sottrazione quadrata è anche nota come trinomio quadrato perfetto.

Interpretazione geometrica del quadrato di una differenza

Per finire di comprendere la nozione di quadrato di una differenza, vedremo come interpretare geometricamente questa notevole uguaglianza.

Osserva il seguente quadrato con i lati lunghi

$a:$

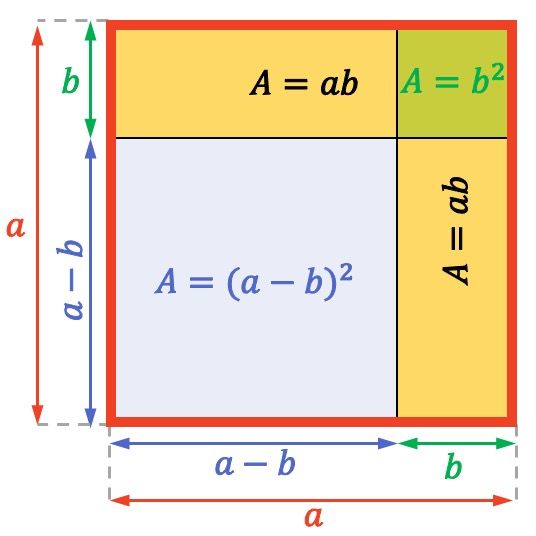
interpretazione geometrica del quadrato di una differenza

L’area (o superficie) di un quadrato o di un rettangolo si calcola moltiplicando due dei suoi lati adiacenti. Pertanto, l’area dell’intero quadrato intero sopra è

$a\cdot a = a^2.$

Allo stesso modo, l’area di ciascun rettangolo giallo è uguale a

$a\cdot b = ab.$

E infine, il quadratino mostrato in alto a destra ha un’area di

$b\cdot b =b^2.$

Ciò significa che un quadrato di lato

$(a-b),$

la cui superficie è

$(a-b)^2,$

può essere scomposto nell’area di un quadrato di dimensione

$a,$

meno 2 volte l’area di un rettangolo di dimensioni

$a$

$b$

, più l’area di un quadrato laterale

$b.$

In breve, la formula del quadrato di una differenza può essere verificata anche geometricamente:

$(a-b)^2=a^2-2ab+b^2$

Problemi risolti del quadrato di una differenza (o sottrazione)

Affinché tu possa esercitarti, ti lasciamo con diversi esercizi risolti passo dopo passo sul prodotto notevole del quadrato di una differenza. Ricorda che puoi scriverci qualsiasi domanda tu abbia qui sotto nei commenti.

Esercizio 1

Risolvi le seguenti sottrazioni al quadrato:

$\text{A)} \ (x-2)^2$

$\text{B)} \ (3-7x)^2$

$\text{C)} \ \left(x^2-6\right)^2$

$\text{D)} \ (-3x+y)^2$

$\text{E)} \ (4x-3y)^2$

vedi soluzione

Per trovare tutte le identità notevoli del problema è sufficiente applicare la formula del quadrato di una differenza, che è:

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}$

$\text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}$

$\text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}$

$\text{E)} \ \begin{aligned}(4x-3y)^2 & = (4x)^2-2\cdot 4x\cdot 3y +(3y)^2\\[2ex] & = \bm{16x^2-24xy+9y^2}\end{aligned}$

Esercizio 2

Determina i seguenti quadrati delle differenze di due quantità applicando la formula:

$\text{A)} \ \left(6x^3-4y^4\right)^2$

$\text{B)} \ \displaystyle \left(\sqrt{2x}-\sqrt{8x}\right)^2$

$\text{C)} \ \displaystyle \left(\frac{5}{2}x^2-\frac{4}{5}x\right)^2$

vedi soluzione

Per determinare tutti i prodotti notevoli del problema è necessario utilizzare la formula per la sottrazione al quadrato:

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2\\[2ex] & = \bm{36x^6-48x^3y^4+16y^8}\end{aligned}$

Per risolvere la sezione B), occorre ricordare che se una radice è quadrata si semplifica:

$\text{B)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}$

I monomi dell’ultima sottrazione quadrata hanno coefficienti frazionari, quindi per risolverla dobbiamo utilizzare le proprietà delle frazioni:

$\text{C)} \ \displaystyle \begin{aligned} \left(\frac{5}{2}x^2-\frac{4}{5}x\right)^2 & = \left(\frac{5}{2}x^2\right)^2-2\cdot \frac{5}{2}x^2\cdot \frac{4}{5}x +\left(\frac{4}{5}x\right)^2\\[2ex] & = \frac{5^2}{2^2}x^4-2\cdot \frac{20}{10}x^3 +\frac{4^2}{5^2}x^2 \\[2ex] &= \frac{25}{4}x^4 -2\cdot 2x^3+\frac{16}{25}x^2 \\[2ex] & = \mathbf{\frac{25}{4}} \bm{x^4-4x^3+}\mathbf{\frac{16}{25}}\bm{x^2}\end{aligned}$

Qual è il quadrato di una differenza (o sottrazione)?

Formula per il quadrato di una differenza (o sottrazione)

Esempi di quadrati di differenza (o sottrazione).

Esempio 1

Esempio 2

Dimostrazione della formula del quadrato di una differenza

Interpretazione geometrica del quadrato di una differenza

Problemi risolti del quadrato di una differenza (o sottrazione)

Esercizio 1

Esercizio 2

Lascia un commento Annulla risposta