Punto simmetrico rispetto ad un altro punto, ad una retta e ad un piano

Qui troverai come calcolare il punto di simmetria rispetto ad un altro punto, rispetto ad una retta e rispetto ad un piano. Inoltre, potrai vedere esempi ed esercizi risolti passo dopo passo.

Punto simmetrico rispetto ad un altro punto

Prima di vedere come viene calcolato il punto simmetrico, rivediamo cos’è esattamente un punto simmetrico rispetto a un altro punto:

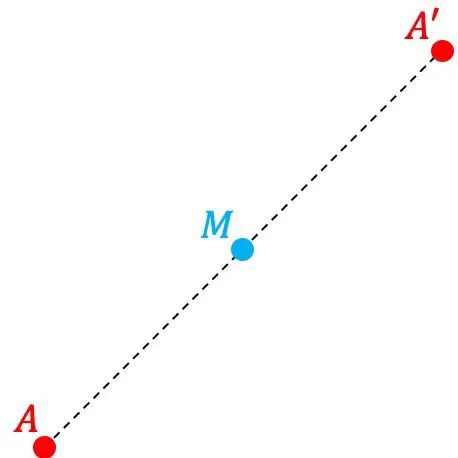
Il punto A’ è il punto simmetrico del punto A rispetto ad un altro punto M se il punto A’ si trova simmetricamente alla stessa distanza dal punto M della distanza tra i punti A e M. Pertanto, M è il punto medio del segmento formato da punti A e A’.

$d(A,M) = d(A',M )$

D’altra parte diciamo anche che il punto M è il centro di simmetria.

Quindi, per calcolare le coordinate del punto di simmetria, utilizzeremo la formula per il punto medio di un segmento :

$\cfrac{A+A'}{2}=M$

Da questa equazione estraiamo il punto incognito A’ e otteniamo la formula per il punto simmetrico rispetto ad un altro punto:

$\color{orange} \boxed{ \color{black} \quad A' = 2M - A \quad \vphantom{\Bigl)}}$

Esempio di ricerca del punto simmetrico rispetto ad un altro punto

Ad esempio calcoleremo il punto di simmetria del punto A rispetto al punto M. Consideriamo i due punti:

$A(1,3,0) \qquad \qquad M(-1,4,2)$

Per determinare il punto di simmetria tra questi due punti applichiamo la formula per il punto di simmetria rispetto ad un altro:

$A' = 2M - A$

Ora sostituiamo i punti nella formula:

$A' = 2(-1,4,2) -(1,3,0)$

E operiamo:

$A' = (-2,8,4) -(1,3,0)$

$\bm{A'=(-3,5,4)}$

punto simmetrico ad una retta

Abbiamo appena visto la nozione di punto simmetrico rispetto ad un altro punto. Ebbene, la simmetria di un punto rispetto ad una retta è molto simile:

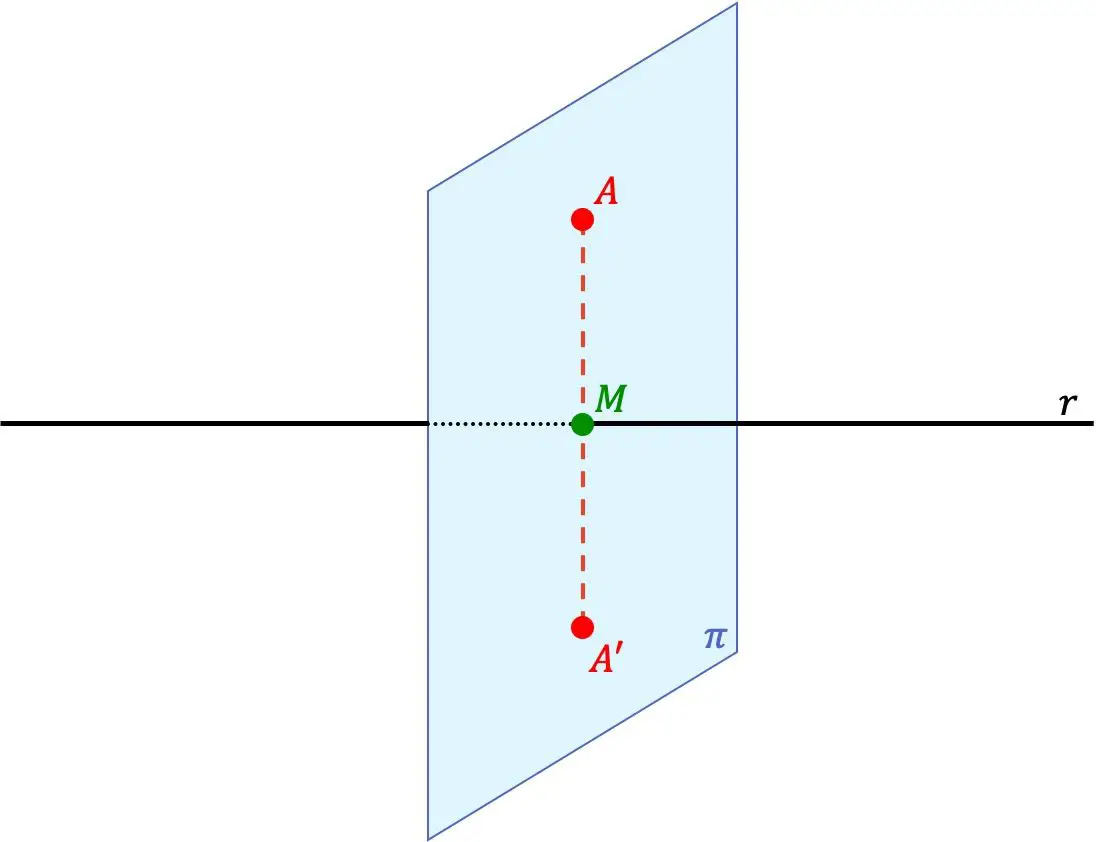
Il punto A’ è il punto simmetrico del punto A rispetto ad una retta se i due punti A’ e A giacciono sulla stessa retta perpendicolare alla retta e, inoltre, la distanza tra il punto A’ e la retta è pari alla distanza tra il punto A e la linea.

punto simmetrico di un punto rispetto ad una retta

$d(A,r)= d(A',r)$

Quindi anche la retta r è un asse di simmetria tra i punti.

Pertanto, per determinare il punto di simmetria del punto A rispetto alla retta r , dobbiamo seguire la seguente procedura:

Troviamo il piano perpendicolare alla linea r che passa per il punto A (piano π della precedente rappresentazione grafica). Per fare ciò dobbiamo utilizzare il vettore direzione della linea, che sarà il vettore normale del piano.
Calcoliamo il punto di intersezione tra il piano trovato e la linea (punto M nell’immagine precedente).
Usiamo la formula del punto simmetrico rispetto al punto (vista nella sezione precedente) per trovare il punto simmetrico del punto A rispetto al punto M. Il risultato è il punto simmetrico che stavamo cercando.

Esempio di calcolo del punto di simmetria rispetto ad una retta

Una volta saputo come calcolare il punto di simmetria di un altro punto rispetto ad una retta, vedremo risolto un esercizio come esempio:

Trovare il punto simmetrico del punto A rispetto alla retta r. Detto punto e linea:

$\displaystyle A(4,0,-1) \qquad \qquad r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases}$

Per prima cosa dobbiamo calcolare il piano perpendicolare alla linea r che passa per il punto A. Il vettore normale a questo piano sarà il vettore direzione della linea, le cui componenti sono i termini davanti al parametro

$t$

perché è espresso sotto forma di equazioni parametriche:

$\vv{n}=(1,4,-3)$

E i coefficienti A, B e C dell’equazione di un piano coincidono con le coordinate del suo vettore normale, quindi:

$\vv{n}=(1,4,-3) \quad \longrightarrow \quad \pi : \ 1x+4y-3z+D=0$

Il punto A deve giacere su questo piano, quindi ora possiamo sostituire il punto A nell’equazione del piano per trovare il coefficiente D:

$A(4,0,-1)$

$4+4\cdot 0-3\cdot (-1)+D=0$

$4+3+D=0$

$7+D=0$

$D=-7$

Pertanto l’equazione del piano perpendicolare alla retta ry passante per il punto A è:

$\pi : \ x+4y-3z-7=0$

Una volta conosciuta l’equazione del piano, dobbiamo calcolare il punto di intersezione tra il piano e la retta. Per fare ciò, sostituiamo le coordinate della retta nell’equazione del piano e risolviamo l’equazione risultante:

$\displaystyle r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases} \qquad \qquad \pi : \ x+4y-3z-7=0$

$(1+t)+4(5+4t)-3(-4-3t)-7=0$

$1+t+20+16t+12+9t-7=0$

$26t+26=0$

$26t=-26$

$t=\cfrac{-26}{26}$

$t=-1$

Ora sostituiamo il valore di

$t$

ottenuto nell’equazione della retta:

$\displaystyle t=-1 \ \longrightarrow \ \begin{cases}x=1 -1=0 \\[1.7ex] y=5 +4\cdot (-1)=1\\[1.7ex] z=-4-3\cdot (-1)=-1 \end{cases}$

Quindi il punto di intersezione tra la retta r ed il piano ad essa perpendicolare è:

$M(0,1,-1)$

Infine è sufficiente trovare il punto simmetrico del punto A rispetto al punto M; per questo possiamo utilizzare la formula vista all’inizio di questa pagina:

$\begin{aligned} A' & = 2M - A \\[2ex] &= 2(0,1,-1) - (4,0,-1) \\[2ex] & = (0,2,-2)-(4,0,-1)\\[2ex] & = \bm{(-4,2,-1)} \end{aligned}$

punto simmetrico ad un piano

Prima di vedere il metodo per determinare il punto di simmetria di un altro punto rispetto ad un piano, vediamo qual è la sua definizione:

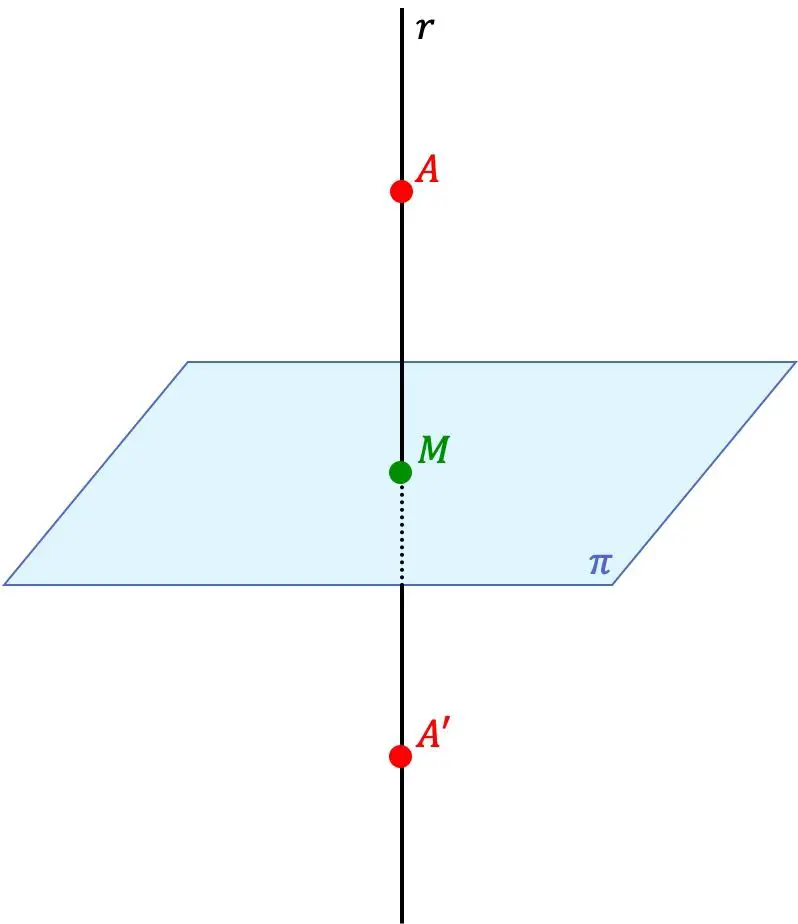
Il punto A’ è il punto simmetrico del punto A rispetto ad un piano se i due punti A’ e A giacciono sulla stessa retta perpendicolare al piano e, inoltre, la distanza tra il punto A’ e il piano è equivalente alla distanza tra il punto A e il piano.

punto simmetrico ad un altro punto rispetto ad un piano

$d(A,\pi)= d(A',\pi)$

Quindi il piano è anche un piano di simmetria tra i due punti.

Pertanto, per conoscere le coordinate cartesiane del punto simmetrico del punto A rispetto al piano π, è necessario seguire i seguenti passi:

Troviamo l’equazione della retta perpendicolare al piano che passa per il punto A. Per questo utilizzeremo il vettore normale al piano come vettore di direzione della retta.
Calcoliamo il punto di intersezione tra il piano e la linea trovata (punto M dell’immagine precedente).
Usiamo la formula del punto simmetrico rispetto al punto (vista nella sezione iniziale) per trovare il punto simmetrico del punto A rispetto al punto M. Il risultato è il punto simmetrico che stavamo cercando.

Esempio di determinazione del punto di simmetria rispetto ad un piano

Di seguito potete vedere un problema risolto riguardante il punto di simmetria di un altro punto rispetto ad un piano:

Determinare il punto di simmetria di A rispetto al piano π. Detto punto e piano:

$\displaystyle A(3,-4,2) \qquad \qquad \pi: \ 2x+y-z-6=0$

La prima cosa che dobbiamo fare è trovare l’equazione della retta perpendicolare al piano e che passa per il punto A. Per fare ciò possiamo usare come vettore direzione della retta il vettore normale al piano, le cui componenti X, Y, Z sono i coefficienti rispettivamente dei termini A, B e C dell’equazione del piano:

$\pi: \ 2x+y-z-6=0 \quad \longrightarrow \quad \vv{n} = (2,1,-1)$

Possiamo ora costruire le equazioni parametriche della retta ortogonale al piano con il vettore direzione trovato e un suo punto (punto A):

$\displaystyle r: \ \begin{cases}x=3 + 2t \\[1.7ex] y=-4 +t\\[1.7ex] z=2-t \end{cases}$

Una volta conosciuta la retta perpendicolare, calcoliamo il punto di intersezione del piano e della retta sostituendo le coordinate della retta nell’equazione del piano:

$\displaystyle r: \ \begin{cases}x=3 + 2t \\[1.7ex] y=-4 +t\\[1.7ex] z=2-t \end{cases} \qquad \qquad \pi : \ 2x+y-z-6=0$

$2(3+2t)+(-4+t)-(2-t)-6=0$

$6+4t-4+t-2+t-6=0$

$6t-6=0$

$6t=6$

$t=\cfrac{6}{6}$

$t=1$

Ora sostituiamo il valore di

$t$

ottenuto nell’equazione della retta:

$\displaystyle t=1 \ \longrightarrow \ \begin{cases}x=3 + 2\cdot 1 =5\\[1.7ex] y=-4 +1=-3\\[1.7ex] z=2-1=1 \end{cases}$

Quindi il punto di intersezione tra il piano e la retta perpendicolare è:

$M(5,-3,1)$

Infine, non ci resta che trovare il punto simmetrico del punto A rispetto al punto M. E, per farlo, possiamo utilizzare la formula vista all’inizio di questa pagina:

$\begin{aligned} A' & = 2M - A \\[2ex] &= 2(5,-3,1) - (3,-4,2) \\[2ex] & = (10,-6,2)-(3,-4,2)\\[2ex] & = \bm{(7,-2,0)} \end{aligned}$

Punto simmetrico rispetto ad un altro punto, una retta e un piano