Come calcolare i punti di taglio di una funzione con gli assi

In questa pagina viene spiegato quali sono i punti di intersezione (o incrocio) di una funzione con gli assi cartesiani e come calcolarli. Inoltre, troverai diversi esempi per comprendere appieno come si trovano e potrai anche esercitarti con esercizi risolti passo dopo passo.

Quali sono i punti di intersezione (o intersezione) di una funzione con gli assi?

Prima di vedere come si calcolano, ricordiamo quali sono i punti di intersezione di una funzione con gli assi.

I punti di intersezione o di intersezione degli assi sono i punti in cui la rappresentazione di una funzione interseca gli assi delle coordinate, cioè i punti del grafico che si lega sull’asse X e sull’asse l. Asse Y.

Ad esempio, la parabola nel grafico seguente interseca l’asse Y nel punto (0,3) e interseca l’asse X nei punti (-1,0) e (3,0).

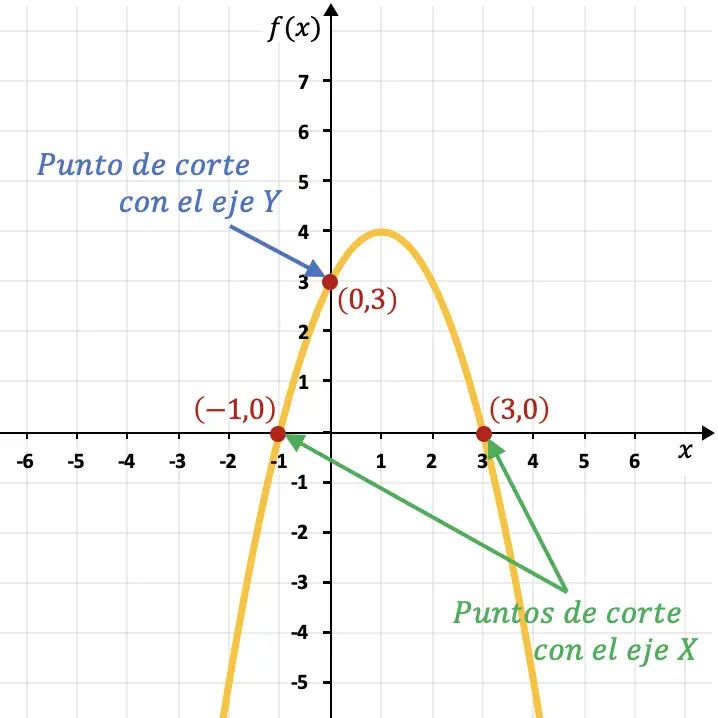
Punti di taglio o di intersezione di una funzione con gli assi

Punto di taglio di una funzione con l’asse X

La seconda coordinata dei punti di intersezione di una funzione con l’asse X sarà sempre 0, quindi:

I punti limite di qualsiasi funzione dell’asse x OX sono nella forma

$(a,0)$

, e può essere calcolato risolvendo la seguente equazione:

$f(x)=0$

A volte quando risolviamo questa equazione possiamo ottenere due (o più) soluzioni, ciò significa che la funzione interseca l’asse X due (o più) volte. D’altra parte, se l’equazione non ha soluzione, ciò implica che la funzione non interseca l’asse X.

Punto di taglio di una funzione con l’asse Y

La prima coordinata dei punti di intersezione di una funzione con l’asse Y sarà sempre 0, quindi:

Il punto limite di qualsiasi funzione con l’asse y OY è nella forma

$(0,a)$

, e può essere trovato calcolando l’immagine della funzione in x=0:

$f(0)$

A differenza dei punti di interruzione sull’asse X, può esserci un solo punto di interruzione sull’asse Y.

Esempio di calcolo dei punti limite di una funzione con gli assi

Per non avere dubbi, vedremo di seguito un esempio di come trovare i punti di taglio di una funzione con gli assi cartesiani:

Trova numericamente i punti limite della seguente funzione:

$f(x)=-2x+4$

Per prima cosa calcoleremo il punto limite della funzione con l’asse x. Il punto di intersezione con l’asse X avrà sempre la seconda componente pari a 0, cioè sarà del tipo

$(a,0)$

. Perché f(x) è sempre uguale a 0 sull’asse OX. Quindi per trovare l’altra componente del punto dobbiamo risolvere l’equazione

$f(x)=0:$

$f(x)=0$

$-2x+4=0$

$-2x=-4$

$x=\cfrac{-4}{-2}=2$

Il punto di intersezione con l’asse X è quindi:

$\bm{(2,0)}$

Ora troveremo il punto di intersezione con l’asse y. Il punto di intersezione con l’asse Y avrà sempre la prima componente pari a 0, cioè il punto sarà del tipo

$(0,a)$

. Poiché la variabile indipendente x si annulla sempre sull’asse Y. Quindi per trovare l’altra coordinata del punto dobbiamo calcolare

$f(0):$

$f(0)=-2 \cdot 0+4=4$

Il punto di intersezione con l’asse Y è quindi:

$\bm{(0,4)}$

Di seguito avete rappresentata graficamente la funzione di esempio, potete vedere che le soglie trovate coincidono con quelle del grafico:

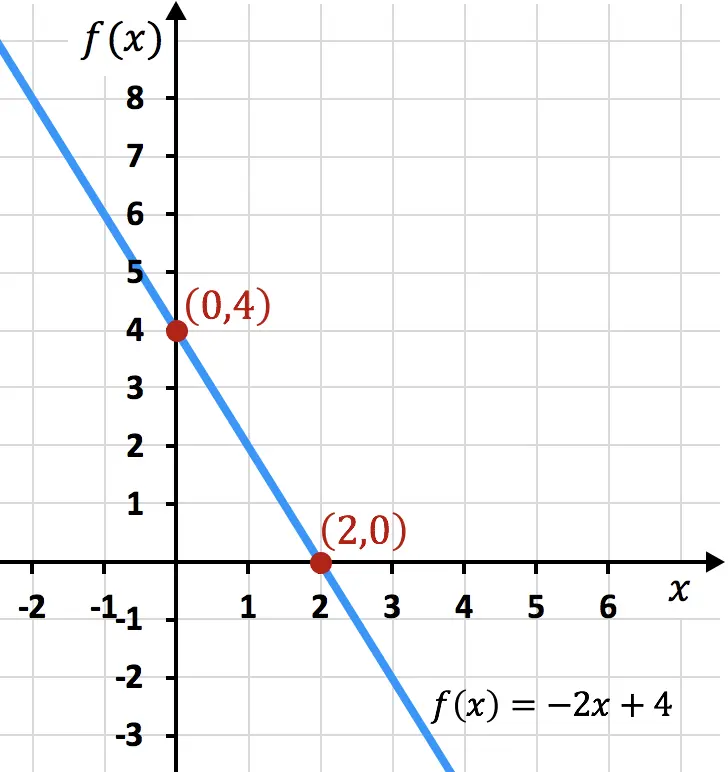
come trovare i punti di taglio di una funzione con assi

Esercizi risolti per i punti di taglio di una funzione con assi

Esercizio 1

Determinare i punti di taglio con gli assi delle coordinate della seguente funzione:

$f(x)=3x-3$

Vedi la soluzione

Punto di taglio con asse X

Per trovare il punto di intersezione della funzione con l’asse X è necessario risolvere

$f(x)=0:$

$f(x)=0$

$3x-3=0$

$3x=3$

$x=\cfrac{3}{3}=1$

Il punto di intersezione della funzione con l’asse X è quindi:

$\bm{(1,0)}$

Punto di taglio con asse Y

Per trovare il punto di intersezione con l’asse Y devi calcolare

$f(0):$

$f(0)=3\cdot 0 -3= -3$

Il punto di intersezione della funzione con l’asse Y è quindi:

$\bm{(0,-3)}$

Esercizio 2

Trovare i punti di intersezione con gli assi cartesiani della seguente funzione affine:

$f(x)=2x+8$

Vedi la soluzione

Punto di taglio con asse X

Per trovare il punto limite della funzione con l’asse OX, dobbiamo porre la funzione uguale a zero e risolvere l’equazione risultante:

$f(x)=0$

$2x+8=0$

$2x=-8$

$x=\cfrac{-8}{2}=-4$

Quindi il punto di intersezione della funzione con l’asse delle ascisse è:

$\bm{(-4,0)}$

Punto di taglio con asse Y

Per trovare il punto di interruzione con l’asse OY, dobbiamo calcolare

$f(0):$

$f(0)=2\cdot 0 +8= 8$

Il punto di intersezione della funzione con l’asse del computer è quindi:

$\bm{(0,8)}$

Esercizio 3

Calcolare i punti limite con gli assi della seguente funzione quadratica:

$f(x)=x^2-3x+2$

Vedi la soluzione

Punto di taglio con asse X

Per trovare il punto di intersezione della funzione con l’asse X è necessario risolvere

$f(x)=0:$

$f(x)=0$

$x^2-3x+2=0$

In questo caso, dobbiamo risolvere un’equazione quadratica, quindi applichiamo la formula:

$\displaystyle x =\cfrac{-b \pm \sqrt{b^2 -4ac}}{2a}$

$\displaystyle x=\cfrac{ -(-3) \pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2\cdot 1} = \cfrac{3 \pm 1}{2} = \begin{cases} 2 \\[2ex] 1 \end{cases}$

Abbiamo ottenuto due soluzioni dell’equazione quadratica, quindi la funzione interseca l’asse X in due punti:

$\bm{(1,0)} \qquad \bm{(2,0)}$

Punto di taglio con asse Y

Per determinare invece il punto di intersezione con l’asse Y è necessario calcolare

$f(0):$

$f(0)=0^2-3\cdot 0+2= 2$

Pertanto l’unico punto di intersezione della funzione con l’asse Y è:

$\bm{(0,2)}$

Esercizio 4

Trovare i punti di intersezione con gli assi del piano cartesiano della seguente funzione razionale:

$f(x)=\cfrac{5}{x}$

Vedi la soluzione

Punto di taglio con asse X

Per trovare il punto di intersezione della funzione con l’asse X è necessario risolvere

$f(x)=0:$

$f(x)=0$

$\cfrac{5}{x}=0$

$5=0\cdot x$

$5=0$

$5\neq 0$

5 non equivale a 0, quindi l’equazione non ha soluzione e, quindi, non esiste alcun punto di intersezione tra la funzione e l’asse X.

Punto di taglio con asse Y

Per trovare il punto di intersezione con l’asse Y devi calcolare

$f(0):$

$f(0)=\cfrac{5}{0}= \infty$

Qualsiasi numero diviso per zero è un’indeterminazione che dà infinito. Pertanto, la funzione non si estende oltre l’asse Y in nessun punto.

In breve, la funzione di esercizio non ha punti di intersezione con gli assi , cioè il suo grafico non passa né per l’asse X né per l’asse Y in nessun punto.

Esercizio 5

Calcolare i punti limite con gli assi della seguente funzione di terzo grado:

$f(x)=x^3-9x$

Vedi la soluzione

Punto di taglio con asse X

Per trovare il punto di intersezione della funzione con l’asse X è necessario risolvere

$f(x)=0:$

$f(x)=0$

$x^3-9x=0$

Entrambi i termini dell’equazione hanno una x , con la quale possiamo estrarre un fattore comune:

$x(x^2-9)=0$

Affinché l’uguaglianza precedente sia soddisfatta, uno dei fattori deve essere 0. Pertanto, poniamo ciascun fattore uguale a zero per ottenere tutte le soluzioni possibili:

$\displaystyle x(x^2-9)=0 \ \longrightarrow \begin{cases} \bm{x = 0} \\[2ex] x^2-9 = 0\ \longrightarrow \ x^2=9 \ \longrightarrow \ \bm{x=\pm 3} \end{cases}$

Abbiamo quindi ottenuto tre soluzioni dell’equazione di terzo grado, quindi la funzione taglia l’asse X in 3 punti:

$\bm{(-3,0)} \qquad \bm{(0,0)} \qquad \bm{(3,0)}$

Punto di taglio con asse Y

Per calcolare il punto di taglio con l’asse Y, è necessario calcolare

$f(0):$

$f(0)=0^3-9\cdot 0 = 0$

Pertanto, l’unico punto di intersezione della funzione con l’asse Y è l’origine delle coordinate (0,0):

$\bm{(0,0)}$

Si noti che questo punto lo avevamo già trovato nel calcolo del punto di taglio con l’asse X, perché la funzione taglia in questo punto con entrambi gli assi contemporaneamente.

Quali sono i punti di intersezione (o intersezione) di una funzione con gli assi?

Punto di taglio di una funzione con l’asse X

Punto di taglio di una funzione con l’asse Y

Esempio di calcolo dei punti limite di una funzione con gli assi

Esercizi risolti per i punti di taglio di una funzione con assi

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Lascia un commento Annulla risposta