Punti di flesso di una funzione -

Qui spieghiamo cos’è un punto di flesso di una funzione e come trovare tutti i punti di flesso di una funzione. Inoltre, troverai esercizi passo passo sulla curvatura e sui punti di flesso di una funzione.

Quali sono i punti di flesso di una funzione?

I punti di flesso di una funzione sono i punti in cui il grafico della funzione cambia curvatura, cioè in un punto di flesso una funzione cambia da concava a convessa o viceversa.

Come sapere se una funzione ha un punto di flesso

Data la definizione di punto di flesso, vediamo come sapere se un certo punto è un punto di flesso della funzione.

Una funzione ha un punto di flesso nei punti che annullano la sua derivata seconda e la sua derivata terza è diversa da zero.

$\left.\begin{array}{l}f''(a)=0\\[2ex]f'''(a)\neq 0\end{array}\right\} \quad \bm{\longrightarrow} \quad x=a \text{ es un punto de inflexi\'on}$

Ad esempio, calcoleremo i punti di flesso della seguente funzione di terzo grado:

$f(x)=x^3-5x$

Per prima cosa calcoliamo la derivata seconda e terza della funzione:

$f'(x)=3x^2-5$

$f''(x)=6x$

$f'''(x)=6$

Ora impostiamo la derivata seconda uguale a 0 e risolviamo l’equazione risultante:

$6x=0$

$x=0$

Quindi, il punto x=0 sarà un punto di flesso della funzione se la derivata terza è diversa da zero in questo punto. Nel nostro caso la derivata terza è sempre uguale a 6.

$f'''(0)=6\neq 0$

Pertanto, x=0 è un punto di flesso della funzione.

Come studiare la curvatura e trovare i punti di flesso di una funzione

Abbiamo appena visto un metodo per trovare punti di svolta. Tuttavia, normalmente tendiamo a studiare la curvatura di una funzione, cioè a determinare la concavità e la convessità di una funzione, e da lì a calcolare i punti di flesso.

Per trovare i punti di flesso di una funzione attraverso la sua curvatura, è necessario eseguire i seguenti passaggi:

Trova i punti che non appartengono al dominio della funzione.
Calcolare la derivata prima e la derivata seconda della funzione.
Trova le radici della derivata seconda , cioè calcola i punti che annullano la derivata seconda risolvendo
$f''(x)=0$

.
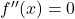
Crea intervalli con le radici della derivata e i punti che non appartengono al dominio della funzione.
Calcola il valore della derivata seconda in un punto di ciascun intervallo.
Il segno della derivata seconda determina la concavità o convessità della funzione in questo intervallo:
- Se la derivata seconda della funzione è positiva, la funzione è convessa su questo intervallo.
- Se la derivata seconda della funzione è negativa, la funzione è concava su questo intervallo.
I punti di flesso sono i punti in cui la funzione cambia da convessa a concava o viceversa.

Affinché tu possa vedere come vengono calcolati i punti di flesso di una funzione utilizzando questa procedura, risolveremo un esempio passo dopo passo di seguito:

Studia la curvatura e trova i punti di flesso della seguente funzione polinomiale:

$f(x)=x^4-6x^2$

La prima cosa da fare è calcolare il dominio di definizione della funzione. È una funzione polinomiale, quindi il dominio della funzione è costituito da numeri reali, cioè è una funzione continua:

$\text{Dom } f= \mathbb{R}$

Una volta calcolato il dominio della funzione, dobbiamo studiare in quali punti si realizza

$f''(x)=0$

Calcoliamo quindi prima la derivata prima della funzione:

$f(x)=x^4-6x^2 \ \longrightarrow \ f'(x)= 4x^3-12x$

Successivamente calcoliamo la derivata seconda della funzione:

$f'(x)=4x^3-12x \ \longrightarrow \ f''(x)= 12x^2-12$

E ora impostiamo la derivata seconda uguale a 0 e risolviamo l’equazione:

$f''(x)=0$

$12x^2-12=0$

$12x^2=12$

$x^2=\cfrac{12}{12}$

$x^2=1$

$\sqrt{x^2}=\sqrt{1}$

$x=\pm1$

Una volta calcolato il dominio della funzione e

$f''(x)=0$

, rappresentiamo tutti i punti critici che si trovano sulla retta numerica:

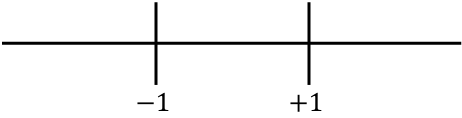
E ora valutiamo il segno della derivata seconda in ogni intervallo, per sapere se la funzione è concava o convessa. Prendiamo quindi un punto in ogni intervallo (mai i punti critici) e guardiamo che segno ha la derivata seconda in questo punto:

$f''(x)=12x^2-12$

$f''(-2) = 12\cdot (-2)^2-12 =36 \ \rightarrow \ \bm{+}$

$f''(0) = 12\cdot 0^2-12 = -12 \ \rightarrow \ \bm{-}$

$f''(2) = 12\cdot 2^2-12=36 \ \rightarrow \ \bm{+}$

Se la derivata seconda è positiva significa che la funzione è convessa.

$(\bm{\cup})$

, e se la derivata seconda è negativa significa che la funzione è concava

$(\bm{\cap})$

. Pertanto, gli intervalli di concavità e convessità della funzione sono:

Convesso

$(\bm{\cup})$

$\bm{(-\infty,-1) \cup (1,+\infty)}$

Concavo

$(\bm{\cap})$

$\bm{(-1,1)}$

Inoltre, in x=-1 la funzione passa da convessa a concava, quindi x=-1 è un punto di flesso della funzione . E in x=1, la funzione passa da concava a convessa, quindi x=1 è anche un punto di flesso della funzione.

Infine, sostituiamo i punti trovati nella funzione originale per trovare la coordinata Y dei punti di flesso:

$f(-1)=(-1)^4-6(-1)^2 = 1-6 \cdot 1 = -5 \ \longrightarrow \ (-1,-5)$

$f(1)=1^4-6\cdot 1^2 = 1-6 \cdot 1 = -5 \ \longrightarrow \ (1,-5)$

I punti di svolta della funzione sono quindi:

Punti di svolta:

$\bm{(-1,-5)}$

$\bm{(1,-5)}$

Di seguito potete vedere la rappresentazione grafica della funzione studiata:

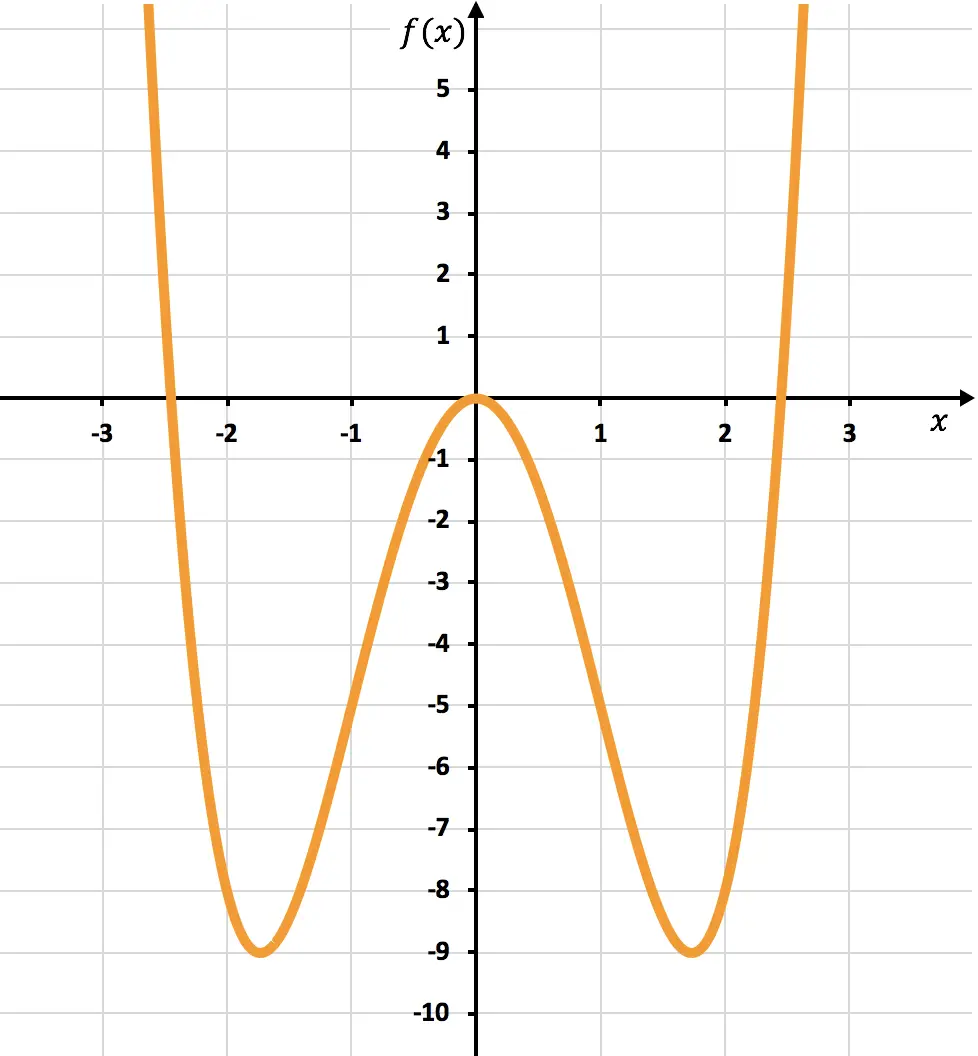
Come puoi vedere dal grafico, la funzione va da convessa

$(\cup)$

essere concavo

$(\cap)$

$(-1,-5)$

poiché la sua curvatura cambia. E d’altra parte la funzione va da concava

$(\cap)$

essere convesso

$(\cup)$

$(1,-5)$

Esercizi di svolta risolti

Esercizio 1

Calcola gli intervalli di concavità e convessità nonché i punti di flesso della seguente funzione esponenziale:

$f(x) = xe^x$

Vedi la soluzione

La prima cosa da fare è calcolare il dominio di definizione della funzione. La funzione è composta da una funzione polinomiale (x), il cui dominio è costituito solo da numeri reali, e da una funzione esponenziale (e ^x ), il cui dominio è costituito anch’esso da numeri reali. Pertanto, il dominio della funzione è costituito da numeri reali:

$\text{Dom } f= \mathbb{R}$

Ora calcoliamo la derivata della funzione. In questo caso la funzione è composta dal prodotto di due funzioni, quindi per derivare la funzione dobbiamo applicare la formula per la derivata di un prodotto:

$f'(x)=1 \cdot e^x+ x \cdot e^x$

$f'(x)=e^x +xe^x$

Successivamente calcoliamo la derivata seconda della funzione:

$f''(x)= e^x + 1 \cdot e^x+ x \cdot e^x$

$f''(x)=e^x +e^x + xe^x = 2e^x +xe^x$

Impostiamo la derivata seconda uguale a 0 e risolviamo l’equazione:

$f''(x)= 0$

$2e^x+xe^x= 0$

Estraiamo il fattore comune:

$e^x(2+x)=0$

Perché la moltiplicazione sia uguale a 0, uno dei due elementi della moltiplicazione deve essere zero. Pertanto, impostiamo ciascun fattore uguale a 0:

$\displaystyle e^x\cdot(2+x) =0 \longrightarrow \begin{cases} e^x=0 \ \color{red}\bm{\times}\color{black} \\[2ex] 2+x=0 \ \longrightarrow \ x= - 2 \end{cases}$

Un numero elevato a un altro non può mai dare come risultato 0. Pertanto, l’equazione

$e^x=0$

Non c’è soluzione.

Rappresentiamo tutti i punti singolari ottenuti a destra:

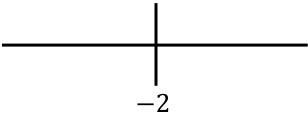
E ora valutiamo il segno della derivata seconda in ciascun intervallo per sapere se la funzione è concava o convessa. Per fare ciò, prendiamo un punto in ciascun intervallo e guardiamo quale segno ha la derivata seconda in quel punto:

$f''(-3)= 2e^{-3} +(-3)\cdot e^{-3} = 0,1 - 0,15 = -0,05\ \rightarrow \ \bm{-}$

$f''(0)= 2e^0 +0\cdot e^0 = 2 \cdot 1 + 0 \cdot 1 =2+0= 2 \ \rightarrow \ \bm{+}$

Se la derivata seconda è positiva significa che la funzione è convessa.

$(\bm{\cup})$

, e se la derivata seconda è negativa significa che la funzione è concava

$(\bm{\cap})$

. Gli intervalli di concavità e convessità sono quindi:

Convesso

$(\bm{\cup})$

$\bm{(-2,+\infty)}$

Concavo

$(\bm{\cap})$

$\bm{(-\infty,-2)}$

Inoltre, la funzione cambia da concava a convessa in x=-2, quindi x=-2 è un punto di flesso della funzione.

Infine, sostituiamo il punto di flesso trovato nella funzione originale per trovare la coordinata Y del punto:

$f(-2) = (-2)\cdot e^{-2} =-2e^{-2} \ \longrightarrow \ (-2,-2e^{-2})$

In conclusione gli unici punti di svolta della funzione sono:

Punti di svolta:

$\bm{(-2,-2e^{-2})}$

Esercizio 2

Studia gli intervalli di concavità e convessità e trova i punti di flesso della seguente funzione razionale:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Vedi la soluzione

Per prima cosa dobbiamo calcolare il dominio della funzione. Trattandosi di una funzione razionale, poniamo il denominatore uguale a zero per vedere quali numeri non appartengono al dominio della funzione:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

Ciò significa che quando x è -2 o +2, il denominatore sarà 0. E quindi la funzione non esisterà. Il dominio della funzione è quindi composto da tutti i numeri tranne x=-2 e x=+2.

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

In secondo luogo, calcoliamo la derivata prima della funzione:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

E poi risolviamo la derivata seconda:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

Tutti i termini vengono moltiplicati per

$(x^2-4)$

. Possiamo quindi semplificare la frazione:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Ora calcoliamo le radici della derivata seconda della funzione:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

Il termine

$\left(x^2-4\right)^3$

Ciò comporta la divisione dell’intero lato sinistro, quindi possiamo moltiplicarlo per l’intero lato destro:

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

Estraiamo il fattore comune:

$x(8x^2+96)=0$

Perché la moltiplicazione sia uguale a 0, uno dei due elementi della moltiplicazione deve essere zero. Pertanto, impostiamo ciascun fattore uguale a 0:

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

Non esiste una soluzione poiché non esiste una radice negativa di un numero reale.

Rappresentiamo ora sulla retta tutti i punti critici ottenuti, cioè i punti che non appartengono al dominio (x=-2 e x=+2) e quelli che annullano la derivata seconda (x=0):

E valutiamo il segno della derivata seconda in ogni intervallo, per sapere se la funzione è concava o convessa. Quindi prendiamo un punto in ogni intervallo e guardiamo quale segno ha la derivata seconda in quel punto:

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

Se la derivata seconda è positiva significa che la funzione è convessa.

$(\bm{\cup})$

, e se la derivata seconda è negativa significa che la funzione è concava

$(\bm{\cap})$

. Gli intervalli di concavità e convessità sono quindi:

Convesso

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

Concavo

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

La funzione cambia curvatura in tre punti, quindi la funzione razionale avrebbe in linea di principio tre punti di flesso, che sono x=-2, x=0 e x=2. Tuttavia, sebbene vi sia un cambiamento nella curvatura in x=-2 e in x=+2, questi non sono punti di flesso perché non appartengono al dominio della funzione. D’altra parte, in x=0 c’è un cambiamento nella curvatura e questo appartiene alla funzione, quindi x=0 è l’unico punto di flesso della funzione.

Non resta che calcolare la coordinata Y del punto di flesso:

$\displaystyle f(0)=\frac{0^3}{0^2-4} =\frac{0}{-4}=0\ \longrightarrow \ (0,0)$

In breve, l’unico punto di flesso della funzione razionale è l’origine delle coordinate:

Punti di svolta:

$\bm{(0,0)}$

Esercizio 3

Sappiamo che la funzione

$f(x)=x^3+ax^2+bx+c$

passare per il punto

$(3,1)$

, ha un estremo relativo in

$x=1$

e una svolta decisiva

$x = 2$

. Da queste informazioni, calcolare i valori dei parametri

$a, b$

$c$

Vedi la soluzione

Lascia che la funzione abbia un punto di flesso in

$x= 2$

significa che

$f''(2)=0$

. Pertanto, calcoliamo la derivata seconda della funzione in

$x= 2$

e lo impostiamo uguale a 0:

$f(x) = x^3+ax^2+bx+c \ \longrightarrow \ f'(x)=3x^2+2ax+b$

$f'(x)=3x^2+2ax+b \ \longrightarrow \ f''(x)= 6x+2a$

$\left. \begin{array}{l} f''(2)=6\cdot 2+2a\\[2ex] f''(2)=0\end{array} \right\} \longrightarrow 6\cdot 2+2a=0$

E risolviamo l’equazione ottenuta per trovare il valore del parametro a:

$6\cdot 2+2a=0$

$12+2a=0$

$2a=-12$

$a=\cfrac{-12}{2}$

$\bm{a=-6}$

La funzione sarà quindi:

$f(x)=x^3+ax^2+bx+c \ \xrightarrow{a \ = \ -6}\ f(x)=x^3-6x^2+bx+c$

Inoltre, la funzione ha un estremo in

$x= 1$

, Che significa che

$f'(1)=0$

. Pertanto, calcoliamo la derivata prima della funzione in

$x= 1$

e lo impostiamo uguale a 0:

$f(x)=x^3-6x^2+bx+c \ \longrightarrow \ f'(x)=3x^2-12x+b$

$\left. \begin{array}{l} f'(1)=3\cdot 1^2-12\cdot 1+b\\[2ex] f'(1)=0\end{array} \right\} \longrightarrow 3\cdot 1^2-12\cdot 1+b=0$

E risolviamo l’equazione ottenuta per trovare il valore dell’incognita b:

$3\cdot 1^2-12\cdot 1+b=0$

$3 \cdot 1 -12 + b = 0$

$3 -12 + b = 0$

$b=+12-3$

$\bm{b=9}$

La funzione sarà quindi:

$f(x)=x^3-6x^2+bx+c \ \xrightarrow{b \ = \ 9} \ f(x)=x^3-6x^2+9x+c$

Ci dicono invece che la funzione passa per il punto (3,1). Questo è da dire,

$f(3)=1$

. Pertanto, possiamo applicare questa condizione per trovare il valore del parametro c:

$\left. \begin{array}{l} f(3)=3^3-6\cdot 3^2+9\cdot3+c \\[2ex] f(3)=1 \end{array} \right\} \longrightarrow 3^3-6\cdot 3^2+9\cdot 3+c = 1$

E risolviamo l’equazione ottenuta per trovare il valore di

$b:$

$3^3-6\cdot 3^2+9\cdot 3+c = 1$

$27-6\cdot 9+27+c = 1$

$27-54+27+c = 1$

$c=1-27+54-27$

$\bm{c=1}$

La funzione sarà quindi:

$f(x)=x^3-6x^2+9x+c \ \xrightarrow{c \ = \ 1} \ f(x)=x^3-6x^2+9x+1$

Quali sono i punti di flesso di una funzione?

Come sapere se una funzione ha un punto di flesso

Come studiare la curvatura e trovare i punti di flesso di una funzione

Esercizi di svolta risolti

Esercizio 1

Esercizio 2

Esercizio 3

Lascia un commento Annulla risposta