▷ Cos'è e come viene calcolato un numero combinatorio (esempi)

In questa pagina spieghiamo cos’è un numero combinatorio e come si calcola (formula). Inoltre, potrai vedere esempi di come calcolare qualsiasi numero combinatorio ed esercitarti con esercizi risolti passo dopo passo. Mostriamo anche tutte le proprietà e le applicazioni dei numeri combinatori. E infine, impariamo a trovare il risultato di un numero combinatorio direttamente con la calcolatrice.

Cos’è un numero combinatorio?

In matematica il numero combinatorio , detto anche coefficiente binomiale, è il numero di combinazioni ordinarie (combinazioni senza ripetizione) di gruppi di k elementi che si possono formare da un insieme di n elementi (n>k).

Un numero combinatorio è espresso tra parentesi come segue:

$\begin{pmatrix}n \\ k \end{pmatrix}$

D’altra parte, il numero combinatorio viene letto n su k . Allo stesso modo, n è chiamato numeratore e k è chiamato ordine.

Proprio con la definizione di numero combinatorio è difficile comprenderne il significato. Tuttavia, vedremo ora come viene determinato matematicamente il numero combinatorio, e poi approfondiremo questo concetto di combinatoria. Vedrai che così lo capirai meglio.

Formula dei numeri combinatori

La formula per calcolare il valore di un numero combinatorio (o coefficiente binomiale) è la seguente:

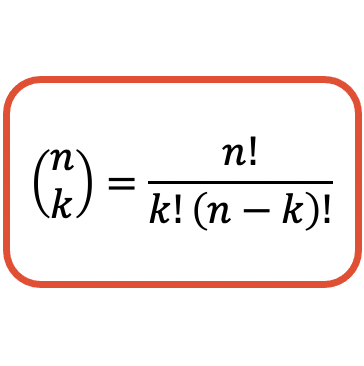
Ricorda che in algebra il punto esclamativo corrisponde al fattoriale di un numero. E per trovare il fattoriale di un numero, devi moltiplicare tutti i numeri interi positivi di 1 per quel numero. Ad esempio, per calcolare il fattoriale del numero 4 devi moltiplicare 1, 2, 3 e 4:

$4! = 1\cdot 2 \cdot 3 \cdot 4 =24$

È anche importante sapere che il fattoriale di 0 è uguale a 1.

$0! = 1$

Esempio di calcolo di un numero combinatorio

Successivamente, determineremo passo dopo passo il valore di un numero combinatorio come esempio, così potrai vedere come è fatto:

Calcola il valore del numero combinatorio 5 su 3.

Il coefficiente binomiale di 5 su 3 corrisponde alla seguente espressione:

$\begin{pmatrix}5 \\ 3 \end{pmatrix}$

Pertanto, se applichiamo la formula dei numeri combinatori, per determinarne il valore dobbiamo eseguire le seguenti operazioni:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!(5-3)!}$

O equivalente:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!\cdot 2!}$

Troviamo quindi i fattoriali:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{1\cdot 2 \cdot 3 \cdot 4 \cdot 5}{(1\cdot 2 \cdot 3) \cdot (1\cdot 2)}$

La moltiplicazione 1·2·3 viene ripetuta al numeratore e al denominatore, quindi la frazione può essere semplificata eliminando questo fattore:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{\cancel{1\cdot 2 \cdot 3} \cdot 4 \cdot 5}{(\cancel{1\cdot 2 \cdot 3)} \cdot (1\cdot 2)}$

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{ 4 \cdot 5}{1\cdot 2}$

Adesso calcoliamo i prodotti:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{20}{2}$

Ed infine facciamo la divisione:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \bm{10}$

Proprietà del numero combinatorio

I numeri combinatori, o coefficienti binomiali, possono essere combinati secondo le seguenti proprietà:

Due numeri combinatori complementari sono quelli che hanno lo stesso numeratore n e la somma dei loro ordini è equivalente a detto numeratore. Pertanto, il risultato di due numeri combinatori complementari è identico.

$\begin{pmatrix}n \\ k \end{pmatrix} = \begin{pmatrix}n \\ n-k \end{pmatrix}$

Questa caratteristica dei numeri combinatori è anche chiamata identità di simmetria.

Ad esempio, 6 su 4 dà lo stesso risultato di 6 su 2, perché 6-4=2.

$\begin{pmatrix}6 \\ 4 \end{pmatrix} =\cfrac{6!}{4!(6-4)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(\cancel{1\cdot 2 \cdot 3\cdot 4})\cdot (1\cdot 2)}= \cfrac{30}{2} = \bm{15}$

$\begin{pmatrix}6 \\ 2 \end{pmatrix} =\cfrac{6!}{2!(6-2)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(1\cdot 2)\cdot (\cancel{1\cdot 2 \cdot 3\cdot 4})}= \cfrac{30}{2} = \bm{15}$

La somma di due numeri combinatori con lo stesso numeratore e ordini successivi è uguale a un altro numero combinatorio il cui numeratore è equivalente al numeratore delle addizioni più 1 e il cui ordine corrisponde al valore massimo degli ordini delle addizioni. In altre parole, è sempre soddisfatta la seguente condizione:

$\begin{pmatrix}n\\ k \end{pmatrix} + \begin{pmatrix}n\\ k+1 \end{pmatrix}= \begin{pmatrix}n+1\\ k+1 \end{pmatrix}$

Per esempio:

$\begin{pmatrix}9\\ 2 \end{pmatrix} + \begin{pmatrix}9\\ 3 \end{pmatrix}= \begin{pmatrix}10\\ 3 \end{pmatrix}$

Questa proprietà è conosciuta anche come regola di Pascal.

D’altra parte, questa formula può essere applicata anche al contrario per scomporre un numero combinatorio in due numeri combinatori più semplici:

$\begin{pmatrix}n\\ k \end{pmatrix} = \begin{pmatrix}n-1\\ k-1 \end{pmatrix}+ \begin{pmatrix}n-1\\ k \end{pmatrix}$

Ad esempio, il numero combinatorio 8 su 4 è uguale a 7 su 3 più 7 su 4:

$\begin{pmatrix}8\\ 4 \end{pmatrix} = \begin{pmatrix}7\\ 3 \end{pmatrix}+ \begin{pmatrix}7\\ 4 \end{pmatrix}$

Qualsiasi numero positivo maggiore di 1 è uguale al numero stesso.

$\begin{pmatrix}n\\ 1 \end{pmatrix} =n$

La ragione di questa proprietà è che il fattoriale di un numero è uguale al fattoriale del numero precedente moltiplicato per il numero stesso:

$\begin{pmatrix}n \\ 1 \end{pmatrix} =\cfrac{n!}{1!(n-1)!} = \cfrac{n\cdot (n-1) \cdot (n-2)\cdots 1}{(n-1) \cdot (n-2)\cdots 1}= n$

Esempi di questo tipo di numeri combinatori:

$\begin{pmatrix}12\\ 1 \end{pmatrix} =12 \qquad \begin{pmatrix}5\\ 1 \end{pmatrix} =5 \qquad \begin{pmatrix}9\\ 1 \end{pmatrix} =9$

Qualsiasi numero positivo maggiore di 0 è uguale a uno.

$\begin{pmatrix}n\\ 0 \end{pmatrix} =1$

Infatti, il denominatore della frazione di tale numero combinatorio sarà sempre uguale al numeratore della frazione:

$\begin{pmatrix}n\\ 0 \end{pmatrix} =\cfrac{n!}{0!(n-0)!} =\cfrac{n!}{n!} = 1$

Esempi di numeri combinatori come questo:

$\begin{pmatrix}6\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}2\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}23\\ 0 \end{pmatrix} =1$

Ogni numero su se stesso è uguale a 1.

$\begin{pmatrix}n\\ n \end{pmatrix} =1$

Ecco la demo:

$\begin{pmatrix}n\\ n \end{pmatrix} =\cfrac{n!}{n!(n-n)!} =\cfrac{n!}{n!\cdot 0!}= \cfrac{n!}{n!} = 1$

Esempi di numeri combinatori come questo:

$\begin{pmatrix}5\\ 5 \end{pmatrix} =1 \qquad \begin{pmatrix}37\\ 37 \end{pmatrix} =1 \qquad \begin{pmatrix}14\\ 14 \end{pmatrix} =1$

Come calcolare un numero combinatorio con la calcolatrice

Finora abbiamo visto come trovare un numero combinatorio di numeri più o meno semplici, ma quando dobbiamo operare con quantità molto grandi è meglio utilizzare la calcolatrice per determinare il numero combinatorio. Vedremo ora come inserire un numero combinatorio nella calcolatrice.

Quindi, la chiave utilizzata per calcolare un numero combinatorio con la calcolatrice è la chiave nCr . E per determinare il valore del numero combinatorio, devi prima inserire il numeratore del numero combinatorio, poi premere il tasto nCr, quindi inserire l’ordine del numero combinatorio e infine premere il tasto uguale.

$\begin{pmatrix}n\\ k \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} n \rightarrow \boxed{nCr} \rightarrow k \rightarrow \boxed{=}$

Sulle calcolatrici scientifiche CASIO, il tasto nCr solitamente ha un proprio pulsante o si trova sopra il pulsante di divisione, a seconda del modello.

Ad esempio, se vogliamo sapere qual è il numero combinatorio 10 su 6, dobbiamo eseguire la seguente sequenza:

$\begin{pmatrix}10\\ 6 \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} 10 \rightarrow \boxed{nCr} \rightarrow 6 \rightarrow \boxed{=} \rightarrow 210$

Applicazioni del numero combinatorio

Se sei arrivato fin qui, probabilmente sai già come risolvere qualsiasi numero combinatorio, perfetto. Ma… a cosa serve il numero combinatorio? Bene, allora vedremo tutti i vantaggi che questo tipo di operazione molto particolare presenta.

Combinatoria

Come abbiamo visto in cima alla pagina, il risultato di un numero combinatorio

$\begin{pmatrix}n\\ k \end{pmatrix}$

rappresenta il numero di possibili gruppi di

$k$

elementi che possono essere formati da un insieme di un totale di

$n$

elementi.

Pertanto, alcuni problemi combinatori possono essere risolti utilizzando numeri combinatori (o coefficienti binomiali). Vediamo come farlo utilizzando un esempio:

In una classe di 30 studenti, vogliamo scegliere un gruppo di 4 studenti per svolgere determinati compiti. Qual è il numero totale di gruppi diversi che possono essere formati?

In questo caso l’ordine degli studenti non ha importanza, lo stesso studente non si ripete due volte all’interno del gruppo e non tutti gli studenti entrano nel gruppo. Pertanto, la formula del numero combinatorio può essere utilizzata per determinare in quanti modi può essere formato il gruppo.

Per fare questo devi calcolare il numero combinatorio avendo come numeratore il numero totale degli studenti e come ordine il numero degli studenti che formeranno il gruppo:

$\begin{pmatrix}30 \\ 4 \end{pmatrix} =\cfrac{30!}{4!(30-4)!} =\cfrac{30\cdot 29 \cdot 28 \cdot 27 \cdot \cancel{26!}}{4\cdot 3 \cdot 2 \cdot 1 \cdot \cancel{26!}} = \cfrac{657720}{24}=\bm{27405}$

Il numero totale di combinazioni possibili è quindi di 27.405 gruppi.

Il binomio di Newton

Un’altra applicazione dei numeri combinatori è il binomio di Newton. Il binomio di Newton è un polinomio composto da due termini elevati insieme a numero intero, vale a dire che il binomio di Newton è quel polinomio che risponde alla seguente espressione algebrica:

$(a+b)^n$

Ovviamente, se il binomio è quadrato, significa che si tratta di un’identità notevole e, quindi, può essere facilmente calcolata con la formula corrispondente. Quando invece il binomio viene elevato a numeri grandi, il calcolo diventa piuttosto difficile. Ebbene, il teorema binomiale di Newton dice che questi tipi di polinomi possono essere calcolati molto facilmente da numeri combinatori.

Clicca il seguente link e scopri cos’è la formula binomiale di Newton e come viene calcolata. Inoltre, potrai vedere esempi ed esercitarti con esercizi risolti passo dopo passo. E infine scoprirai la curiosa storia di questo teorema.

Triangolo di Tartaglia (o di Pascal).

Come hai visto in questo articolo, calcolare manualmente il coefficiente binomiale di grandi numeri può essere laborioso e complicato.

D’altra parte, con il triangolo di Tartaglia, detto anche triangolo di Pascal, tutti i numeri combinatori possono essere facilmente determinati utilizzando una regola mnemonica. Questo è logicamente molto utile poiché fa risparmiare molto tempo durante i calcoli.

Per scoprire esattamente come farlo, vedere la spiegazione del triangolo di Tartaglia . In questa pagina collegata scoprirai cos’è questo misterioso triangolo, a cosa serve (ha applicazioni sorprendenti) 😮 e qual è la sua origine (era usato già più di 1000 anni fa).

Esercizi sui numeri combinatori risolti

Affinché tu possa esercitarti e comprendere appieno i concetti spiegati, ti lasciamo diversi esercizi risolti passo dopo passo sui numeri combinatori.

Esercizio 1

Trova il numero combinatorio 9 per 5 (senza usare la calcolatrice).

Vedi la soluzione

Per trovare il valore del numero combinatorio 9 su 5 applichiamo semplicemente la formula fattoriale:

$\begin{pmatrix}9 \\ 5 \end{pmatrix} =\cfrac{9!}{5!(9-5)!} = \cfrac{9\cdot 8 \cdot 7\cdot 6\cdot \cancel{5!}}{\cancel{5!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{3024}{24} = \bm{126}$

Esercizio 2

Qual è il risultato della seguente somma di due numeri combinatori? (senza calcolatrice)

$\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}$

Vedi la soluzione

Dalle proprietà dei numeri combinatori segue che la somma del problema è uguale al seguente numero combinatorio:

$\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}=\begin{pmatrix}11\\ 7 \end{pmatrix}$

Pertanto è sufficiente calcolare il numero combinatorio 11 su 7:

$\begin{pmatrix}11 \\ 7 \end{pmatrix} =\cfrac{11!}{7!(11-7)!} = \cfrac{11\cdot 10 \cdot 9\cdot 8 \cdot \cancel{7!}}{\cancel{7!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{7920}{24} = \bm{330}$

Esercizio 3

Determina se i seguenti numeri combinatori sono uguali:

$\begin{pmatrix}6\\ 0 \end{pmatrix} \qquad \begin{pmatrix}6\\ 1 \end{pmatrix}\qquad \begin{pmatrix}6\\ 6 \end{pmatrix}$

Vedi la soluzione

Per trovare il risultato dei tre numeri combinatori non è necessario usare la calcolatrice, ma si possono trovare facilmente grazie alle proprietà dei numeri combinatori.

Innanzitutto, un numero combinatorio di qualsiasi numero maggiore di 0 dà 1. Pertanto:

$\begin{pmatrix}6\\ 0 \end{pmatrix} =1$

D’altra parte qualsiasi numero maggiore di uno è uguale al numero stesso. Ancora:

$\begin{pmatrix}6\\ 1 \end{pmatrix} =6$

E infine, qualsiasi numero combinatorio formato dallo stesso numero ripetuto due volte equivale a 1. Quindi:

$\begin{pmatrix}6\\ 6 \end{pmatrix} =1$

In conclusione, il primo e il terzo numero combinatorio nel problema sono uguali, tuttavia sono diversi dal numero combinatorio medio.

$\begin{pmatrix}6\\ 0 \end{pmatrix}= \begin{pmatrix}6\\ 6 \end{pmatrix}\neq \begin{pmatrix}6\\ 1 \end{pmatrix}$

Numero combinatorio (o coefficiente binomiale)

Cos’è un numero combinatorio?

Formula dei numeri combinatori

Esempio di calcolo di un numero combinatorio

Proprietà del numero combinatorio

Come calcolare un numero combinatorio con la calcolatrice

Applicazioni del numero combinatorio

Combinatoria

Il binomio di Newton

Triangolo di Tartaglia (o di Pascal).

Esercizi sui numeri combinatori risolti

Esercizio 1

Esercizio 2

Esercizio 3

Lascia un commento Annulla risposta