Questa pagina spiega cos’è il prodotto vettoriale di due vettori e come viene calcolato. Vedrai anche come trovare la direzione e l’orientamento del prodotto incrociato utilizzando la regola della mano destra (o del cavatappi). E in più troverai gli utilizzi di questo tipo di operazioni, oltre ad esempi, esercizi e problemi risolti passo dopo passo.
Qual è il prodotto vettoriale di due vettori?
In matematica, il prodotto incrociato è un’operazione tra due vettori nello spazio tridimensionale (in R3). Il risultato di questa operazione vettoriale è un vettore con direzione perpendicolare ai due vettori moltiplicati e con modulo pari al prodotto dei moduli dei vettori moltiplicatori per il seno dell’angolo che formano. In altre parole, la sua formula è:
![]()
Come vedi nella formula precedente, il prodotto incrociato è indicato
![]()
, motivo per cui è anche chiamato prodotto incrociato. A volte viene anche chiamato prodotto vettoriale di Gibbs, poiché lo ha inventato.
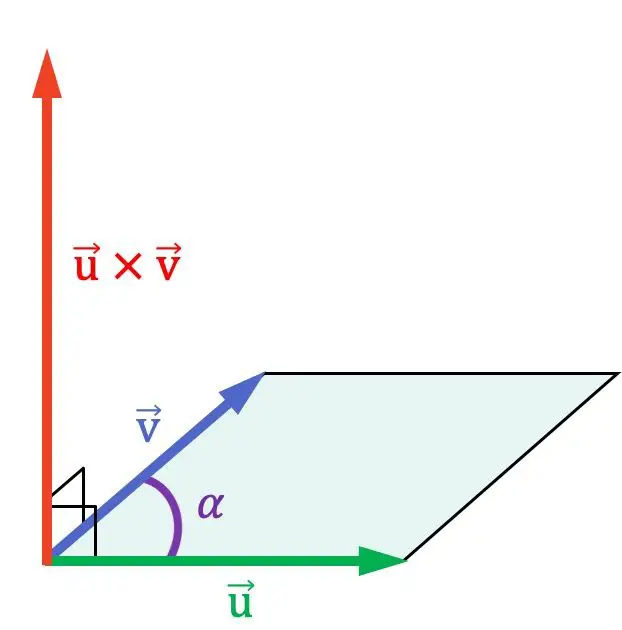
Come puoi vedere nella rappresentazione grafica precedente, il prodotto vettoriale è perpendicolare ai due vettori che si moltiplicano e, quindi, è normale al piano che li contiene.
Formula per calcolare il prodotto vettoriale di due vettori
Se conosciamo le coordinate cartesiane dei vettori, il modo più semplice per calcolare il loro prodotto incrociato è risolvere un determinante 3×3. Guarda come è fatto:
Consideriamo due vettori qualsiasi:
![]()
Il suo prodotto vettoriale è:
![Rendered by QuickLaTeX.com \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-56551111a4f5a18a4609772ebaeaf919_l3.png)
Dove i vettori
![]()
Questi sono i versori rispettivamente nelle direzioni degli assi X, Y e Z.
Vediamo un esempio di come calcolare il prodotto vettoriale tra due vettori:
![]()
Per determinare il prodotto vettoriale tra i vettori, dobbiamo creare il seguente determinante di ordine 3:
![Rendered by QuickLaTeX.com \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-abc77b698bf6f4fddec1ab2dcc8b07f0_l3.png)
In questo caso, risolveremo il determinante mediante adiuvanti o cofattori (si potrebbe utilizzare anche la regola di Sarrus):
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix} & = \vv{i}\begin{vmatrix} 1 & 0 \\[1.1ex] 1&-1 \end{vmatrix} -\vv{j}\begin{vmatrix} 3& 0 \\[1.1ex] 2 &-1 \end{vmatrix}+\vv{z}\begin{vmatrix}3& 1 \\[1.1ex] 2 &1 \end{vmatrix} \\[2ex] & = -\vv{i}+3\vv{j}+\vv{z}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eeeac04b3f0edd64e5413629051551fd_l3.png)
Il risultato del prodotto vettoriale dei due vettori è quindi:
![]()
Determina la direzione e la direzione del prodotto vettoriale
A volte non è necessario conoscere le componenti del vettore risultante dal prodotto vettoriale, ma è sufficiente trovare il suo modulo, la sua direzione e il suo verso. Ciò accade spesso in fisica, soprattutto nel calcolo delle forze.
Esistono quindi diverse regole per trovare la direzione e la direzione del prodotto vettoriale, le più conosciute sono la regola della mano destra , con tre dita o con tutta la mano, e la regola del cavatappi (o della vite) . Puoi usarne una qualsiasi, quindi non è necessario conoscerle tutte, ti spiegheremo comunque le tre regole in modo che tu possa attenerti a quella che ti piace di più. 😉
Regola della mano destra (3 dita)
La versione a 3 dita della regola o legge della mano destra prevede l’esecuzione dei seguenti passaggi:
- Posiziona l’indice della mano destra verso il primo vettore del prodotto incrociato

- Posiziona il dito medio (o il dito medio) della mano destra verso il secondo vettore del prodotto incrociato

- La posizione del pollice risultante indica la direzione e la direzione del prodotto incrociato

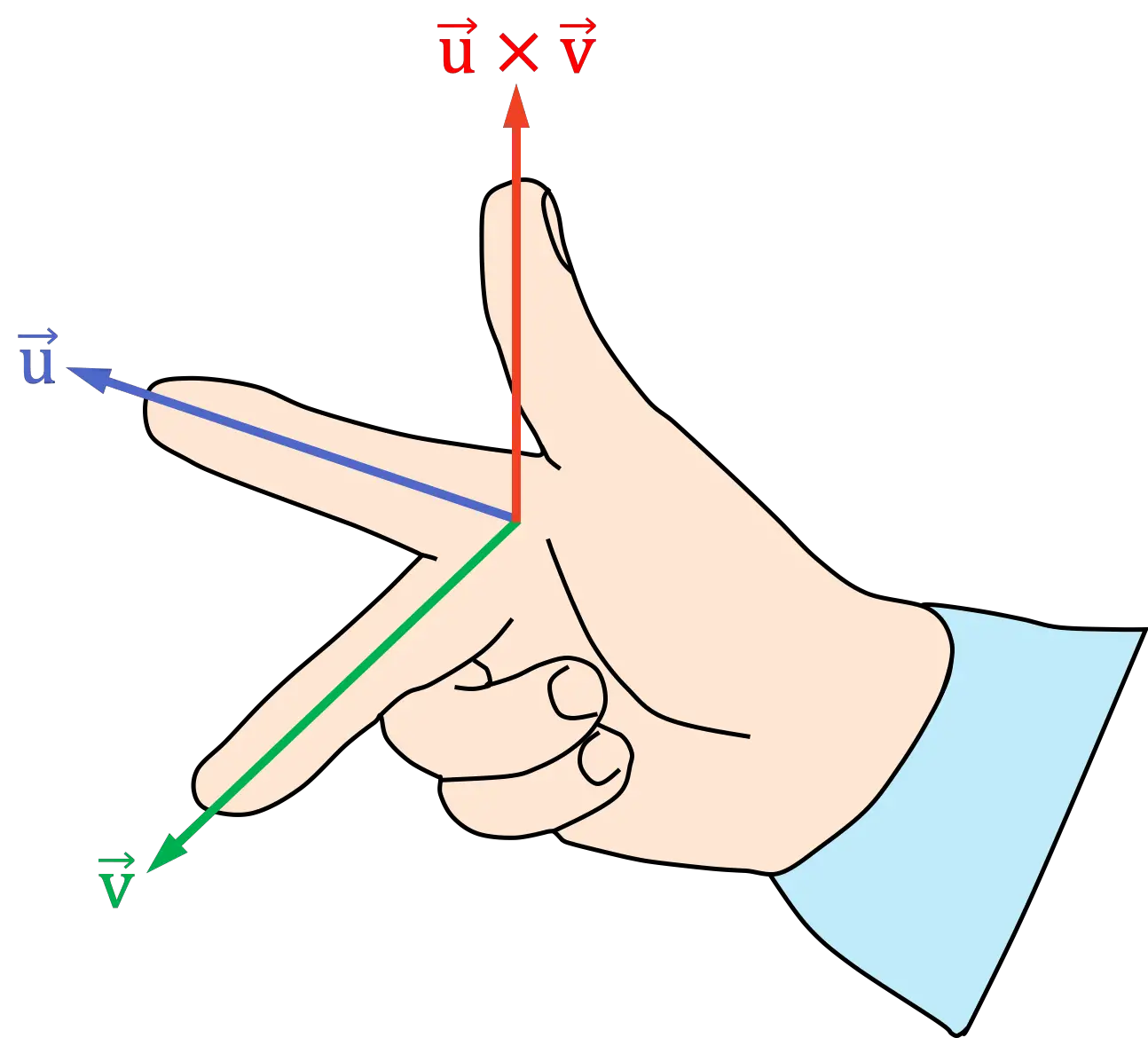
Regola della mano destra (palmo della mano)
La versione palmare della regola o legge della mano destra è molto simile alla regola precedente. Per applicarlo è necessario seguire i seguenti passaggi:
- Metti la mano destra che punta con le dita nella stessa direzione del primo vettore del prodotto incrociato

- Chiudi la mano destra spostando le dita verso il secondo vettore del prodotto incrociato

Devi chiudere la mano sul lato in cui l’angolo (o la distanza) tra i vettori è più piccolo.
- La posizione risultante del pollice determina la direzione del prodotto incrociato

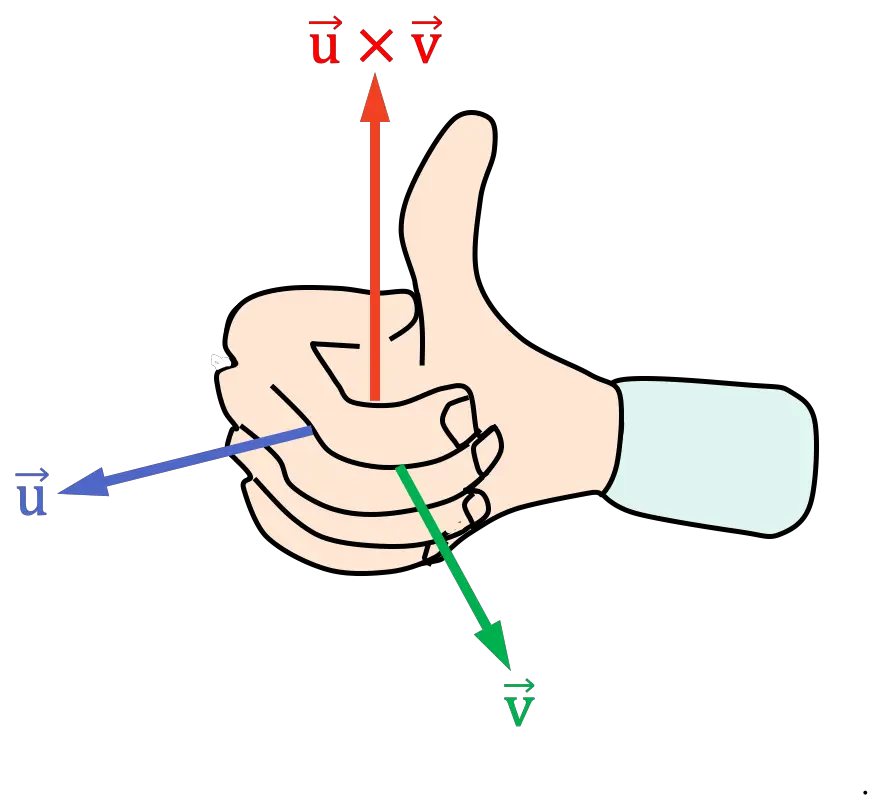
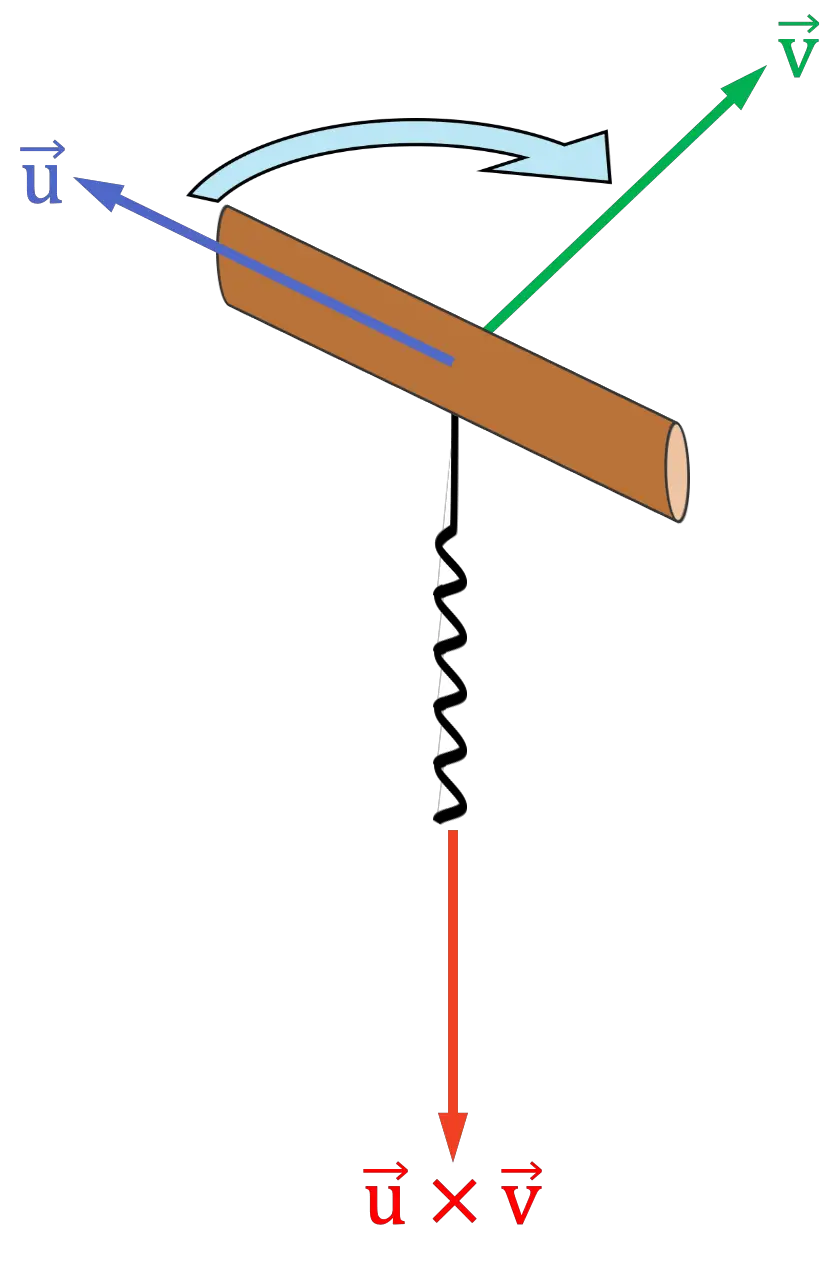
regola del cavatappi
La regola del cavatappi o della vite è simile alla regola della mano destra che utilizza l’intero palmo della mano. La procedura è la seguente:
- Usando la tua immaginazione, posiziona un cavatappi (o una vite) con la maniglia rivolta nella stessa direzione del primo vettore del prodotto incrociato.

- Quindi ruotare il cavatappi verso il secondo vettore del prodotto incrociato
come se lo mettessi in un tappo di sughero. È necessario girare il cavatappi sul lato in cui la distanza tra i vettori è più breve.
- La direzione in cui punta la spirale del cavatappi sarà la direzione e la direzione del prodotto vettoriale

Proprietà del prodotto vettoriale di due vettori
Il prodotto vettoriale di due vettori ha le seguenti caratteristiche:
- Proprietà anticommutativa: l’ordine dei vettori coinvolti nel prodotto vettoriale non è indifferente, perché il segno varia in base ad esso.
![]()
- Proprietà distributiva relativa all’addizione e alla sottrazione di vettori:
![]()
![]()
- Proprietà omogenea : moltiplicare un vettore del prodotto vettoriale per uno scalare (un numero reale) equivale a moltiplicare il risultato del prodotto vettoriale per detto scalare.
![]()
- Il vettore risultante dal prodotto vettoriale è perpendicolare ai due vettori coinvolti nell’operazione.
![Rendered by QuickLaTeX.com \begin{array}{c} \vv{\text{u}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \\[2ex] \vv{\text{v}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6a96345e09a0fdb952557c9138c72ac4_l3.png)
- Inoltre, se i due vettori sono ortogonali, sono soddisfatte le seguenti equazioni:
![Rendered by QuickLaTeX.com \vv{\text{u}} \perp \vv{\text{v}} \ \longrightarrow \ \begin{cases} \vv{\text{u}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \\[2ex] \vv{\text{v}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d49d463798c6381c9a8c065417ee3dbf_l3.png)
- Il prodotto vettoriale di due vettori paralleli è uguale al vettore zero (o zero).
![]()
- Se non conosciamo l’angolo formato da due vettori, il modulo del loro prodotto vettoriale può essere calcolato anche utilizzando la seguente espressione:
![]()
Calcola l’area di un parallelogramma o di un triangolo utilizzando il prodotto vettoriale
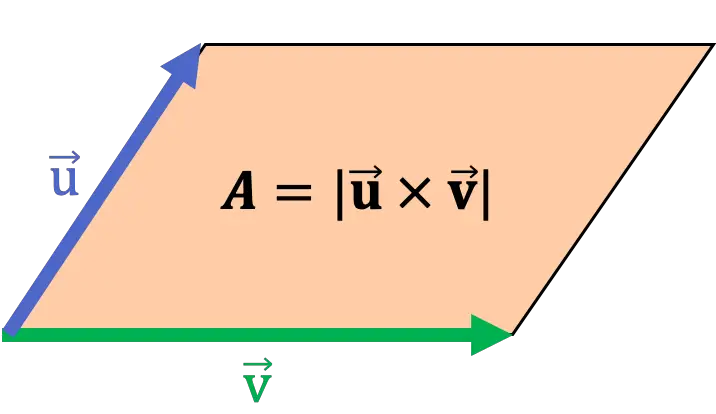
Geometricamente, il modulo del prodotto vettoriale di due vettori coincide con l’area del parallelogramma che ha come lati questi due vettori. Pertanto, il prodotto incrociato può essere utilizzato per calcolare l’area di un parallelogramma.
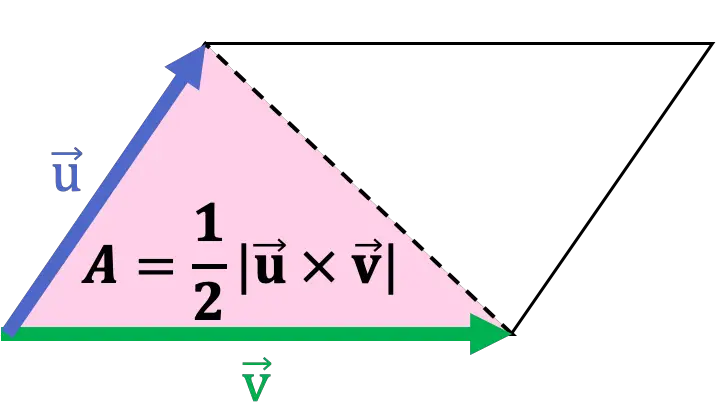
Inoltre, la diagonale di un parallelogramma lo divide in due triangoli o, in altre parole, un triangolo è la metà di un parallelogramma. Pertanto, l’ area di un triangolo è la metà del modulo del prodotto incrociato prendendo due dei suoi lati come vettori.
Ricordiamo che il modulo di un vettore in uno spazio tridimensionale è la radice della somma dei quadrati delle sue coordinate:
![]()
Queste sono due delle applicazioni del prodotto vettoriale di due vettori nel campo della matematica. Tuttavia ha anche altri usi, ad esempio in fisica viene utilizzato per calcolare il campo magnetico.
Esercizi risolti sui prodotti vettoriali di vettori
Esercizio 1
Calcolare il prodotto vettoriale tra i seguenti due vettori:
![]()
Per determinare il prodotto vettoriale tra i vettori, dobbiamo risolvere il seguente determinante di dimensione 3×3:
![Rendered by QuickLaTeX.com \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-44db63ee02936f6e5f21891c3e412fb6_l3.png)
In questo caso risolveremo il determinante mediante adiuvanti o cofattori (ma si potrebbe usare anche la regola di Sarrus):
![Rendered by QuickLaTeX.com \begin{aligned}\begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1\end{vmatrix} & = \vv{i}\begin{vmatrix} 4 & 2 \\[1.1ex]-2&1\end{vmatrix} -\vv{j}\begin{vmatrix} -1& 2 \\[1.1ex] 0 &1\end{vmatrix}+\vv{z}\begin{vmatrix}-1& 4 \\[1.1ex] 0 &-2\end{vmatrix} \\[2ex] & = 8\vv{i}+\vv{j}+2\vv{z}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fe298c37814c92498e4fd8ade0620951_l3.png)
Il risultato del prodotto vettoriale dei due vettori è quindi:
![]()
Esercizio 2
Trova il prodotto vettoriale tra i seguenti due vettori:
![]()
Per trovare il prodotto vettoriale tra i due vettori, dobbiamo risolvere il seguente determinante 3×3:
![Rendered by QuickLaTeX.com \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6a23d8e45f9065f70c576e6b8db02465_l3.png)
In questo caso, risolveremo il determinante mediante aggiunti o cofattori (sebbene la regola di Sarrus possa essere utilizzata in modo intercambiabile):
![Rendered by QuickLaTeX.com \begin{aligned} \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3\end{vmatrix} & = \vv{i}\begin{vmatrix} -2 & 4 \\[1.1ex] 5&-3\end{vmatrix} -\vv{j}\begin{vmatrix} 3& 4 \\[1.1ex] 1&-3\end{vmatrix}+\vv{z}\begin{vmatrix}3& -2 \\[1.1ex] 1 &5\end{vmatrix} \\[2ex] & = -14\vv{i}+13\vv{j}+17\vv{z}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-02ffb40666893faa7677234065f3f85f_l3.png)
Il risultato del prodotto vettoriale tra i due vettori è quindi:
![]()
Esercizio 3
Conoscendo i moduli di due vettori e l’angolo che formano:
![]()
Determinare l’entità del prodotto vettoriale dei due vettori.
Possiamo facilmente calcolare il modulo del prodotto vettoriale tra i due vettori applicando la formula:
![Rendered by QuickLaTeX.com \begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 5 \cdot 6 \cdot \text{sen}(30º) \\[2ex] &= 30 \cdot 0,5 \\[2ex] &= \bm{15} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-06dcff41e0dcf31152f0047507056f24_l3.png)
Esercizio 4
Dai seguenti vettori contenuti nel piano dello schermo:
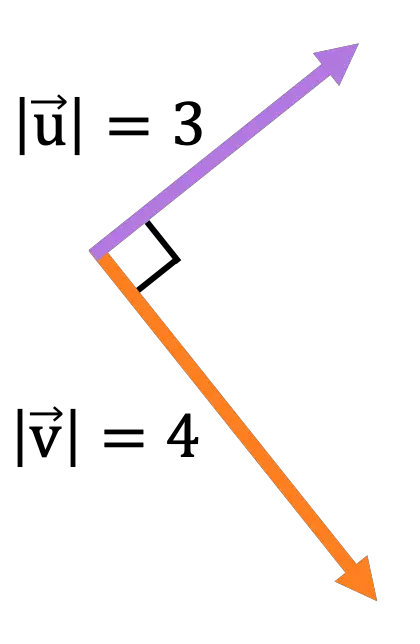
Calcolare la grandezza, la direzione e il senso del vettore risultante dalla seguente operazione vettoriale:
![]()
I due vettori sono perpendicolari, quindi la norma del prodotto vettoriale sarà:
![Rendered by QuickLaTeX.com \begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 3 \cdot 4 \cdot \text{sen}(90º) \\[2ex] &= 12 \cdot 1 \\[2ex] &= \bm{12} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d8f675fe7eb44c050c508c4771c0a439_l3.png)
Invece il vettore risultante dal prodotto vettoriale è perpendicolare ai due vettori che partecipano all’operazione, la sua direzione sarà quindi perpendicolare allo schermo.
Ed infine, utilizzando la regola della linea retta (o del cavatappi), possiamo dedurre che la direzione del vettore risultante sarà verso l’interno dello schermo.
Esercizio 5
Calcola l’area del parallelogramma che ha come lati i seguenti vettori:
![]()
L’area di un parallelogramma coincide con il modulo del prodotto vettoriale dei vettori che lo compongono. Calcoliamo quindi il prodotto vettoriale dei vettori:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& 3 & -2 \\[1.1ex] 5 &0&-1\end{vmatrix} & = \vv{i}\begin{vmatrix} 3 & -2 \\[1.1ex] 0&-1\end{vmatrix} -\vv{j}\begin{vmatrix} 2& -2 \\[1.1ex] 5 &-1\end{vmatrix}+\vv{z}\begin{vmatrix}2& 3 \\[1.1ex] 5 &0\end{vmatrix} \\[2ex] & = -3\vv{i}-8\vv{j}-15\vv{z}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e7c1825be82d94c4eae49c73f509858_l3.png)
E poi il tuo modulo:
![]()
Esercizio 6
Trova l’area del triangolo i cui vertici sono i seguenti punti:
![]()
Innanzitutto dobbiamo calcolare i vettori che formano i lati del triangolo:
![]()
![]()
L’area di un triangolo è la metà del valore del prodotto vettoriale dei vettori che lo compongono. Calcoliamo quindi il prodotto vettoriale dei vettori:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& -1 & 3 \\[1.1ex] -5 &2&0\end{vmatrix} & = \vv{i}\begin{vmatrix} -1 & 3 \\[1.1ex] 2&0\end{vmatrix} -\vv{j}\begin{vmatrix} 2& 3 \\[1.1ex] -5 &0\end{vmatrix}+\vv{z}\begin{vmatrix}2& -1 \\[1.1ex] -5 &2\end{vmatrix} \\[2ex] & = -6\vv{i}-15\vv{j}-\vv{z}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-42a0ae5858bcb681ee92ec1ed67424c7_l3.png)
Dopo il modulo:
![]()
E infine, l’area del triangolo sarà la metà del modulo:
![]()