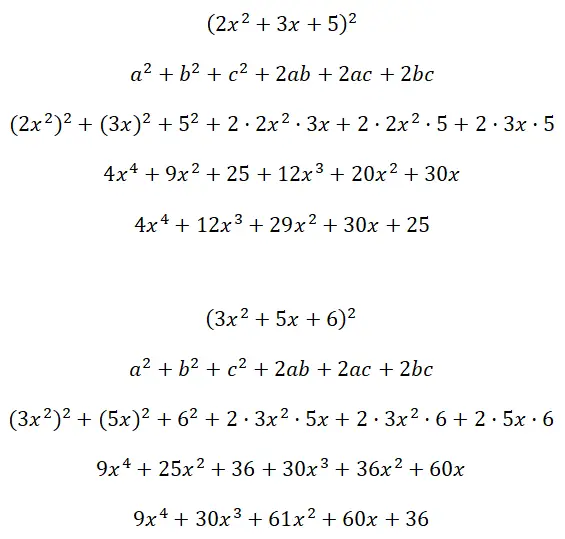Quali sono i prodotti straordinari o le identità straordinarie?
Le identità notevoli , chiamate anche prodotti notevoli o uguaglianze notevoli , sono risorse matematiche che consentono di risolvere più rapidamente prodotti e quozienti di polinomi . Come indica la parola identità, si tratta di uguaglianze che ci permettono di calcolare queste operazioni senza doverle risolvere. Poiché sappiamo che questa espressione segue regole fisse (che vengono sempre rispettate) e, quindi, possiamo ottenere il risultato senza doverlo verificare.
Quando utilizzare un’identità notevole?
Queste identità vengono utilizzate principalmente nel campo dell’algebra e la loro funzione principale è quella di velocizzare la soluzione di un determinato polinomio, senza dover risolvere l’intera operazione stessa. Da lì otteniamo le formule di prodotti degni di nota, che commenteremo nel corso dell’articolo. E infine, possiamo applicare le formule a quadrati completi, scomporre polinomi o qualsiasi altro tipo di calcolo.
Come risolvere passo dopo passo un prodotto straordinario?
Per risolvere le identità notevoli è necessario seguire una procedura molto semplice, ma anche molto sensata:
- Identificare il tipo di identità notevole: il primo passo è identificare il tipo di operazione: un prodotto notevole o un quoziente notevole. Dovresti anche chiarire quale tipo di formula dovrai applicare, anche se lo capirai più avanti, una volta che avremo spiegato i diversi tipi di identità notevoli.
- Applica la formula: una volta che sai quale formula devi applicare, è il momento di fare i calcoli. A seconda del tipo di identità, dovrai risolvere operazioni più o meno complesse e, nella stragrande maggioranza dei casi, questi calcoli saranno costituiti da termini che contengono almeno un’incognita.
- Semplifica l’espressione: infine, quando ottieni il risultato, devi semplificarlo. In questo passaggio, devi raggruppare termini simili e ordinarli per formare un polinomio risultante ben strutturato. Va notato che questo passaggio è importante quanto gli altri, perché altrimenti l’esercizio rimane incompleto.
Formule di identità notevoli o principali prodotti notevoli
Di seguito troverete tutte le formule corrispondenti alle identità notevoli. Oltre alla spiegazione teorica di ogni caso, sono presenti anche alcuni notevoli esempi di prodotti risolti, attraverso i quali comprenderete meglio tutti i concetti. Vale la pena ricordare che in questa prima sezione troverai solo le identità più importanti . Ma, leggendo questo articolo, imparerai come sviluppare prodotti degni di nota più complessi, come quelli composti da trinomi.
quadrato di una somma
Il primo caso riguarda il quadrato della somma , che è un’espressione polinomiale molto comune nel mondo dell’algebra. Questo si può trovare scritto come: (a + b) 2 , che equivale a: (a + b) · (a + b). Pertanto sappiamo che può essere risolto utilizzando la moltiplicazione polinomiale. Ma, grazie alle identità notevoli, possiamo risparmiare tempo utilizzando la seguente formula: (a + b) 2 = a 2 + 2ab + b 2 . Successivamente vi mostriamo la dimostrazione della formula che abbiamo appena visto, in questo modo potrete capire da dove viene e come si utilizza:
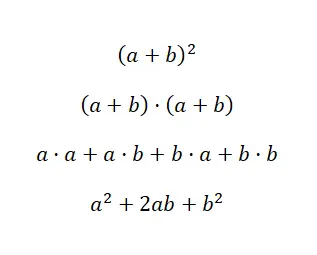
Come possiamo vedere, abbiamo effettuato la verifica utilizzando la moltiplicazione dei polinomi che abbiamo commentato in precedenza. E possiamo dire con assoluta certezza che se conosci a memoria la formula risultante, eseguendo una semplice sostituzione di valori , puoi ottenere il risultato più velocemente. Quindi è un concetto matematico molto utile. Ora che sai come funziona il quadrato di una somma, ti mostriamo un esempio concreto:
Esempio del quadrato di una somma
Calcolare l’identità notevole (2x + 4) 2 :
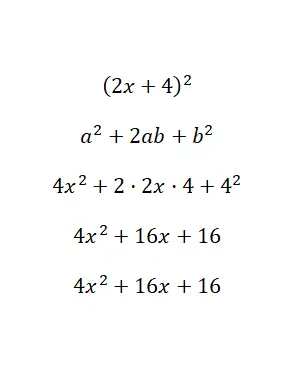
In pratica abbiamo associato i valori del binomio alle lettere della formula e abbiamo risolto: a = 2x e b = 4. Infine, dopo aver risolto tutti i calcoli, otteniamo il polinomio 4x 2 + 16x + 16, che è equivalente all’originale . In questo esempio abbiamo ottenuto un polinomio espanso (in forma standard) da un polinomio ridotto.
quadrato di una sottrazione
Un’altra espressione molto comune è il quadrato della sottrazione , che è molto simile al quadrato dell’addizione, cambia solo di un segno. Allora la struttura del binomio è equivalente a: (a – b) 2 , e se la spieghiamo otteniamo: (a – b) · (a – b). Come nel caso precedente, questo può essere calcolato da una moltiplicazione di polinomi, sebbene abbia anche una formula che facilita la soluzione: a 2 – 2ab +b 2 . Di seguito potete trovare la prova empirica di ciò:
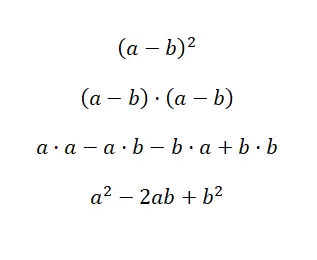
Per semplificare la risoluzione del quadrato di una differenza, possiamo usare la stessa formula che abbiamo usato per la somma di un quadrato, ma con il primo segno negativo . Questa modifica minima permette di adattare l’espressione ai binomi composti da un termine positivo e da un termine negativo, utile per le sottrazioni. Ora ti mostreremo un esempio risolto:
Esempio del quadrato di una sottrazione
Calcolare l’identità notevole (x – 3) 2 :
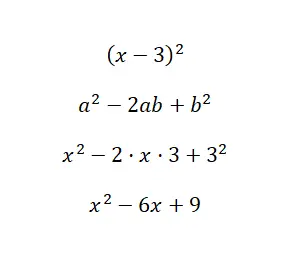
Come puoi vedere nella soluzione di esempio, abbiamo sostituito i valori del nostro binomio nella formula, a = x e b = 3. Pertanto, utilizzando la formula che abbiamo spiegato prima, dobbiamo solo fare la sostituzione e alcune operazioni molto basilari calcoli. Questo ci permette di vedere con quanta facilità si può calcolare il quadrato di una differenza con questa espressione.
Differenza di quadrati o somma per differenza
Il terzo caso di prodotti notevoli è detto differenza dei quadrati , questa è formata dal prodotto di un binomio positivo e di un binomio negativo. Un’espressione di questo stile ha la seguente struttura: (a + b) · (a – b), quindi espandendo questo prodotto otteniamo la formula che facilita il calcolo: a 2 – b 2 . Come puoi vedere si tratta di una formula molto semplice, anche se per comprenderla appieno è necessario svolgere tutti i calcoli:
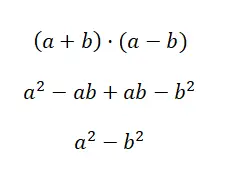
Esempio di somma per differenza
Calcolare l’identità notevole (x + 1) · (x – 4):
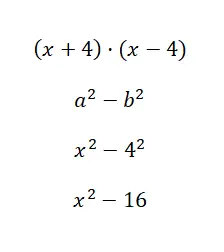
In questa occasione il calcolo numerico è molto semplice, infatti bisognava risolvere solo una potenza. Anche se è vero che questa formula è applicabile solo quando i binomi hanno lo stesso termine principale e lo stesso termine indipendente, ma con segno cambiato. Quindi questa identità è importante, ma non è quella che utilizzerai di più.
Prodotto di due binomi con un termine comune
In questo quarto caso ci troviamo di fronte ad una situazione molto simile alla precedente, anche se con una leggera modifica nella struttura. Osserva la differenza che ti mostriamo: (x + a) · (x + b) e (a + b) · (a – b). Nel caso in cui ancora non lo vedi molto chiaramente, considera il seguente esempio: (x + 4) · (x + 5) e (x + 4) · (x – 4). Nel primo caso (il prodotto di due binomi di termini comuni ) esiste un solo termine condiviso, mentre nel secondo caso (la somma per differenza) i due termini sono comuni, ma il termine indipendente ha il segno invertito. Detto questo vediamo con quale formula possiamo agire:
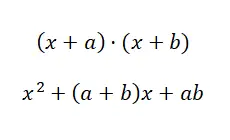
Esempio del prodotto di due binomi con un termine comune
Risolvere per il prodotto notevole (x + 2) · (x + 3):
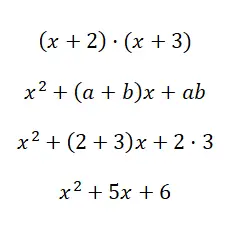
Utilizzando la formula x 2 + (a + b)x + ab possiamo calcolare il polinomio di secondo grado risultante dalla moltiplicazione dei due binomi. Speriamo che attraverso questo esempio tu abbia capito la differenza tra gli ultimi due casi che abbiamo spiegato, perché a volte può essere difficile distinguerli.
quadrato di un trinomio
Quando proviamo a calcolare il quadrato di un trinomio, abbiamo anche un prodotto straordinario che ci semplifica la vita. Questa espressione si rappresenta così: (a + b + c) 2 e il prodotto equivalente è: a 2 + b 2 + c 2 + 2ab + 2ac + 2bc. È bene notare che questo vale nel caso di un trinomio positivo, ma se uno dei coefficienti è negativo è sufficiente scrivere nella formula il valore negativo. Di seguito è riportata la dimostrazione della formula:
Esempio del quadrato di un trinomio
Calcolare l’identità notevole (2x + 1 + x 2 ) 2 :
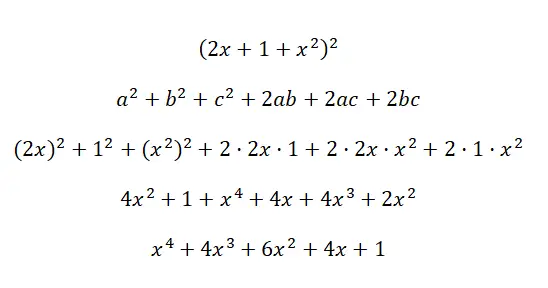
Formule dall’identità notevole o prodotti al cubo notevoli
Ora che abbiamo spiegato le principali identità notevoli, esamineremo le loro derivate , iniziando dai binomi al cubo. Per calcolare i prodotti notevoli di questo stile dovremo ricorrere a formule un po’ più complesse, ma che seguono una struttura simile a quelle di cui abbiamo già parlato.
binomio al cubo
Il cubo di un binomio si scrive: (a + b) 3 e (a – b) 3 , questa espressione equivale alla seguente formula: (a 3 + 3a 2 b + 3ab 2 + b 3 ), e (a 3 – 3a 2 b + 3ab 2 – b 3 ). Questi due casi si chiamano cubo di somma e cubo di sottrazione, perché sono binomi al cubo. Di seguito troverete una dimostrazione molto dettagliata di ciascun caso:
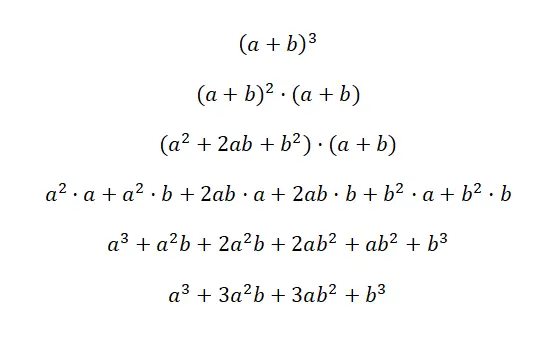
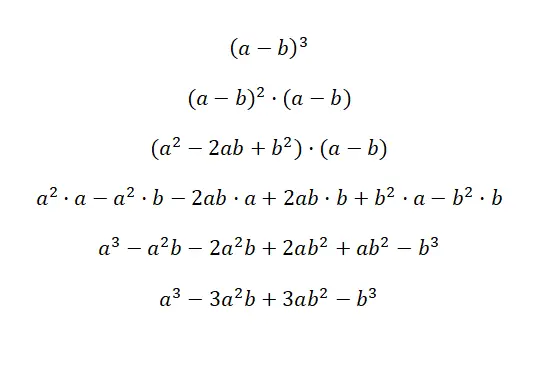
La chiave per comprendere questa prima dimostrazione è capire che (a + b) 3 equivale a: (a + b) 2 · (a + b). In questo modo utilizziamo la formula del quadrato di una somma , che abbiamo spiegato in precedenza, per moltiplicare l’altro fattore. Allora semplifichiamo semplicemente l’espressione, e otteniamo la corrispondente identità notevole: a 3 + 3a 2 b + 3ab 2 + b 3 . Nel caso del secondo esempio avviene la stessa cosa, ma con cambio di segno.
Esempio di cubo binomiale
Risolvi l’identità notevole (x + 3) 3 :
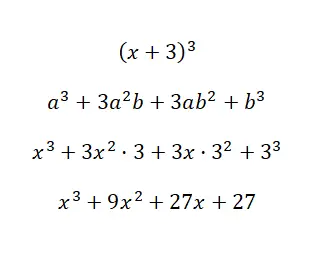
Utilizzando la formula di cui abbiamo appena parlato, possiamo calcolare il polinomio, tenendo conto che: a = xyb = 3. Come potete vedere, la procedura è molto semplice e non presenta molte complicazioni nel calcolo, è perché abbiamo la formula . Altrimenti, dover fare così tante moltiplicazioni sarebbe piuttosto noioso.
Somma di cubi e differenza di cubi
Abbiamo anche quest’altro caso, che può essere facilmente confuso con il precedente. Sebbene i due casi siano scritti diversamente, non sono equivalenti. L’espressione equivalente alla somma o differenza dei cubi è: a 3 + b 3 , mentre nel caso precedente si parlava di: (a + b) 3 . Come puoi vedere, c’è un’innegabile somiglianza nella struttura dell’espressione, ma in realtà, quando si tratta di sviluppare il calcolo, si tratta di due casi completamente diversi:
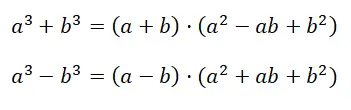
Nella dimostrazione della formula otteniamo la fattorizzazione del primo polinomio , precisamente passiamo dal binomio iniziale al prodotto di un binomio per un trinomio. Sembra che il risultato ottenuto (a + b) · (a 2 – ab + b 2 ), non semplifichi affatto il calcolo, ma in realtà fattorizzando il polinomio otteniamo un’espressione molto semplice da comprendere.
Esempio di somma di cubi
Calcola il prodotto notevole x 3 + 27:
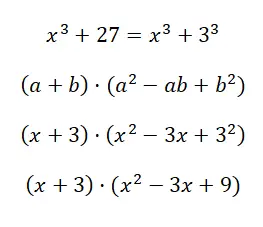
In questo caso il risultato che otteniamo è piuttosto lungo perché non può essere ulteriormente semplificato. Ma è normale arrivare a questa espressione, infatti in questi casi si può ottenere solo un risultato con la struttura equivalente al prodotto di un binomio per un trinomio, come in questo esempio.
trinomio al cubo
Il cubo di un trinomio si scrive: (a + b + c) 3 , che equivale a moltiplicare tre trinomi identici, ma senza esponente: (a + b + c) · (a + b + c) · (a + b + c). È il prodotto notevole più complesso che esista, anche se la formula è abbastanza logica e si ottiene allo stesso modo di tutti gli altri, eseguendo le moltiplicazioni corrispondenti dei polinomi. Di seguito troverai la prova della formula per questa straordinaria identità:
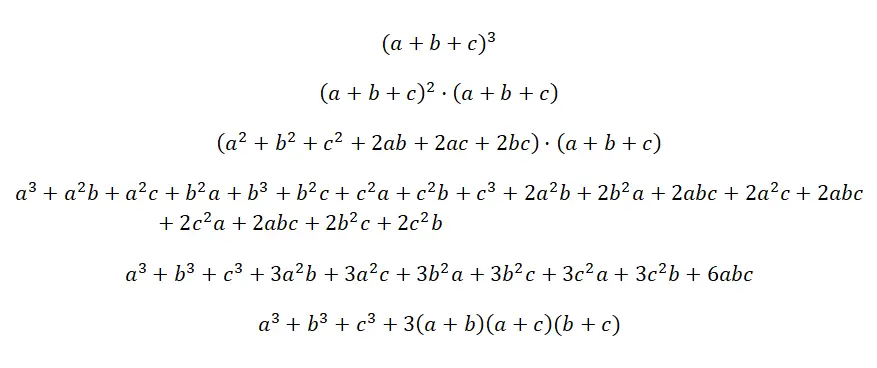
Esempio del cubo di un trinomio
Risolvi il seguente cubo trinomiale (x 2 + 3x – 4) 3 :
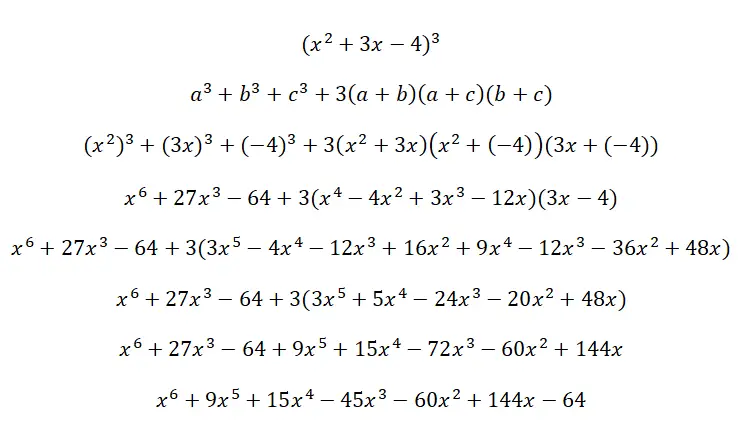
rapporti notevoli
Infine, spiegheremo i quozienti notevoli , che sono identità notevoli per risolvere rapidamente alcuni tipi di frazioni algebriche. Più precisamente, ne esistono quattro diverse tipologie, accomunate da una caratteristica: il loro risultato è formato da polinomi esatti (con resto pari a zero). Vale anche la pena ricordare che le formule dei quozienti notevoli hanno una certa relazione con le formule dei prodotti notevoli che abbiamo già spiegato.
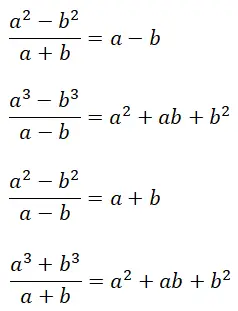
Esempio di rapporti notevoli risolti
Calcolare i seguenti rapporti notevoli:
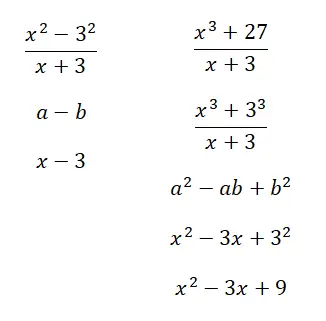
Esercizi sui prodotti notevoli risolti
Ora che sai come vengono risolti i diversi notabili, è tempo di esercitarti un po’. Per questo ti proponiamo 6 esercizi per applicare tutta la teoria spiegata. E noi ti mostriamo una tabella delle principali identità notevoli, così da averla a portata di mano mentre risolvi tutti gli esercizi:

Esercizio 1
Risolvi i quadrati binomiali (x – 4) 2 , (x + 1) 2 e (x – 3) 2 :
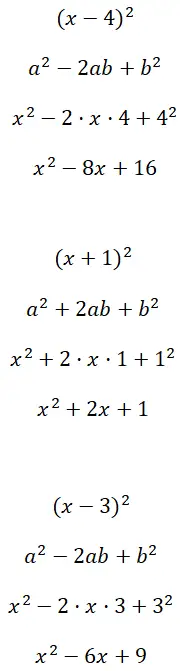
Esercizio 2
Calcola le due differenze di quadrati (x – 1) · (x + 1) e (x + 3) · (x – 3):
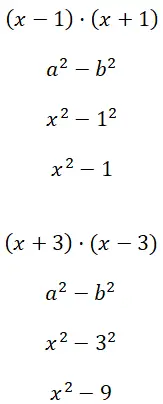
Esercizio 3
Sviluppa i prodotti notevoli nel cubo (x – 5) 3 e (x + 8) 3 :
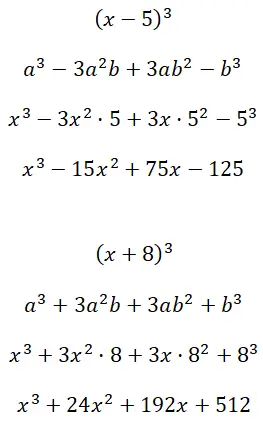
Esercizio 4
Sviluppare identità notevoli formate da termini multifattoriali (4x 2 + 5y) 2 , (5x 3 + y 2 ) · (5x 3 – y 2 ) e (5xy 2 – 2xy) 2 :
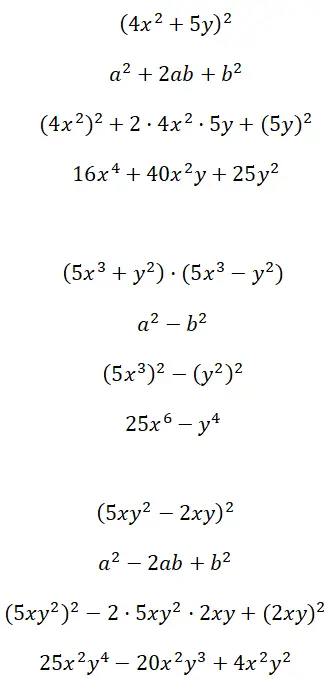
Esercizio 5
Calcolare i prodotti cubici notevoli formati dai termini multifattoriali (3x 2 + y) 3 e (5y 3 – 2x 2 ) 3 :
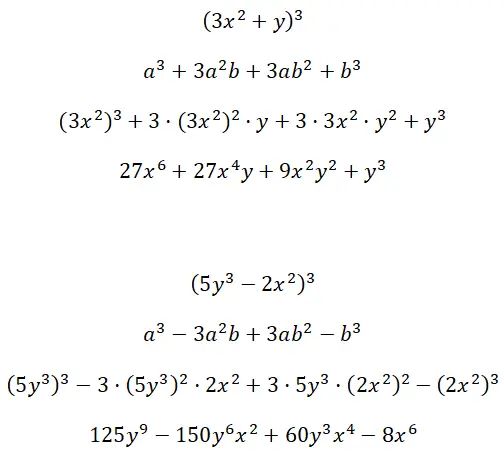
Esercizio 6
Risolvi i quadrati dei trinomi (2x 2 + 3x + 5) 2 e (3x 2 + 5x + 6):