Qui spieghiamo come i problemi di ottimizzazione delle funzioni vengono risolti in più fasi. Inoltre, potrai esercitarti con esercizi risolti su problemi di ottimizzazione.
Cosa sono i problemi di ottimizzazione?
I problemi di ottimizzazione sono problemi in cui bisogna trovare il massimo o il minimo di una funzione. Ad esempio, un problema di ottimizzazione comporterebbe il calcolo del massimo di una funzione che definisce i profitti di un’azienda.
Come risolvere i problemi di ottimizzazione
Passaggi per risolvere i problemi di ottimizzazione delle funzioni:
- Imposta la funzione che deve essere ottimizzata.
- Derivare la funzione da ottimizzare.
- Trovare i punti critici della funzione da ottimizzare. Per fare ciò, è necessario impostare la derivata della funzione uguale a zero e risolvere l’equazione risultante.
- Studiare la monotonia della funzione e determinare il massimo o il minimo della funzione.
Esempio di problema di ottimizzazione
Considerando la teoria dei problemi di ottimizzazione, risolveremo passo dopo passo un problema di questo tipo in modo che tu possa vedere come vengono svolti.
- Tra tutti i triangoli rettangoli i cui cateti misurano complessivamente 10 cm, calcola le dimensioni di quello con la superficie massima.
Per risolvere il problema chiameremo un ramo del triangolo x e l’altro ramo y :

Passaggio 1: impostare la funzione da ottimizzare.
Vogliamo che l’area del triangolo sia massima e la formula per l’area di un triangolo è:
![]()
Nel nostro caso la base del triangolo è x e la sua altezza è y . Ancora:
![]()
Abbiamo già la funzione da ottimizzare, ma dipende da due variabili mentre può dipendere solo da una. Tuttavia, la dichiarazione ci dice che le due gambe devono avere una lunghezza totale di 10 cm. Ancora:
![]()
Risolviamo y da questa equazione:
![]()
E sostituiamo l’espressione nella funzione:
![]()
![]()
Ora abbiamo la funzione di ottimizzazione pianificata e dipende solo da una variabile, quindi possiamo passare al passaggio successivo.
Passaggio 2: calcolare la derivata della funzione da ottimizzare.
È una funzione razionale, quindi applichiamo la formula della derivata della divisione per ricavarla:
![]()
![]()
Passaggio 3: trovare i punti critici.
Per trovare i punti critici della funzione, dobbiamo porre la derivata uguale a zero e risolvere l’equazione risultante:
![]()
![]()
Il 4 divide l’intero lato sinistro, quindi possiamo moltiplicarlo moltiplicando l’intero lato destro:
![]()
![]()
![]()
![]()
![]()
Passaggio 4: studiare la monotonia della funzione e determinare il massimo o il minimo della funzione.
Per studiare la monotonia della funzione rappresentiamo il punto critico che troviamo a destra:
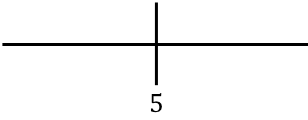
E ora valutiamo il segno della derivata in ciascun intervallo per scoprire se la funzione è crescente o decrescente. Per fare ciò, prendiamo un punto in ogni intervallo (mai il punto critico) e guardiamo quale segno ha la derivata in quel punto:
![]()
![]()
![]()
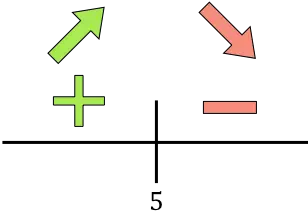
Se la derivata è positiva significa che la funzione è crescente, se la derivata è negativa significa che la funzione è decrescente. Pertanto gli intervalli per aumentare e diminuire la funzione sono:
Crescita:
![]()
Diminuire:
![]()
A x=5 la funzione passa da crescente a decrescente, quindi x=5 è un massimo relativo della funzione da ottimizzare .
Pertanto x=5 è il valore del ramo del triangolo che ha l’area massima. Basta calcolare il valore dell’altra gamba:
![]()
In conclusione i valori che massimizzano l’area massima del triangolo sono:
![]()
![]()
Problemi di ottimizzazione risolti
Problema 1
La medicina viene somministrata a una persona malata e
![]()
qualche ora dopo, la concentrazione ematica del principio attivo è data dalla funzione
![]()
milligrammi per millilitro. Determinare il valore massimo di
![]()
e indica quando tale valore viene raggiunto.
Passaggio 1: impostare la funzione da ottimizzare.
In questo problema ci danno già la funzione proposta, ovvero
![]()
Passaggio 2: calcolare la derivata della funzione da ottimizzare.
La funzione è composta dal prodotto di 2 funzioni. Pertanto, per calcolare la derivata della funzione, dobbiamo applicare la regola della derivata di un prodotto:
![]()
![]()
Passaggio 3: trovare i punti critici.
Per trovare i punti critici della funzione, risolviamo
![]()
![]()
![]()
Prendiamo il fattore comune per risolvere l’equazione:
![]()
Perché la moltiplicazione sia uguale a 0, uno dei due elementi della moltiplicazione deve essere zero. Pertanto, impostiamo ciascun fattore uguale a 0:
![Rendered by QuickLaTeX.com \displaystyle e^{-t/2}\cdot \left(1 - \frac{1}{2}t \right) = 0 \longrightarrow \begin{cases} e^{-t/2}=0 \ \bm{\times} \\[2ex]\displaystyle 1 - \frac{1}{2}t=0 \ \longrightarrow \ 1= \frac{1}{2}t \ \longrightarrow \ \bm{2=t} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8390139724dbc4ad014db2a76e508290_l3.png)
Un numero elevato a un altro numero non può mai dare 0, quindi,
![]()
Non c’è soluzione.
Passaggio 4: studiare la monotonia della funzione e determinare il massimo o il minimo della funzione.
Per studiare la monotonia della funzione rappresentiamo il punto critico che troviamo a destra:
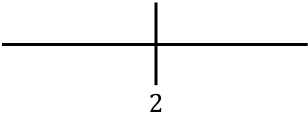
E ora valutiamo il segno della derivata in ciascun intervallo, per scoprire se la funzione è crescente o decrescente. Prendiamo quindi un punto in ogni intervallo (mai il punto critico) e guardiamo che segno ha la derivata in questo punto:
![]()
![]()
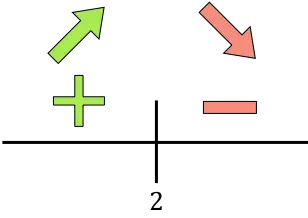
Se la derivata è positiva significa che la funzione aumenta, se invece la derivata è negativa significa che la funzione diminuisce. Pertanto gli intervalli di crescita e decremento della funzione da ottimizzare sono:
Crescita:
![]()
Diminuire:
![]()
La funzione passa da crescente a decrescente in t=2, quindi t=2 è il massimo della funzione. La concentrazione massima sarà quindi raggiunta in t=2 ore.
Infine, sostituiamo il valore in corrispondenza del quale si verifica il massimo nella funzione originale, per trovare il valore della concentrazione massima:
![]()
Problema 2
Un negozio spera di vendere 40 scooter elettrici al prezzo di 1.000 euro ciascuno. Ma secondo una ricerca di mercato, per ogni riduzione di 50 euro sul prezzo dello scooter, ci sarà un aumento delle vendite dei 10 scooter più venduti.
Per prima cosa scrivere la funzione di ricavo del negozio in base al numero di volte in cui il prezzo originale dello scooter, pari a 1.000 $, viene ridotto di 50 $. Successivamente, determina il prezzo dello scooter per ottenere il massimo profitto e le entrate guadagnate a quel prezzo.
Passaggio 1: impostare la funzione da ottimizzare.
La formulazione del problema ci fornisce un indizio, poiché ci dice che la funzione deve dipendere dal numero di volte in cui il prezzo iniziale viene ridotto di 50$. Chiameremo quindi x il numero di volte in cui il prezzo verrà ridotto di 50€:
![]()
€
La funzione del ricavo sarà il numero di scooter venduti moltiplicato per il prezzo di ciascuno scooter:
![]()
Il numero di scooter venduti sarà di 40 più 10 scooter per ogni riduzione di prezzo di 50 €. Ancora:
![]()
Il prezzo di ogni scooter sarà di 1.000 € alla partenza e diminuirà di 50 € ad ogni calo di prezzo. Ancora:
![]()
La funzione per ottimizzare il problema è quindi:
![]()
![]()
![]()
![]()
Passaggio 2: calcolare la derivata della funzione da ottimizzare.
Essendo una funzione polinomiale, la derivata è più semplice da calcolare:
![]()
Passaggio 3: trovare i punti critici della funzione.
Per trovare i punti critici della funzione, risolviamo
![]()
![]()
![]()
![]()
![]()
Passaggio 4: studiare la monotonia della funzione e determinare il massimo o il minimo della funzione.
Per studiare la monotonicità della funzione, rappresentiamo il punto critico calcolato sulla retta numerica:
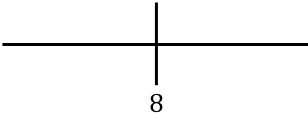
E ora valutiamo il segno della derivata in ciascun intervallo, per scoprire se la funzione è crescente o decrescente. Prendiamo quindi un punto in ogni intervallo (mai il punto critico) e guardiamo che segno ha la derivata in questo punto:
![]()
![]()
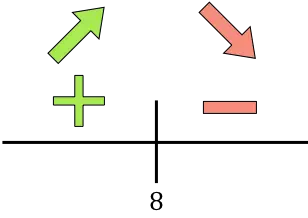
Se la derivata è positiva significa che la funzione è crescente, se la derivata è negativa significa che la funzione è decrescente. Pertanto gli intervalli di crescita e declino sono:
Crescita:
![]()
Diminuire:
![]()
La funzione passa da crescente a decrescente in x=8, quindi x=8 è il massimo della funzione. Pertanto il guadagno massimo si otterrà effettuando 8 volte la riduzione di 50€.
Sostituiamo ora il valore in corrispondenza del quale appare il reddito massimo nella funzione originale, per trovare il valore del reddito massimo:
![]()
![]()
€
E il prezzo di ogni scooter dopo aver effettuato 8 volte lo sconto di 50€ sarà:
![]()
![]()
€
Problema 3
La funzione di costo (in migliaia di euro) di un’azienda può essere determinata utilizzando la seguente espressione:
![]()
Oro
![]()
rappresenta le migliaia di unità prodotte di un dato articolo.
Determinare quanto deve essere prodotto affinché il costo sia minimo, quale sarebbe tale costo e quale sarebbe il costo se nessuno di questi articoli fosse prodotto.
Passaggio 1: impostare la funzione da ottimizzare.
La formulazione del problema ci fornisce già la funzione da ottimizzare, ovvero
![]()
Passaggio 2: calcolare la derivata della funzione da ottimizzare.
![]()
Passaggio 3: trovare i punti critici.
Per trovare i punti critici della funzione, risolviamo
![]()
![]()
![]()
![]()
![]()
Passaggio 4: studiare la monotonia della funzione e determinare il massimo o il minimo della funzione.
Rappresentiamo il punto critico che troviamo a destra:
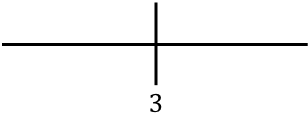
E ora valutiamo il segno della derivata in ciascun intervallo, per scoprire se la funzione è crescente o decrescente. Prendiamo quindi un punto in ogni intervallo (mai il punto critico) e guardiamo che segno ha la derivata in questo punto:
![]()
![]()
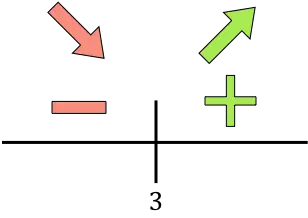
Se la derivata è maggiore di zero, la funzione aumenta in questo intervallo. Se invece la derivata è minore di zero la funzione diminuisce in questo intervallo. Pertanto gli intervalli di incremento e decremento della funzione sono:
Crescita:
![]()
Diminuire:
![]()
La funzione passa da decrescente a crescente in x=3, quindi x=3 è il minimo della funzione. Pertanto, il costo minimo sarà raggiunto producendo 3.000 unità.
Sostituiamo ora il valore al quale viene raggiunto il costo minimo nella funzione originale per trovare il valore del costo minimo:
![]()
milioni di euro.
Ci chiedono invece quale sarebbe il costo se non si producesse nulla, cioè quando
![]()
È quindi necessario calcolare
![]()
![]()
milioni di euro.
Problema 4
Vogliamo costruire una cornice rettangolare in legno che delimiti un’area di 2 m 2 . Sappiamo che il prezzo del legno è di 7,5 €/m per i lati orizzontali e di 12,5 €/m per i lati verticali. Determinare le dimensioni che deve avere il rettangolo affinché il costo totale della cornice sia il minimo possibile e che detto costo sia minimo.
Passaggio 1: impostare la funzione da ottimizzare.
Per risolvere il problema, chiameremo x il lato orizzontale e y il lato verticale :

L’acquisto del lato orizzontale costa 7,5€ mentre l’acquisto del lato verticale costa 12,5€. Inoltre, per ogni cornice abbiamo bisogno di due lati orizzontali e due lati verticali. Pertanto il costo del serramento può essere determinato con la seguente funzione:
![]()
Abbiamo già la funzione da ottimizzare. Ma dipende da due variabili quando può dipendere solo da una. Tuttavia il comunicato ci dice che la superficie del telaio deve essere di 2 m 2 . Ancora:
![]()
Eliminiamo la variabile y :
![]()
E sostituiamo l’espressione trovata nella funzione da ottimizzare:
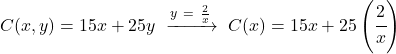
![]()
Passaggio 2: calcolare la derivata della funzione da ottimizzare.
![]()
Passaggio 3: trovare i punti critici.
Per trovare i punti critici della funzione, risolviamo
![]()
![]()
![]()
![]()
![]()
![]()
Moltiplichiamo trasversalmente per risolvere l’equazione con le frazioni:
![]()
![]()
![]()
![]()
![]()
Passaggio 4: studiare la monotonia della funzione e determinare il massimo o il minimo della funzione.
Rappresentiamo il punto critico trovato per analizzare la monotonia della funzione sulla retta:
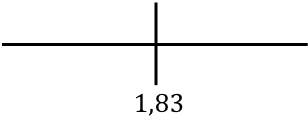
E ora valutiamo il segno della derivata in ciascun intervallo, per scoprire se la funzione è crescente o decrescente. Prendiamo quindi un punto in ogni intervallo (mai il punto critico) e guardiamo che segno ha la derivata in questo punto:
![]()
![]()
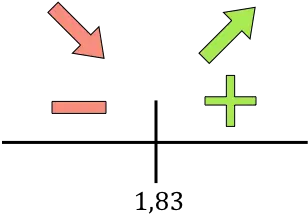
Se la derivata è positiva significa che la funzione è crescente, se la derivata è negativa significa che la funzione è decrescente. Pertanto gli intervalli di crescita e declino sono:
Crescita:
![]()
Diminuire:
![]()
La funzione cambia da decrescente ad crescente in x=1,83, quindi x=1,83 è il minimo della funzione.
Pertanto x=1,83 è il valore del lato orizzontale che rappresenta il costo minimo. Ora calcoliamo il valore del lato verticale:
![]()
Pertanto, i valori che compongono il costo quadro minimo sono:
lato orizzontale
![]()
lato verticale
![]()
E il costo minimo raggiunto con questi valori è:
![]()
€
Problema 5
La porta di una cattedrale è formata da un arco semicirconferenziale sorretto da due colonne, come mostrato nella figura seguente:
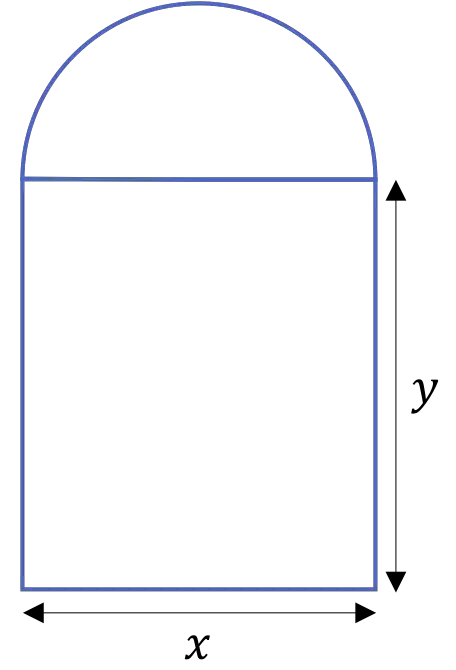
Se il perimetro della porta è di 20 m determinare le misure
![]()
E
![]()
che massimizza la superficie dell’intera porta.
Passaggio 1: impostare la funzione da ottimizzare.
L’area di un cerchio viene calcolata con la formula
![]()
Quindi l’area dell’intera porta sarà l’area del rettangolo più metà dell’area della circonferenza:
![]()
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \left(\cfrac{x}{2}\right)^2 \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-baa2e14b061cf14a657782db8fe91b92_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \cdot \cfrac{x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9196d8284edebe6450d49aa5a0b6a3e1_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y +\cfrac{1}{2} \left[ \cfrac{\pi \cdot x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-b25e1d2c661585be998d1596d6650c01_l3.png)
![]()
Abbiamo già la funzione da ottimizzare. Ma dipende da due variabili quando può dipendere solo da una.
Tuttavia dal comunicato risulta che il perimetro dell’intero cancello è di 20m. Il perimetro di un cerchio si calcola con la formula
![]()
Pertanto il perimetro dell’intera porta sarà:
![Rendered by QuickLaTeX.com P= x +2y +\cfrac{1}{2} \left[ 2 \pi \left( \cfrac{x}{2}\right) \right] = x+2y + \cfrac{2 \pi x }{2 \cdot 2} = x+2y + \cfrac{ \pi x }{2 }](https://mathority.org/wp-content/ql-cache/quicklatex.com-7709d0c72bf84a17ac83bc46f5cce002_l3.png)
Il perimetro deve essere di 20 m. Impostiamo quindi l’espressione precedente uguale a 20 per trovare la relazione tra
![]()
E
![]()
![]()
Moltiplichiamo tutti i termini per 2 per eliminare le frazioni:
![]()
![]()
Chiariamo
![]()
![]()
![]()
E sostituiamo l’espressione trovata nella funzione da ottimizzare:
![]()
![]()
![]()
Passaggio 2: calcolare la derivata della funzione da ottimizzare.
![]()
![]()
Passaggio 3: trovare i punti critici.
Per trovare i punti critici della funzione, risolviamo
![]()
![]()
![]()
Questa è un’equazione con frazioni, quindi moltiplichiamo ogni termine per i lcm dei denominatori per eliminare le frazioni:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Passaggio 4: studiare la monotonia della funzione e determinare il massimo o il minimo della funzione.
Per studiare la monotonia della funzione rappresentiamo il punto critico che troviamo a destra:
E ora valutiamo il segno della derivata in ciascun intervallo, per scoprire se la funzione è crescente o decrescente. Prendiamo quindi un punto in ogni intervallo (mai il punto critico) e guardiamo che segno ha la derivata in questo punto:
![]()
![]()
Se la derivata è positiva significa che la funzione è crescente, se la derivata è negativa significa che la funzione è decrescente. Pertanto gli intervalli di crescita e declino sono:
Crescita:
![]()
Diminuire:
![]()
La funzione passa da crescente a decrescente in x=5,6, quindi x=5,6 è il massimo della funzione.
Ancora,
![]()
è il valore che costituisce la superficie massima. Ora calcoliamo il valore di
![]()
![]()
Pertanto i valori che compongono la superficie massima sono:
![]()
![]()
Problema 6
Vogliamo costruire un serbatoio a forma di cilindro con una superficie di 54 cm 2 . Determina il raggio della base e l’altezza del cilindro in modo che il volume sia massimo.
Passaggio 1: impostare la funzione da ottimizzare.
Il volume di un cilindro si calcola con la seguente formula:
![]()
L’area della base è un cerchio, quindi lo è la sua formula
![]()
. La formula per il volume del cilindro è quindi:
![]()
Abbiamo già la funzione da ottimizzare. Ma dipende da due variabili (
![]()
E
![]()
) mentre può dipendere solo da uno. Tuttavia, l’affermazione ci dice che l’area del cilindro deve essere 54 cm 2 , quindi sfrutteremo questa condizione per trovare la relazione tra
![]()
E
![]()
Per calcolare l’area di un cilindro bisogna sommare la sua area laterale con le aree delle due basi:
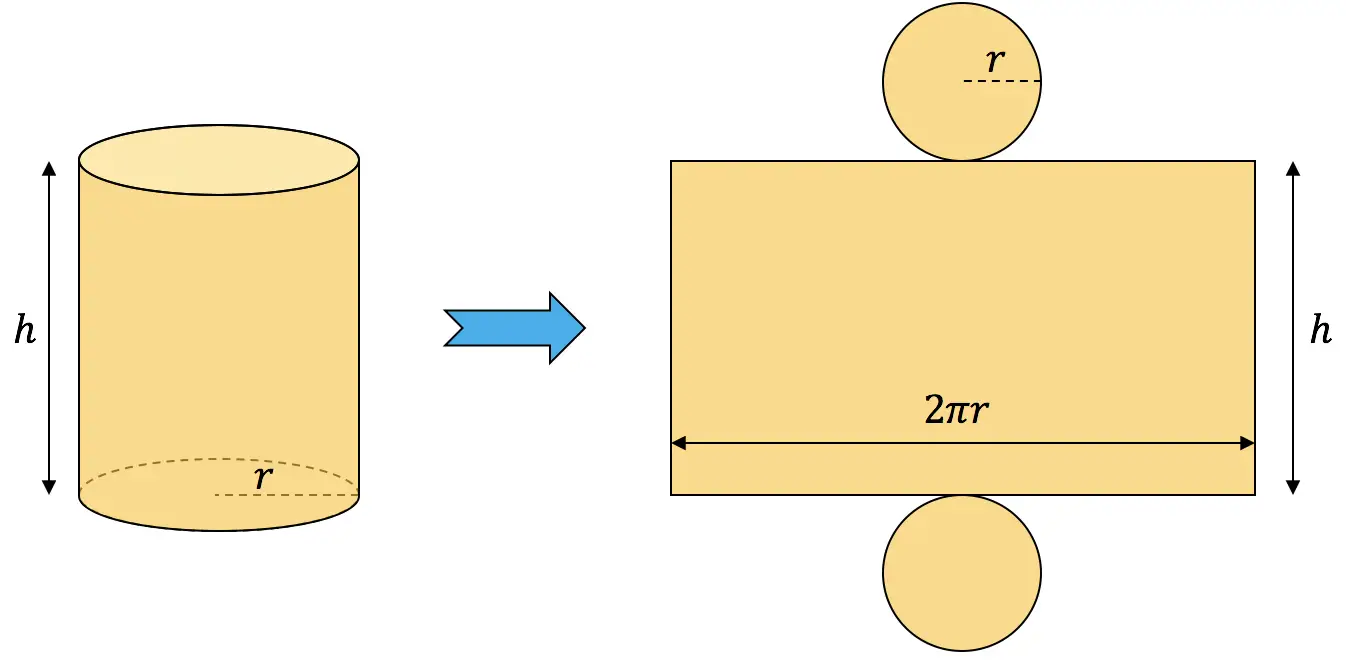
![]()
L’area del cilindro deve essere 54 cm 2 , quindi poniamo l’espressione precedente pari a 54 per ottenere il rapporto tra
![]()
E
![]()
![]()
Chiariamo
![]()
![]()
![]()
E sostituiamo l’espressione trovata nella funzione da ottimizzare:
![]()
![]()
![]()
Passaggio 2: calcolare la derivata della funzione da ottimizzare.
![]()
Passaggio 3: trovare i punti critici.
Per trovare i punti critici della funzione, risolviamo
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Passaggio 4: studiare la monotonia della funzione e determinare il massimo o il minimo della funzione.
Per studiare la monotonicità della funzione, rappresentiamo il punto critico che si trova sulla retta numerica:
E ora valutiamo il segno della derivata in ciascun intervallo, per scoprire se la funzione è crescente o decrescente. Prendiamo quindi un punto in ogni intervallo (mai il punto critico) e guardiamo che segno ha la derivata in questo punto:
![]()
![]()
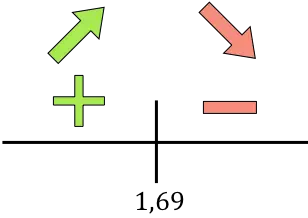
Se la derivata è positiva significa che la funzione è crescente, se la derivata è negativa significa che la funzione è decrescente. Pertanto gli intervalli di crescita e declino sono:
Crescita:
![]()
Diminuire:
![]()
La funzione passa da crescente a decrescente in r=1,69, quindi r=1,69 cm è il massimo della funzione.
Pertanto r=1,69 è il valore del raggio che costituisce il volume massimo. Ora calcoliamo l’altezza:
![]()
Quindi i valori che fanno raggiungere il volume massimo sono:
Radio
![]()
Altezza
![]()