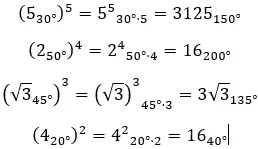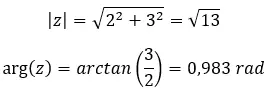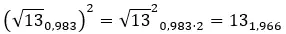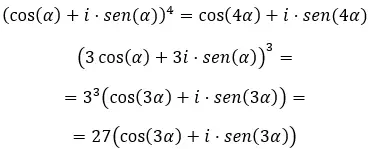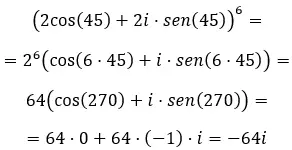Risolvere le potenze dei numeri complessi è una cosa abbastanza semplice da fare, se si conosce il metodo giusto. Pertanto, in questo articolo spiegheremo come risolvere le potenze complesse in tre modi: per i numeri complessi in forma binomiale, in forma polare e in forma trigonometrica.
Come risolvere la potenza di un numero complesso?
Come abbiamo detto nell’introduzione, quando si opera con poteri complessi si possono verificare tre situazioni. Il primo e più semplice è quando ci viene dato il numero in forma polare . Il secondo è quando ci viene dato il numero in forma binomiale e il terzo è quando ci viene dato il numero in forma trigonometrica.
In altre parole, quando si opera con complessi in forma polare, l’esercizio può essere risolto più rapidamente. Pertanto, si consiglia di convertire il numero in questione in forma polare. Ma in realtà, tutti i metodi sono facili da risolvere . Detto questo, ti spiegheremo come si risolvono tutti i casi e ti proporremo un esercizio.
Potenze dei numeri complessi in forma polare
Quando vogliamo risolvere potenze complesse in forma polare , eleviamo semplicemente il modulo a qualsiasi e moltiplichiamo l’argomento per n. Espressa matematicamente, otteniamo la seguente formula:
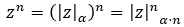
Ecco alcuni esempi, così puoi provare a risolverli da solo:
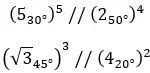
Potenze dei numeri complessi in forma binomiale
Quando invece vogliamo risolvere potenze complesse in forma binomiale possiamo utilizzare due metodi diversi. La prima si occupa di risolvere la potenza in modo “algebrico” (risolvendo come se fossi una variabile). E il secondo sistema consiste nel convertire la forma binomiale in polare e quindi seguire la procedura precedente.
Se non sai come passare dalla forma binomiale a quella polare, te lo spieghiamo molto chiaramente nel nostro articolo sui numeri complessi . Anche se ora lo vedremo rapidamente con un esempio.
Prova a risolvere la seguente potenza complessa: (2 + 3i) 2 .
Potenze dei numeri complessi in forma trigonometrica
Infine, quando vogliamo risolvere potenze complesse in forma trigonometrica , dobbiamo utilizzare la nota formula di de Moivre. Che è scritto così:
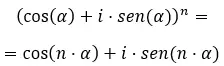
Conoscendo questa formula, prova a risolvere i seguenti esercizi:

Ulteriori informazioni sui poteri complessi
- Numeri complessi
- Proprietà dei complessi
- Operazioni su numeri complessi
- radici complesse