Posizioni relative di una retta e di un piano

In questa pagina troverai le posizioni relative di una linea e di un piano. Ti spieghiamo come si calcola la posizione relativa tra una linea e un piano (2 metodi) e, inoltre, potrai vedere esempi ed esercizi risolti passo dopo passo.

Quali sono le posizioni relative tra una linea e un piano?

Prima di esaminare tutte le possibili posizioni relative tra una linea e un piano, dobbiamo ovviamente sapere cosa sono le linee e cos’è un piano . Quindi se ancora non hai ben chiari questi due concetti ti consigliamo di dare prima un’occhiata alle pagine collegate dove viene spiegato nel dettaglio.

Pertanto, nella geometria analitica, ci sono solo tre posizioni relative nello spazio tra una linea e un piano:

Retta contenuta nel piano : quando la retta è contenuta nel piano significa che hanno un numero infinito di punti in comune.
Retta e piano paralleli : Una retta e un piano sono paralleli quando non hanno punti in comune.
Intersezione di linea e piano : una linea e un piano si intersecano quando la linea interseca il piano in un punto. Quindi hanno solo una cosa in comune.

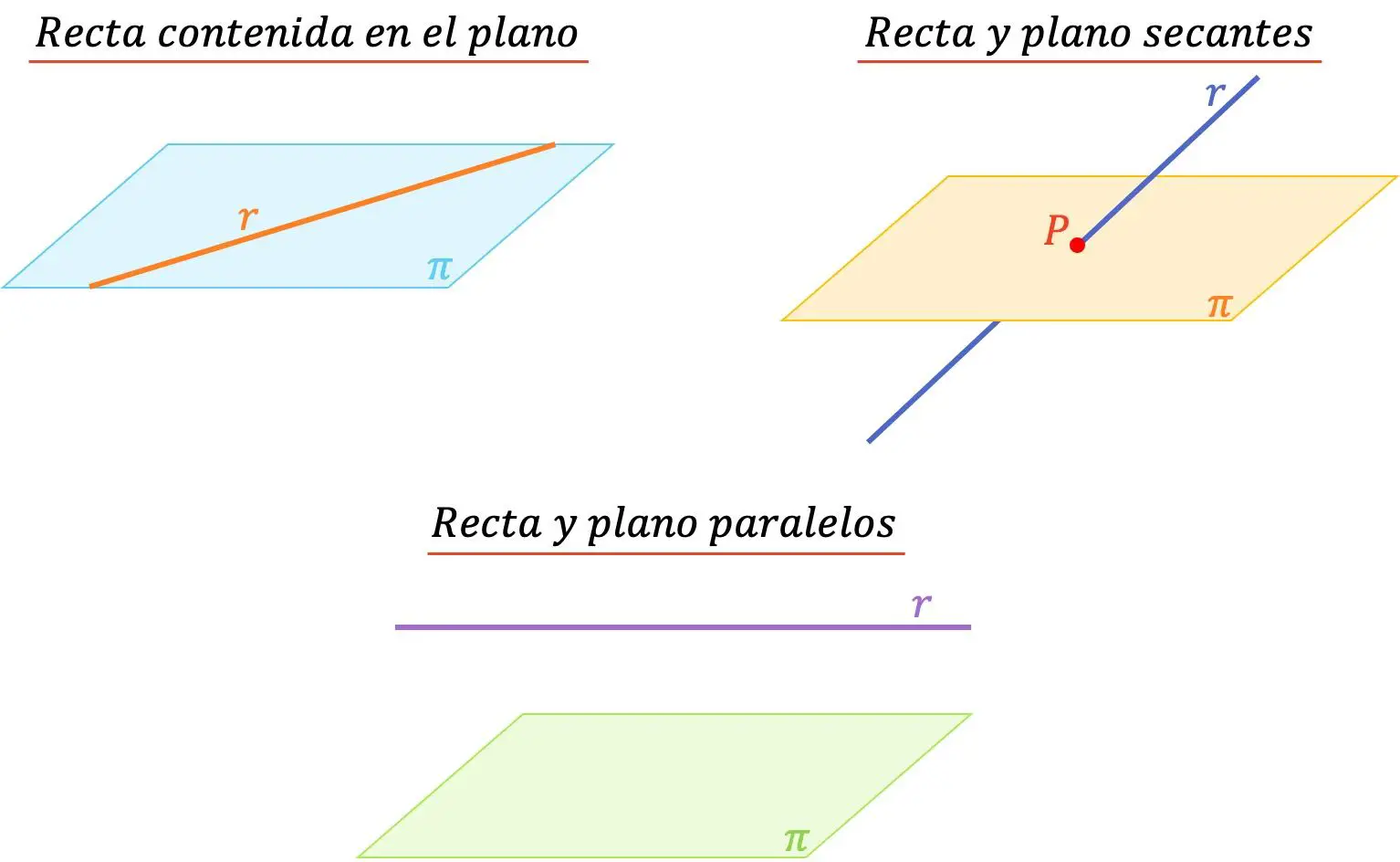
Quando invece la linea è contenuta nel piano o quando sono parallele tra loro, l’angolo che formeranno sarà 0º. D’altra parte, quando la linea e il piano si intersecano, l’angolo tra i due elementi geometrici può variare da 0º (non compreso) a 90º (compreso).

Come calcolare la posizione relativa di una linea e di un piano?

Esistono principalmente due metodi per trovare la posizione relativa tra una linea e un piano nello spazio: per intervalli o per vettori .

Quando la linea è espressa come un’equazione implicita (o generale), è più semplice utilizzare il metodo dei ranghi. Se invece la retta è data con un altro tipo di equazione, ad esempio quando è sotto forma di equazione vettoriale, parametrica o continua, è più veloce utilizzare il metodo vettoriale.

Se non ricordi come sono le equazioni della retta, ti lasciamo una pagina dove puoi consultare tutte le equazioni della retta . Qui troverai tutte le equazioni della retta, una formula per trovare velocemente l’equazione di una retta passante per due punti, esempi ed esercizi risolti passo dopo passo.

Pertanto è più pratico utilizzare un metodo o un altro a seconda del problema, per questo motivo ti consigliamo di sapere come eseguire entrambe le procedure. Di seguito è riportata la spiegazione di entrambi i metodi con esempi.

Quando la linea ha la forma di un’equazione implicita (o generale).

Un modo per determinare la posizione relativa tra una linea e un piano è calcolare il rango di due matrici.

Se la linea è definita dalle sue equazioni implicite (o generali):

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0\end{cases}$

E il piano è espresso anche sotto forma di un’equazione generale:

$\pi : \ A_3x+B_3y+C_3z+D_3=0$

Chiameremo A la matrice composta dai coefficienti A, B e C delle equazioni del piano e della retta:

$\displaystyle A =\begin{pmatrix} A_1&B_1&C_1\\[1.1ex] A_2&B_2&C_2\\[1.1ex] A_3&B_3&C_3\end{pmatrix}$

E la matrice A’ sarà la matrice espansa con tutti i coefficienti delle due equazioni:

$\displaystyle A' =\begin{pmatrix} A_1&B_1&C_1&D_1\\[1.1ex] A_2&B_2&C_2&D_2\\[1.1ex] A_3&B_3&C_3&D_3\end{pmatrix}$

Quindi, la posizione relativa tra la linea e il piano è determinata dal valore dell’estensione delle due matrici precedenti secondo la seguente tabella:

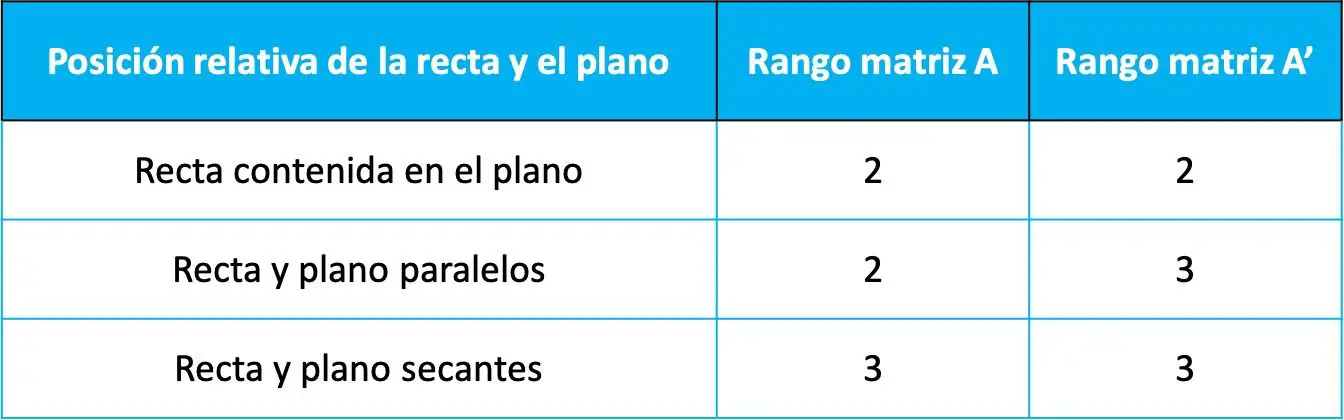
studiare la posizione relativa tra una linea e un piano nello spazio per intervalli

Che le posizioni relative dipendano dai ranghi di queste due matrici può essere dimostrato dal toerem di Rouche-Frobenius (un teorema utilizzato per risolvere sistemi di equazioni lineari). Tuttavia in questa pagina non faremo la dimostrazione perché non è necessario conoscerla e non fornisce nemmeno molto.

Esempio di come trovare la posizione relativa di una linea e di un piano in base agli intervalli

Affinché tu possa vedere esattamente come si fa, risolveremo un esercizio come esempio:

Studiare la posizione relativa tra la seguente linea e il seguente piano:

$\displaystyle r: \ \begin{cases}2x+y+z+3=0 \\[2ex] 4x-y+5z+2=0\end{cases}$

$\pi : \ 2x+2y-6=0$

La linea è definita da due piani che si intersecano, cioè è espressa come un’equazione implicita. Pertanto, utilizzeremo il metodo dei ranghi per studiare la posizione relativa tra la linea e il piano.

La prima cosa da fare è costruire la matrice A e la matrice estesa A’ con i coefficienti delle equazioni:

$\displaystyle A =\begin{pmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{pmatrix} \qquad \qquad A' =\begin{pmatrix} 2&1&1&3\\[1.1ex] 4&-1&5&2\\[1.1ex] 2&2&0&-6\end{pmatrix}$

E ora dobbiamo calcolare il rango di ciascuna matrice. Troviamo innanzitutto l’estensione della matrice A mediante determinanti:

$rg(A) = \ ?$

$\displaystyle \begin{vmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{vmatrix} =0$

$\displaystyle \begin{vmatrix} 2&1\\[1.1ex] 4&-1\end{vmatrix} =-6 \neq 0$

$rg(A) = 2$

Il determinante della matrice A è zero ma contiene una sottomatrice 2×2 il cui determinante è diverso da zero, quindi è una matrice di rango 2.

D’altra parte è necessario calcolare anche il rango della matrice A’. E l’intervallo della matrice estesa A’ sarà sempre almeno uguale a quello della matrice A, quindi dobbiamo solo verificare se è di rango 3 o 2:

$rg(A') = \ ?$

$\displaystyle \begin{vmatrix} 2&1&3\\[1.1ex] 4&-1&2\\[1.1ex] 2&2&-6\end{vmatrix} =62 \neq 0$

$rg(A') = 3$

D’altra parte, la matrice estesa A’ ha un sottodeterminante 3×3 diverso da 0, è quindi di rango 3.

Quindi, poiché la matrice A è di rango 2 e la matrice A’ è di rango 3, la linea e il piano sono paralleli .

Quando la linea ha la forma di un altro tipo di equazione

Quando la retta è espressa da un’equazione diversa da quella implicita, sia essa vettoriale, parametrica o continua, è preferibile utilizzare il metodo che spieghiamo di seguito.

Quindi, se la retta si presenta sotto forma di equazione vettoriale, di equazioni parametriche o di equazione continua, significa che conosciamo un punto che appartiene alla retta e anche il suo vettore direzione.

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r \\[2ex] P\end{cases}$

D’altra parte, sappiamo anche qual è il vettore normale (o perpendicolare) al piano:

$\vv{n} \perp \pi$

Quindi, dai 2 vettori e dal punto della linea, la posizione relativa tra la linea e il piano può essere calcolata come segue:

Se il prodotto scalare tra il vettore direzione della retta e il vettore normale al piano è diverso da zero significa che la retta è secante al piano.

$\vv{\text{v}}_r\cdot \vv{n} \neq 0 \ \color{orange}\longrightarrow \color{black} \ \text{recta y plano secantes}$
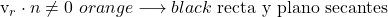
Ma se il prodotto scalare tra il vettore direzione della retta e il vettore normale al piano è uguale a zero, ci sono due possibilità: la retta è contenuta nel piano oppure sono parallele. E per sapere di quale caso si tratta, dobbiamo sostituire nell’equazione del piano le coordinate di un punto sulla retta.
- Se il punto soddisfa l’equazione del piano, la retta è contenuta nel piano.
- Se invece il punto non soddisfa l’equazione del piano, la retta e il piano sono paralleli.

Esempio di determinazione della posizione relativa di una linea e di un piano utilizzando i vettori

Una volta vista la teoria di questo metodo, vediamo ora un esercizio risolto passo dopo passo:

Trova la posizione relativa tra la seguente linea e il seguente piano:

$\displaystyle r: \ \begin{cases}x=2-3t \\[1.7ex] y=-1+2t \\[1.7ex] z=-2t\end{cases}$

$\pi : \ 2x+y-2z-3=0$

Innanzitutto, la linea è definita come equazioni parametriche, quindi il suo vettore direzione e il punto attraverso il quale passa sono:

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(-3,2,-2) \\[2ex] P(2,-1,0) \end{cases}$

E, d’altra parte, il vettore normale al piano è:

$\vv{n} =(2,1,-2)$

Una volta conosciuto il vettore direzione della retta e il vettore normale al piano, dobbiamo calcolare il prodotto scalare tra i due:

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (-3,2,-2) \cdot (2,1,-2) \\[2ex] & = -3 \cdot 2+2 \cdot 1 -2\cdot (-2) \\[2ex] &= -6 +2 +4 \\[2ex] & = 0\end{aligned}$

Il risultato del prodotto scalare è zero, quindi la linea può essere contenuta solo nel piano o essere parallela ad esso. Quindi, per scoprire di quale caso si tratta, sostituiamo le coordinate cartesiane del punto sulla retta nell’equazione del piano:

$2x+y-2z-3=0 \ \xrightarrow{P(2,-1,0)} \ 2\cdot 2 -1 -2 \cdot 0 -3 = 0$

$4- 1 -0 -3 = 0$

$0 = 0$

Sostituendo il punto della retta nell’equazione del piano otteniamo un’uguaglianza, quindi il punto rispetta l’equazione del piano e, di conseguenza, la retta è contenuta nel piano .