Questa pagina spiega le diverse posizioni relative che esistono tra una linea e un cerchio. Inoltre, sarai in grado di vedere come trovare la posizione relativa tra una linea e un cerchio.
Quali sono le posizioni relative di una linea e di un cerchio?
Nella geometria analitica, la posizione relativa di una linea rispetto ad un cerchio può essere solo esterna, tangente o secante:
- Esterno : quando la distanza tra la linea e il centro del cerchio è maggiore del raggio.
- Tangente : quando la distanza tra la linea e il centro del cerchio è uguale al raggio.
- Secante : quando la distanza tra la linea e il centro del cerchio è inferiore al raggio.
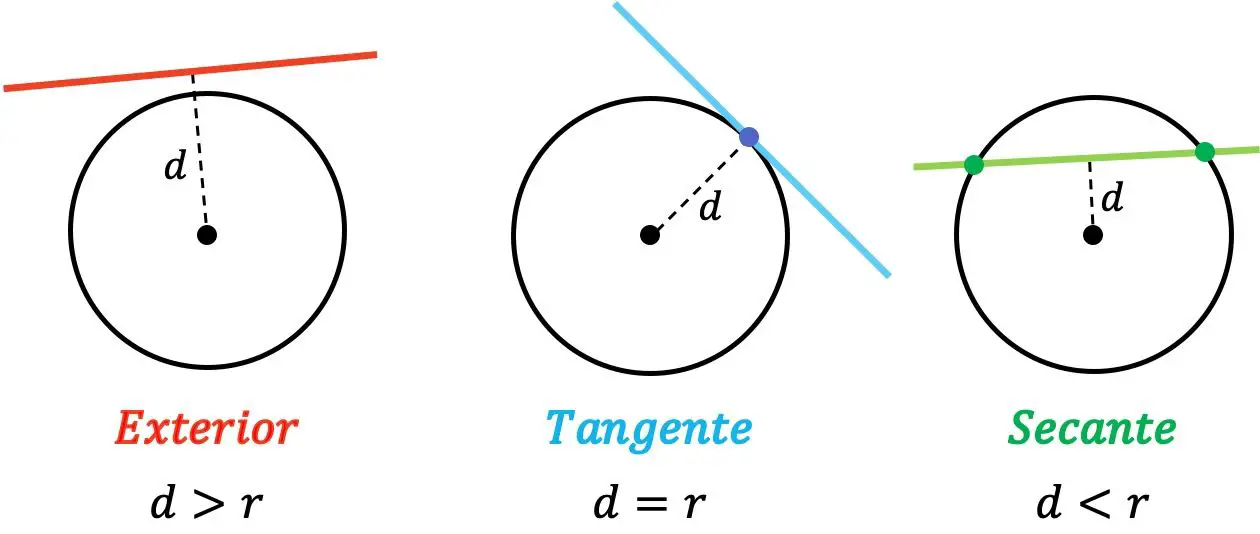
Quindi, se una linea è esterna a un cerchio, non lo interseca in nessun punto. Quando invece la retta è tangente al cerchio, i due hanno un punto in comune. Infine, una linea è secante a un cerchio quando lo interseca in due punti diversi.
Come determinare la posizione relativa tra una linea e un cerchio?
Esistono due modi per trovare la posizione relativa di una linea rispetto a un cerchio nel piano: uno calcolando la distanza tra la linea e il centro del cerchio, e l’altro risolvendo un sistema composto di equazioni dell’equazione di la retta e l’equazione della circonferenza.
Successivamente, vedremo esattamente cos’è ciascun metodo.
Metodo 1: Distanza tra la linea e il centro del cerchio
Come abbiamo visto nella spiegazione del concetto di posizione relativa tra una linea e un cerchio, la distanza tra una linea e il centro di un cerchio indica di che tipo di posizione relativa si tratta.
Questo metodo consiste quindi nel trovare la distanza tra la linea ed il centro del cerchio. Ovviamente per poterlo fare devi sapere come calcolare la distanza tra un punto e una linea , in questa pagina puoi vedere come farlo, oltre ad esempi ed esercizi risolti per esercitarti.
Quindi, a seconda del risultato della distanza ottenuta, sarà un caso o l’altro:
- La linea sarà esterna al cerchio se la distanza ottenuta è maggiore del raggio del cerchio.
- La linea sarà tangente al cerchio se la distanza ottenuta è equivalente al raggio del cerchio.
- La linea intersecherà il cerchio se la distanza ottenuta è inferiore al raggio del cerchio.
Metodo 2: risolvere un sistema di equazioni
Un altro modo per trovare la posizione relativa di una linea rispetto a un cerchio è utilizzare un sistema di equazioni formato dall’equazione della linea e dall’equazione del cerchio. Ovviamente per applicare questo metodo è necessario sapere qual è l’equazione della circonferenza e qual è la formula per l’equazione della retta .
A seconda del numero di soluzioni del sistema di equazioni, ci troveremo di fronte ad un caso o ad un altro:
- Se il sistema di equazioni non ha soluzione, significa che la retta e il cerchio non hanno un punto in comune, quindi la retta è esterna al cerchio.
- Se il sistema di equazioni ha 1 soluzione, ciò implica che la retta e il cerchio hanno un punto in comune, quindi la retta è tangente al cerchio.
- Se il sistema di equazioni ha 2 soluzioni, significa che la retta e la circonferenza hanno due punti in comune, quindi la retta è secante alla circonferenza.