Posizione relativa di due linee nello spazio

Qui troverai tutte le posizioni relative di due linee nello spazio (in R3). Inoltre, spiega come trovare la posizione relativa tra due linee utilizzando i 2 metodi possibili: per intervalli o da un punto e un vettore di ciascuna linea. Potrai anche vedere esempi ed esercizi risolti passo dopo passo.

Quali sono le posizioni relative di due linee nello spazio?

Nella geometria analitica, quando si lavora in uno spazio tridimensionale (in R3) ci sono 4 possibili posizioni relative tra due linee: due linee possono essere linee che si uniscono , linee parallele , linee secanti o linee secanti .

Linee parallele

posizione relativa di due rette parallele

Due rette sono parallele se hanno la stessa direzione ma non hanno un punto in comune. Inoltre, le linee parallele sono sempre alla stessa distanza l’una dall’altra.

linee coincidenti

Due rette coincidono se hanno la stessa direzione e, inoltre, se tutti i loro punti sono comuni.

linee che si intersecano

Due linee che si intersecano hanno direzioni diverse ma si toccano in un punto.

Linee di intersezione

Due linee che si intersecano hanno direzioni diverse e non si intersecano in nessun punto. Pertanto due linee incrociate non sono sullo stesso piano. Ad esempio, nella rappresentazione grafica sopra la linea

$s$

è sempre in anticipo

$r$

, quindi non si toccheranno mai.

Esistono 2 modi per sapere qual è la posizione relativa tra due linee, poiché dipendono da come sono espresse le equazioni delle due linee:

Se le linee sono in forma vettoriale, parametrica o di equazione continua, è meglio calcolare la posizione relativa da un punto e un vettore di ciascuna linea (la spiegazione di questo metodo è fornita di seguito).
D’altra parte, se le linee sono definite sotto forma di equazioni implicite (o generali), è più semplice conoscere la posizione relativa tra le due linee calcolando il rango di due matrici (vedi spiegazione sotto).

Determinazione della posizione relativa di due linee da un punto e un vettore

Puoi trovare quale posizione relativa c’è tra due linee con un punto e un vettore di ciascuna linea. Questo metodo è appropriato da utilizzare quando le linee sono definite sotto forma di un’equazione vettoriale, di equazioni parametriche o di un’equazione continua.

Pertanto, sia il vettore direzione e qualsiasi punto su ciascuna delle due linee:

$\displaystyle r: \ \begin{cases} \vv{\text{v}} = (\text{v}}_x, \text{v}}_y,\text{v}}_z})\\[2ex] P(P_x,P_y,P_z)\end{cases} \qquad\qquad s: \ \begin{cases} \vv{\text{v}}' = (\text{v}}_x', \text{v}}_y',\text{v}}_z'})\\[2ex] P'(P_x',P_y',P_z')\end{cases}$

Quindi, per trovare la posizione relativa di due linee, dobbiamo seguire la seguente procedura:

‣ La prima cosa che dobbiamo fare è vedere se i vettori delle due rette sono proporzionali o meno e, a seconda dei casi, facciamo quanto segue:

Se i due vettori sono proporzionali le rette possono essere parallele o coincidere. Dobbiamo quindi verificare se il punto di una retta soddisfa l’equazione dell’altra retta:
- Se il punto di una retta soddisfa l’equazione dell’altra retta, significa che le due rette coincidono.
- Altrimenti implica che le due rette siano parallele.
Se i due vettori non sono proporzionali, le linee possono intersecarsi o intersecarsi. In questo caso dobbiamo risolvere il seguente determinante 3×3:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$
- Se il determinante precedente è uguale a zero, le due rette si intersecano in un punto (si intersecano).
- Se il determinante precedente è diverso da zero le due rette si intersecano.

Il seguente grafico riassume l’intera procedura:

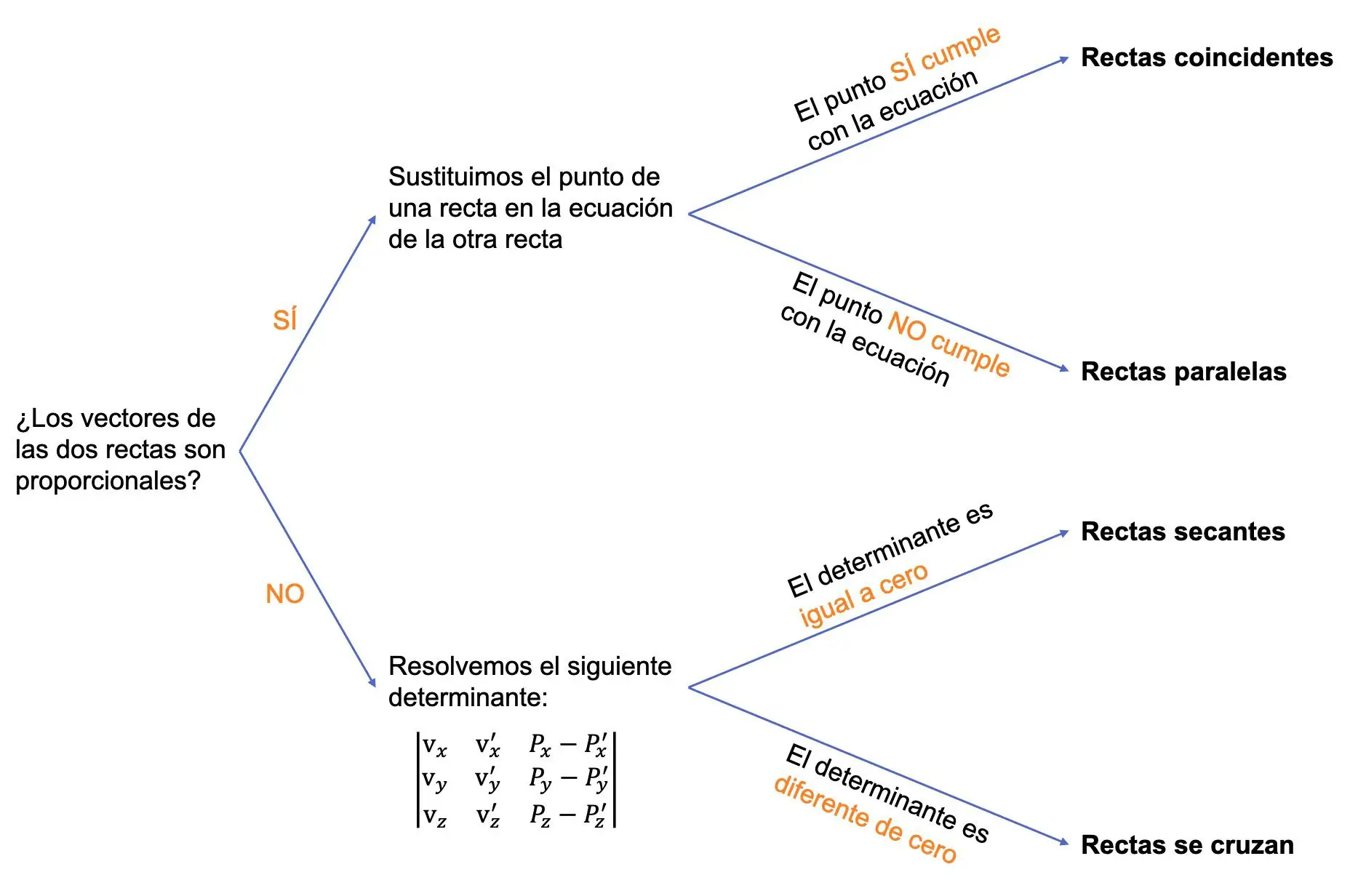
Esempio di determinazione della posizione relativa tra due linee

La procedura precedente può sembrare un po’ complicata, ma affinché tu possa vedere che è il contrario, risolveremo un problema a titolo di esempio:

Determinare la posizione relativa tra le due linee seguenti:

$r: \ (x,y,z)=(2,0,1)+t(4,-1,1)$

$s: \ (x,y,z)=(1,-3,1)+t(1,2,0)$

Le due linee sono espresse come un’equazione vettoriale, con la quale il vettore direzione di ciascuna linea è:

$\vv{r} =(4,-1,1) \qquad \qquad \vv{s}=(1,2,0)$

E un punto attraverso il quale passa ciascuna linea è:

$R(2,0,1)\qquad \qquad S(1,-3,1)$

Una volta conosciuto un punto e il vettore direzione di ciascuna retta, applichiamo il metodo visto sopra. Innanzitutto dobbiamo verificare se le coordinate dei vettori sono proporzionali:

$\cfrac{4}{1} \neq \cfrac{-1}{2} \neq \cfrac{1}{0} \quad \longrightarrow \quad \text{No proporcionales}$

Poiché i due vettori non sono proporzionali tra loro, le linee possono solo toccarsi o incrociarsi. Pertanto, ora dobbiamo risolvere il seguente determinante formato dal vettore direzione e da un punto su ciascuna linea:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

Sostituiamo i valori nella formula:

$\begin{vmatrix} 4 & 1 & 2-1 \\[1.1ex] -1 & 2 & 0-(-3) \\[1.1ex]1& 0 & 1-1 \end{vmatrix}$

E calcoliamo il determinante, per questo puoi utilizzare qualsiasi metodo (regola di Sarrus, metodo dei complementi o dei cofattori, ecc.):

$\begin{vmatrix} 4 & 1 & 1 \\[1.1ex] -1 & 2 & 3 \\[1.1ex]1& 0 & 0 \end{vmatrix} = 1$

Se il risultato della determinazione fosse stato zero, ciò significherebbe che le linee si incrociano (si toccano). Ma il determinante è diverso da 0, quindi le linee si intersecano .

Trova la posizione relativa di due linee per righe

Un altro modo per trovare la posizione relativa di due righe è calcolare i ranghi di due matrici concrete, come vedremo in seguito. Questo metodo è molto utile quando le due linee sono nella forma di un’equazione implicita (o generale).

Quindi, se abbiamo due linee espresse con le loro equazioni implicite (o generali) in uno spazio tridimensionale (in R3):

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

Sia A la matrice composta dai coefficienti delle due rette:

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

E data la matrice estesa A’, che è la matrice formata da tutti i parametri delle due linee:

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

Quindi, la posizione relativa delle due righe può essere determinata dall’intervallo delle due matrici precedenti secondo la seguente tabella:

posizioni relative di due righe per righe

Pertanto per trovare la posizione relativa tra due righe dovremo calcolare i ranghi delle due matrici e a seconda del rango di ciascuna matrice sarà l’uno o l’altro caso.

Questo teorema può essere dimostrato utilizzando il teorema di Rouché-Frobenius (un metodo utilizzato per risolvere sistemi di equazioni lineari), tuttavia in questa pagina non faremo la dimostrazione perché è piuttosto macchinosa e non aggiunge molto.

Esempio di come trovare la posizione relativa di due linee in base agli intervalli

Una volta vista la teoria sulle posizioni relative tra due righe per righe, vediamo come viene messa in pratica attraverso un esempio:

Trova la posizione relativa delle seguenti due linee:

$\displaystyle r: \ \begin{cases}3x+2y+z+4=0 \\[2ex] 4x+2z+2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}3x+4z-1=0 \\[2ex] x-5y-2z-2=0 \end{cases}$

Le due linee sono sotto forma di equazioni generali (o implicite), quindi utilizzeremo il metodo dei ranghi per trovare la posizione relativa tra le due linee. Costruiamo quindi la matrice A e la matrice estesa A’ con i coefficienti delle rette:

$\displaystyle A=\begin{pmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{pmatrix}$

Una volta che abbiamo entrambe le matrici, dobbiamo calcolare il rango di ciascuna. Per prima cosa calcoliamo il rango della matrice A in base ai determinanti:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4 \end{vmatrix} = -20 \bm{\neq 0}$

$rg(A)=3$

La matrice A contiene il determinante di una sottomatrice 3×3 diversa da zero, quindi la matrice A ha rango 3 .

E ora calcoliamo l’ambito della matrice estesa A’. La matrice A’ sarà sempre almeno al rango della matrice A, che in questo caso vale 3, quindi basta verificare se è di rango 4 o di rango 3. Per fare questo risolviamo il determinante della matrice 4× 4 per addizioni (o cofattori):

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{vmatrix} =$

$\displaystyle =3 \cdot\begin{vmatrix} 0 & 2&2\\[1.1ex] 0 & 4&-1\\[1.1ex] -5 & -2 &-2 \end{vmatrix}-2\cdot\begin{vmatrix}4 & 2&2\\[1.1ex]3 & 4&-1\\[1.1ex]1 & -2 &-2 \end{vmatrix}+1\cdot\begin{vmatrix}4 & 0 &2\\[1.1ex]3 & 0 & -1\\[1.1ex]1 & -5 & -2 \end{vmatrix}-4\cdot \begin{vmatrix}4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{vmatrix}$

$\displaystyle =3 \cdot 50-2\cdot(-50)+1\cdot(-50)-4\cdot 50$

$\displaystyle =150+100-50-200$

$\displaystyle \bm{=0}$

$rg(A')=3$

Il determinante dell’intera matrice estesa è zero, quindi anche la matrice A’ è di rango 3 .

Quindi la matrice A e la matrice A’ sono di rango 3 quindi, di conseguenza, le due rette si intersecano . Cioè, c’è solo un punto di intersezione tra loro.

$\color{orange} \boxed{\color{black} \quad rg(A) = rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Secantes} \quad \vphantom{\Bigl(}}$

Ricorda che hai sopra una tabella che riassume tutti i possibili casi di posizioni relative tra due linee secondo gli intervalli delle matrici A e A’.

Risolti problemi di posizione relativa tra due linee nello spazio

Esercizio 1

Trova la posizione relativa tra le due linee seguenti:

$r: \ (x,y,z)=(3,4,0)+t(2,1,-3)$

$s: \ (x,y,z)=(1,-2,2)+t(0,5,1)$

vedi soluzione

Poiché entrambe le linee sono espresse come un’equazione vettoriale, troveremo la posizione relativa tra le due linee dal metodo di un punto e di un vettore di ciascuna linea.

Il vettore direzione di ciascuna linea è:

$\vv{r} =(2,1,-3) \qquad \qquad \vv{s}=(0,5,1)$

E un punto che appartiene a ciascuna linea è:

$R(3,4,0)\qquad \qquad S(1,-2,2)$

Pertanto, per applicare la procedura, è necessario prima verificare se le componenti dei vettori di direzione sono proporzionali:

$\cfrac{2}{0} \neq \cfrac{1}{5} \neq \cfrac{-3}{1} \quad \longrightarrow \quad \text{No proporcionales}$

Poiché i due vettori non sono proporzionali tra loro, le linee possono solo intersecarsi o intersecarsi. Pertanto, ora dobbiamo risolvere il seguente determinante costituito dal vettore direzione e da un punto su ciascuna linea:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

Sostituiamo i valori nella formula:

$\begin{vmatrix} 2 & 0 & 3-1 \\[1.1ex] 1 & 5 & 4-(-2) \\[1.1ex]-3& 1 & 0-2 \end{vmatrix}$

E calcoliamo il determinante:

$\begin{vmatrix} 2 & 0 & 2 \\[1.1ex] 1 & 5 & 6 \\[1.1ex]-3& 1 & -2 \end{vmatrix}= 0$

Il risultato del determinante è equivalente a 0, quindi le linee si intersecano .

Esercizio 2

Calcolare la posizione relativa delle due linee seguenti:

$\displaystyle r: \ \begin{cases} x=3+2t \\[1.7ex] y=1+3t \\[1.7ex] z=2-t \end{cases} \qquad \qquad s: \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

vedi soluzione

La prima linea è sotto forma di equazioni parametriche e la seconda linea è sotto forma di un’equazione continua, con la quale determineremo la posizione relativa tra le due linee dal metodo del vettore a un punto di ciascuna linea.

Le coordinate del vettore direzione destra

$r$

sono i coefficienti davanti al parametro

$t,$

e le coordinate del vettore direzione della linea

$s$

sono i numeri dei denominatori:

$\vv{r} =(2,3,-1) \qquad \qquad \vv{s}=(-4,-6,2)$

E un punto che appartiene a ciascuna linea è:

$R(3,1,2)\qquad \qquad S(-1,-5,4)$

Pertanto, per applicare la procedura, è necessario prima verificare se le componenti dei vettori di direzione sono proporzionali:

$\cfrac{2}{-4} = \cfrac{3}{-6}= \cfrac{-1}{2} \quad \longrightarrow \quad \text{Proporcionales}$

I due vettori sono proporzionali tra loro, quindi le rette possono essere solo parallele o coincidenti. Per togliere questo dubbio è necessario sostituire il punto sulla retta

$r$

nell’equazione della retta

$s$

(o viceversa) per vedere se soddisfa detta equazione:

$R(3,1,2) \ \longrightarrow \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

$\cfrac{3+1}{-4}=\cfrac{1+5}{-6} = \cfrac{2-4}{2}$

$\cfrac{4}{-4}=\cfrac{6}{-6} = \cfrac{-2}{2}$

$-1=-1 = -1$

Sostituendo il punto sulla retta otteniamo un’uguaglianza, per cui il punto di una retta soddisfa l’equazione dell’altra retta e, inoltre, i loro vettori di direzione sono proporzionali. Pertanto le due linee coincidono.

Esercizio 3

Trova la posizione relativa delle seguenti due linee:

$\displaystyle r: \ \begin{cases}2x-2y-2z+5=0 \\[2ex] 2x-y-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}4x-y+2z+3=0 \\[2ex] x-2y-3z+6=0 \end{cases}$

vedi soluzione

Le due linee sono in forma di equazione generale (o implicita), quindi utilizzeremo il metodo dei ranghi per trovare la posizione relativa tra le due linee. Realizziamo quindi la matrice A e la matrice espansa A’ con i coefficienti delle rette:

$\displaystyle A=\begin{pmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3\end{pmatrix} \qquad \qquad A'=\begin{pmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{pmatrix}$

Una volta che abbiamo entrambe le matrici, dobbiamo calcolare il rango di ciascuna. Per prima cosa calcoliamo il rango della matrice A in base ai determinanti:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 \\[1.1ex]2 & -1 \end{vmatrix}=2 \neq 0$

$rg(A)=2$

Tutti i determinanti 3×3 della matrice A sono zero, ma all’interno della matrice c’è un determinante 2×2 diverso da zero, quindi la matrice A ha rango 2 .

E ora calcoliamo l’ambito della matrice estesa A’. La matrice A’ sarà sempre almeno l’intervallo della matrice A, che in questo caso è 2, quindi occorre verificare se ha un determinante 3×3 che non si annulla e anche quanto vale il determinante della intera matrice:

$rg(A')= \ ?$

$\displaystyle \displaystyle \begin{vmatrix}2 & -2 & 5\\[1.1ex]2 & -1 &-1\\[1.1ex]4 & -1 &3\end{vmatrix}=22 \neq 0$

$\displaystyle det(A')=\begin{vmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{vmatrix}=0$

$rg(A')=3$

La matrice estesa A’ contiene infatti 3×3 sottodeterminanti diversi da zero e, inoltre, il determinante dell’intera matrice estesa è uguale a 0, quindi la matrice A’ ha rango 3 .

Quindi la matrice A è di rango 2 e la matrice A’ è di rango 3, quindi le due rette sono parallele . Vale a dire, non hanno nulla in comune.

$\color{orange} \boxed{\color{black} \quad rg(A) = 2 \neq rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Paralelas} \quad \vphantom{\Bigl(}}$

Ricorda che nella spiegazione del metodo (sopra) hai una tabella che riassume tutti i possibili casi di posizioni relative tra due linee secondo i ranghi delle matrici A e A’.

Esercizio 4

Trova la posizione relativa delle seguenti due linee:

$\displaystyle r: \ \begin{cases}4x-y+2z=0 \\[2ex] x+y+3z-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}2x+5y-z-2=0 \\[2ex] 2x+3z+1=0 \end{cases}$

vedi soluzione

In questo caso, le due linee sono in forma di equazione cartesiana (o implicita), quindi utilizzeremo il metodo di ordinamento per trovare la posizione relativa tra le due linee. Costruiamo quindi la matrice A e la matrice estesa A’ con i coefficienti delle rette:

$\displaystyle A=\begin{pmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{pmatrix}$

Una volta conosciute le due matrici, dobbiamo calcolare il rango di ciascuna. Per prima cosa calcoleremo il rango della matrice A in base ai determinanti:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1 \end{vmatrix} = -65 \bm{\neq 0}$

$rg(A)=3$

La matrice A contiene una sottomatrice 3×3 il cui determinante è diverso da zero, quindi la matrice A ha rango 3 .

E ora calcoliamo l’ambito della matrice estesa A’. La matrice A’ sarà sempre almeno di rango della matrice A, che in questo caso vale 3, per cui basta verificare se è di rango 4 o di rango 3. Per fare questo risolviamo il determinante di l’insieme della matrice 4×4 per addizioni (o cofattori):

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{vmatrix} =$

$\displaystyle =4 \cdot\begin{vmatrix} 1 & 3&-1\\[1.1ex] 5 & -1&-2\\[1.1ex] 0 & 3 &1 \end{vmatrix}-(-1)\cdot\begin{vmatrix}1 & 3&-1\\[1.1ex]2 & -1 & -2\\[1.1ex]2 & 3 &1 \end{vmatrix}+2\cdot\begin{vmatrix}1 & 1 &-1\\[1.1ex]2 & 5 & -2\\[1.1ex]2 & 0 &1 \end{vmatrix}-0\cdot \begin{vmatrix}1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{vmatrix}$

$\displaystyle =4 \cdot(-25)+1\cdot(-21)+2\cdot 9$

$\displaystyle =-100-21+18$

$\displaystyle =-103\bm{\neq0}$

$rg(A')=4$

Il determinante dell’intera matrice estesa è diverso da zero, quindi la matrice A’ ha rango 4 .

Dunque che la matrice A è di rango 3 e che invece la matrice A’ è di rango 4, quindi le due rette si intersecano in un punto.

$\color{orange} \boxed{\color{black} \quad rg(A) = 3 \neq rg(A')= 4 \quad \longrightarrow \quad \text{Rectas se cruzan} \quad \vphantom{\Bigl(}}$

Ricorda che nella spiegazione della procedura (sopra) hai una tabella dove ci sono tutti i possibili casi di posizioni relative tra due linee secondo i ranghi delle matrici A e A’.

Quali sono le posizioni relative di due linee nello spazio?

Determinazione della posizione relativa di due linee da un punto e un vettore

Esempio di determinazione della posizione relativa tra due linee

Trova la posizione relativa di due linee per righe

Esempio di come trovare la posizione relativa di due linee in base agli intervalli

Risolti problemi di posizione relativa tra due linee nello spazio

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Lascia un commento Annulla risposta