In questa pagina troverai la spiegazione dei diversi metodi esistenti per determinare la posizione relativa di due linee nel piano (in R2). Inoltre, vedrai diversi esempi e potrai esercitarti con esercizi risolti passo dopo passo.
Qual è la posizione relativa di due linee nel piano?
Prima di guardare le posizioni relative tra due linee nel piano, ovviamente devi sapere esattamente cos’è una linea, lo puoi trovare nella definizione di linea .
Pertanto, quando si lavora in due dimensioni (in R2), ci sono 3 tipi di possibili posizioni relative tra due linee:
linee che si intersecano

Due rette che si intersecano hanno un solo punto in comune.
Linee parallele

Due rette sono parallele se non hanno un punto in comune. Cioè, se non si incrociano mai.
linee coincidenti

Due rette sono uguali se tutti i loro punti sono comuni.
D’altra parte, l’angolo tra due linee nel piano dipende anche dalla loro posizione relativa:
- Le linee che si intersecano si intersecano con un angolo compreso tra 0º (non incluso) e 90º (incluso). Inoltre, se formano solo un angolo retto di 90º, significa che le due linee sono perpendicolari.
- Le linee parallele formano un angolo di 0º poiché hanno la stessa direzione.
- E, per lo stesso motivo, anche le linee coincidenti formano tra loro un angolo di 0º.
Se vuoi sapere come viene calcolato l’angolo tra due linee, puoi controllare la formula dell’angolo tra due linee . Qui troverai una spiegazione dettagliata su come determinare l’angolo tra due linee, oltre a diversi esempi e persino esercizi risolti in modo da poter esercitarti e comprendere appieno il concetto.
Come trovare la posizione relativa di due linee nel piano
Conoscere la posizione relativa tra due linee nello spazio bidimensionale dipende da come le linee sono espresse:
- Vettori di direzione della linea: se due linee hanno un vettore di direzione diverso, devono intersecarsi. Se invece le coordinate dei loro vettori di direzione sono uguali o proporzionali, possono essere paralleli o coincidere (è necessario verificare se hanno un punto in comune).
- Equazione esplicita: quando due rette hanno pendenze diverse
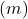
si seccano al contrario se le linee hanno la stessa pendenza ma un diverso ordine all’origine
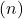
sono paralleli. Infine, due rette si confondono quando originariamente hanno pendenze e ordinate uguali.
- Equazione generale (o implicita): due rette con coefficienti non proporzionali A e B si intersecheranno sempre. Tuttavia, saranno parallele quando questi due parametri saranno proporzionali tra loro ma non al coefficiente C. E, infine, quando i tre termini saranno proporzionali, ciò implica che le rette si confondono.
Se hai dubbi sulle equazioni della retta sopra, puoi consultare la spiegazione delle equazioni della retta nel piano . Qui troverai la formula di tutte le equazioni di linea, come si calcolano, esempi ed esercizi risolti di equazioni di linea.
Nella tabella seguente si ha un riepilogo delle proprietà precedenti:

Successivamente, vedremo due esempi di come determinare la posizione relativa tra due linee:
Esempio 1
- Trova la posizione relativa tra le seguenti due linee definite sotto forma di un’equazione esplicita:
![]()
Le due rette hanno la stessa pendenza:
![]()
Ma all’origine hanno computer diversi:
![]()
Quindi, avendo la stessa pendenza ma intercettazioni diverse, le rette sono parallele .
Esempio 2
- Determina la posizione relativa tra le seguenti due linee espresse con la loro equazione implicita (o generale):
![]()
Entrambe le rette sono espresse come un’equazione esplicita, quindi dobbiamo vedere se qualcuno dei loro coefficienti è proporzionale:
![]()
I 3 termini delle rette sono proporzionali, quindi le rette coincidono .
Determina la posizione relativa di due linee nel piano con un sistema di equazioni
Un altro modo per conoscere la posizione relativa tra due linee è analizzare il sistema di equazioni formato dalle equazioni delle linee:
- Se il sistema ha un’unica soluzione , le linee si intersecano. Inoltre il punto di intersezione delle due rette è la soluzione del sistema.
- Se si tratta di un sistema senza soluzione , ciò indica che le rette non hanno punti in comune e, quindi, sono rette parallele.
- Se il sistema ha infinite soluzioni , ciò significa che le rette hanno tutti i punti in comune e, quindi, sono rette che si intersecano.
Esempio 3
- Calcola la posizione relativa delle seguenti due linee utilizzando un sistema di equazioni:
![]()
Per trovare la posizione relativa delle due linee, dobbiamo risolvere il seguente sistema di equazioni lineari formate dalle due linee:
![Rendered by QuickLaTeX.com \left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-243b1e787e6532fbafbfca53d934f4ad_l3.png)
In questo caso risolveremo il sistema con il metodo di sostituzione. Isoleremo quindi la variabile
![]()
dalla seconda equazione e sostituitela nella prima equazione:
![Rendered by QuickLaTeX.com \left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\} \begin{array}{l} \\[2ex] \longrightarrow \ y=3-5x \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ad3456c92c838f40d60afdb45e1eb2f3_l3.png)
![]()
![]()
![]()
![]()
![]()
E una volta che sapremo quanto vale l’ignoto
![]()
Sostituiamo il suo valore nell’espressione trovata per
![]()
![]()
![]()
Abbiamo quindi ottenuto una sola soluzione del sistema di equazioni composto dalle due rette, quindi le due rette si intersecano . E il punto in cui si intersecano è la soluzione del sistema, cioè il punto
![]()
Risolti problemi di posizione relativa di due linee nel piano
Esercizio 1
Determina se le seguenti rette si intersecano, sono parallele o coincidono:
![]()
Entrambe le rette sono espresse come un’equazione implicita (o generale), quindi dobbiamo vedere se qualcuno dei loro coefficienti è proporzionale:
![]()
Solo i coefficienti A e B delle rette sono proporzionali tra loro, e non al coefficiente C. Pertanto le due rette sono parallele .
Esercizio 2
Trova la posizione relativa tra le seguenti due linee espresse come equazioni parametriche:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=4-5t \\[2ex] y= 1+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=-2t \\[2ex] y=6+9t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bafb951a2141722b0bbb7a1681f506ea_l3.png)
Potremmo risolvere il sistema di equazioni formato dalle due linee per trovare la loro posizione relativa. Tuttavia, poiché sono sotto forma di equazioni parametriche, si possono facilmente trovare i loro vettori di direzione e se non sono proporzionali significa che le linee si intersecano. E in questo caso non dedicheremo molto tempo alla risoluzione di un intero sistema di equazioni.
In modo che le coordinate cartesiane del vettore di direzione di ciascuna linea siano i numeri davanti al parametro
![]()
![]()
Una volta conosciuti i vettori di direzione, controlliamo la loro proporzionalità:
![]()
I vettori di direzione non sono proporzionali, quindi le linee si incrociano .
Esercizio 3
Indica se le seguenti linee si intersecano, sono parallele o coincidenti e trova anche un punto di intersezione tra loro (se applicabile).
![]()
Le due rette sono definite dalla loro equazione esplicita e hanno pendenze diverse:
![]()
Poiché hanno pendenze diverse, le linee si intersecano .
Pertanto, poiché le rette si intersecano, avranno 1 punto in comune e per calcolarlo dobbiamo risolvere il sistema di equazioni formato dalle due rette:
![Rendered by QuickLaTeX.com \left.\begin{array}{l} y=4x-5\\[2ex] y=-2x+7\end{array}\right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b3923ff74a214543ddd2cc44a42e3813_l3.png)
In questo caso risolveremo il sistema con il metodo dell’equalizzazione perché entrambi
![]()
sono già cancellati:
![]()
![]()
![]()
![]()
![]()
E una volta che abbiamo l’ignoto
![]()
sostituiamo il suo valore in qualsiasi espressione di
![]()
per scoprire quanto vale:
![]()
![]()
Quindi il punto di intersezione delle due rette è il risultato del sistema:
![]()
Esercizio 4
Calcolare il valore delle incognite
![]()
E
![]()
in modo che le due rette seguenti siano parallele:
![]()
Le linee sono descritte in forma di equazione generale (o implicita). Pertanto, affinché le due rette siano parallele, i loro coefficienti A e B devono essere proporzionali, ovvero deve essere soddisfatta la seguente equazione:
![]()
Dobbiamo quindi risolvere l’equazione precedente per ottenere il valore dell’incognita
![]()
Per fare ciò, moltiplichiamo le frazioni trasversalmente:
![]()
![]()
![]()
D’altra parte, affinché le rette siano parallele i loro termini indipendenti non possono essere proporzionali agli altri coefficienti:
![]()
Pertanto, come prima, risolviamo la disuguaglianza moltiplicando trasversalmente le frazioni:
![]()
![]()
![]()
Insomma, in modo che le due rette siano parallele
![]()
deve essere 2 e
![]()
può essere qualsiasi numero reale tranne 3.
Esercizio 5
Trova l’equazione esplicita della retta parallela alla retta
![]()
e cosa succede oltre questo punto
![]()
essere sincero
![]()
![]()
In modo che la linea sia parallela alla linea
![]()
entrambi devono avere la stessa pendenza. e la pendenza della linea
![]()
è 2:
![]()
Pertanto l’equazione della retta da trovare sarà:
![]()
E una volta che conosciamo la pendenza della retta, possiamo calcolare l’intercetta y sostituendo il punto che appartiene alla retta nell’equazione della retta:
![]()
![]()
![]()
![]()
![]()
Quindi l’equazione esplicita della retta è:
![]()
Se sei arrivato fin qui, significa che hai già padroneggiato le posizioni relative tra due linee nel piano. Ben fatto!
Ma una cosa che molti si chiedono è… a che serve conoscere la posizione relativa tra due linee?
Ebbene, una delle applicazioni della posizione relativa tra linee è poter conoscere la distanza tra 2 linee, poiché il calcolo della distanza tra due linee dipende dalla loro posizione relativa:
- Se le linee si intersecano o coincidono, la distanza è zero.
- Quando invece le rette sono parallele occorre applicare una formula specifica. Se sei più interessato, puoi controllare come viene calcolata la distanza tra due linee parallele .