Piani perpendicolari

In questa pagina troverai cosa sono i piani perpendicolari, come determinare se due piani sono perpendicolari, come calcolare un piano perpendicolare, esempi ed esercizi risolti di piani perpendicolari,…

Cosa sono due piani perpendicolari?

Nella geometria analitica, due piani sono perpendicolari quando si intersecano ad angolo retto (90º).

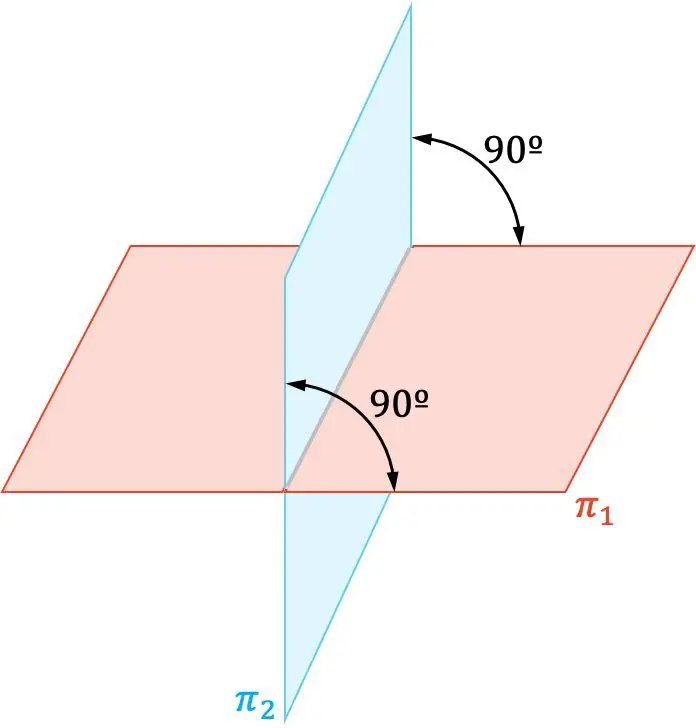
Inoltre, anche i vettori normali di due piani perpendicolari sono ortogonali tra loro.

Ovviamente la distanza tra due piani perpendicolari è sempre zero, perché si intersecano in una linea. Anche se sembra molto semplice, il concetto di distanza tra due piani è molto importante, quindi ti consigliamo di visitare il link se hai domande a riguardo.

D’altra parte, due piani posizionati perpendicolarmente non sono l’unica posizione relativa possibile tra piani, poiché due piani nello spazio (in R3) possono anche essere intersecanti, paralleli o coincidenti.

Come fai a sapere se un piano è perpendicolare a un altro?

Una volta vista la definizione di piani perpendicolari, vediamo come sapere se due piani sono perpendicolari o meno:

Due piani sono perpendicolari quando i loro vettori normali sono perpendicolari. Pertanto, per determinare se due piani sono perpendicolari tra loro, dobbiamo calcolare l’angolo formato dai loro vettori normali, e se questi formano un angolo di 90º, ciò significa che i piani sono perpendicolari.

Quindi per trovare la perpendicolarità di due piani bisogna sapere come calcolare l’angolo formato da due vettori . Se non ricordi come si fa, puoi consultare il link, dove troverai la nostra spiegazione oltre alla formula necessaria per determinare l’angolo tra due vettori. Inoltre, potrai vedere esempi ed esercitarti con esercizi risolti.

Ma in breve, due vettori sono perpendicolari quando il loro prodotto scalare è zero. Pertanto, due piani saranno perpendicolari quando il prodotto scalare dei vettori normali associati è 0.

Esempio di due piani perpendicolari

Ad esempio, controlliamo se i seguenti due piani sono perpendicolari:

$\pi_1 : \ 3x-4y+2z+5 =0$

$\pi_2 : \ 2x+5y+7z-6 =0$

Le coordinate X, Y, Z del vettore normale ad un piano coincidono con i coefficienti A, B, C della sua equazione generale (o implicita). Pertanto, il vettore normale a ciascun piano è:

$\vv{n}_1 =(3,-4,2)$

$\vv{n}_2 =(2,5,7)$

E ora controlliamo se si tratta di due piani perpendicolari calcolando il prodotto scalare tra i loro vettori normali:

$\begin{aligned} \vv{n}_1 \cdot \vv{n}_2 & = (3,-4,2)\cdot (2,5,7) \\[2ex] & = 3 \cdot 2 +(-4) \cdot 5 +2 \cdot 7 \\[2ex] &=6-20+14 \\[2ex] &\bm{= 0}\end{aligned}$

Il prodotto scalare tra i due vettori normali è 0, quindi i due piani sono perpendicolari tra loro.

Calcolare un piano perpendicolare ad una linea in un punto

Un tipico problema di piani e rette consiste nel trovare l’equazione di un piano perpendicolare ad una retta in un dato punto. Quindi, di seguito vedremo come si risolve mediante un esempio:

Trova l’equazione del piano perpendicolare alla retta.
$r$

Di

$P,$

detto dritto e punto:

$\displaystyle r: \ \begin{cases} x=3-2t \\[1.7ex] y=-1+4t \\[1.7ex] z=1+t \end{cases} \qquad \qquad P(1,3,-2)$

Per prima cosa dobbiamo trovare il vettore normale al piano in questione. e come la linea retta

$r$

è perpendicolare al piano, il suo vettore normale coinciderà con il vettore direzione della retta.

In questo caso, la linea

$r$

è sotto forma di equazioni parametriche, quindi le componenti del suo vettore di direzione sono i termini che precedono il parametro

$t:$

$\vv{r} =(-2,4,1)$

Pertanto, il vettore normale al piano sarà lo stesso del vettore direzione della linea:

$\vv{n} =(-2,4,1)$

E, quindi, l’equazione implicita (o generale) del piano sarà la seguente:

$\pi : \ -2x+4y+1z+D=0$

È quindi sufficiente determinare il valore del coefficiente D. Per fare ciò, sostituiamo nella sua equazione le coordinate del punto la cui affermazione ci dice che appartiene al piano:

$P(1,3,-2)$

$-2\cdot 1+4\cdot 3-2+D=0$

$-2+12-2+D=0$

$8+D=0$

$D=-8$

In breve l’equazione cartesiana del piano è:

$\bm{\pi : \ -2x+4y+z-8=0}$

Se invece vuoi praticare altri esercizi sulla perpendicolarità tra oggetti geometrici, puoi visitare la nostra pagina sulle linee perpendicolari. Troverai tutto quello che c’è da sapere sulle rette perpendicolari : quando due rette sono perpendicolari, come calcolare una perpendicolare all’altra, esempi, esercizi risolti e molto altro.

Proprietà dei piani perpendicolari

Tutti i piani perpendicolari hanno le seguenti caratteristiche:

Relazione simmetrica : se un piano è perpendicolare ad un altro piano, anche questo piano è perpendicolare al primo piano. Questa proprietà è posseduta anche dai piani paralleli.

$\pi_1 \bm{\perp} \pi_2 \ \longrightarrow \ \pi_2 \bm{\perp} \pi_1$

Proprietà non riflessiva : ovviamente nessun piano può essere perpendicolare a se stesso.

$\pi_1 \ \cancel{\bm{\perp}}} \ \pi_1$

Teorema: nello spazio tridimensionale (3D), qualsiasi coppia di piani perpendicolari a un terzo piano deve necessariamente essere parallela. In altre parole, se un piano è perpendicolare ad un altro piano e questo piano è anche perpendicolare ad un terzo piano, il primo e l’ultimo piano sono paralleli tra loro.

Cosa sono due piani perpendicolari?

Come fai a sapere se un piano è perpendicolare a un altro?

Esempio di due piani perpendicolari

Calcolare un piano perpendicolare ad una linea in un punto

Proprietà dei piani perpendicolari

Lascia un commento Annulla risposta