Piani paralleli - Mathority

In questa pagina troverai tutto sui piani paralleli: quando due piani sono paralleli, le equazioni di due piani paralleli, esempi, esercizi risolti, proprietà,…

Cosa sono due piani paralleli?

Nella geometria analitica due piani sono paralleli quando sono sempre alla stessa distanza. Pertanto due piani paralleli non si intersecano mai e non hanno nulla in comune.

Due piani posizionati paralleli non sono l’unica posizione relativa possibile tra piani, poiché due piani nello spazio (in R3) possono anche essere intersecanti o coincidenti.

Come fai a sapere se due piani sono paralleli?

Dopo aver visto la definizione di piani paralleli, vediamo come si può determinare se due piani sono paralleli oppure no.

Partendo dall’equazione generale (o implicita) di due piani diversi:

$\pi_1 : \ A_1x+B_1y+C_1z+D_1 =0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2 =0$

I 2 piani saranno paralleli se i loro coefficienti A, B e C sono proporzionali tra loro e non al coefficiente D. In altre parole, il parallelismo tra due piani si verifica quando è soddisfatta la seguente equazione:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white ]}]{equation*} \cfrac{A_1}{A_2}=\cfrac{B_1}{B_2} = \cfrac{C_1}{C_2}\neq \cfrac{D_1}{D_2} \end{empheq}$

Esempio di due piani paralleli

Ad esempio, i seguenti due piani sono paralleli:

$\pi_1 : \ 6x+2y-4z+1 =0$

$\pi_2 : \ 3x+y-2z+5 =0$

I piani sono paralleli perché i coefficienti delle variabili X, Y, Z sono proporzionali tra loro, ma non ai termini indipendenti:

$\cfrac{6}{3} =\cfrac{2}{1} =\cfrac{-4}{-2} \neq \cfrac{1}{5} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

Calcola la distanza tra due piani paralleli

Due piani paralleli sono sempre alla stessa distanza, quindi, per trovare la distanza tra due piani paralleli, possiamo prendere un punto su uno dei due piani e calcolare la distanza da quel punto all’altro piano. Pertanto, per calcolare la distanza tra 2 piani paralleli, è necessario conoscere la formula per la distanza da un punto a un piano .

È un metodo per trovare la distanza tra due piani paralleli. Esiste però un modo ancora più semplice per farlo quando i coefficienti A, B e C delle equazioni dei due piani coincidono:

Considera le equazioni generali (o implicite) di due piani paralleli:

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

La formula per calcolare la distanza tra due piani paralleli è:

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

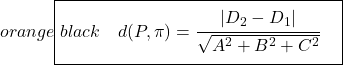
Quindi sicuramente è più semplice trovare la distanza tra due piani paralleli utilizzando la formula poiché si tratta solo di applicare la formula e basta, ma dipende dal problema. Inoltre, riteniamo che sia meglio spiegare entrambi i modi di calcolo della distanza in modo che tu possa scegliere quello che preferisci.

Esempio di calcolo della distanza tra due piani paralleli

Ad esempio, calcoleremo la distanza tra i seguenti due piani:

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

Dobbiamo innanzitutto verificare che abbiamo a che fare con due piani paralleli. Pertanto, tutti i coefficienti delle equazioni piane sono proporzionali tranne i termini indipendenti, quindi sono effettivamente due piani paralleli.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

In questo caso i termini A, B e C delle equazioni dei due piani non coincidono, ma possiamo ottenere questo risultato dividendo per due l’intera equazione del secondo piano:

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

Quindi, le equazioni dei due piani ora hanno gli stessi coefficienti A, B e C. Pertanto possiamo facilmente calcolare la distanza tra i due piani con la formula per la distanza tra due piani paralleli:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Sostituiamo i valori e risolviamo le operazioni:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

Cosicché la distanza tra un piano e l’altro piano è uguale all’unità.

Proprietà dei piani paralleli

Le caratteristiche dei piani paralleli sono le seguenti:

Proprietà riflessiva : ogni piano è parallelo a se stesso.

$\pi_1 \parallel \pi_1$

Proprietà simmetrica : se un piano è parallelo a un altro, anche questo piano è parallelo al primo. Questa proprietà è posseduta anche dai piani perpendicolari.

$\pi_1 \parallel \pi_2 \ \longrightarrow \ \pi_2 \parallel \pi_1$

Proprietà transitiva : se un piano è parallelo ad un altro piano, e questo secondo piano è parallelo ad un terzo piano, anche il primo piano è parallelo al terzo piano.

$\left. \begin{array}{c} \pi_1 \parallel \pi_2\\[2ex] \pi_2 \parallel \pi_3 \end{array} \right\} \longrightarrow \ \pi_1 \parallel \pi_3$