In questo articolo spieghiamo cos’è la periodicità di una funzione. Inoltre, vedrai diversi esempi di funzioni periodiche. Infine, analizzeremo il periodo delle funzioni trigonometriche, poiché è una delle sue caratteristiche più importanti.
Qual è la periodicità di una funzione?
La periodicità di una funzione è una caratteristica delle funzioni che ripetono ciclicamente i loro valori, ovvero una funzione è periodica se il suo grafico si ripete ad ogni determinato intervallo. Questo intervallo è chiamato periodo.
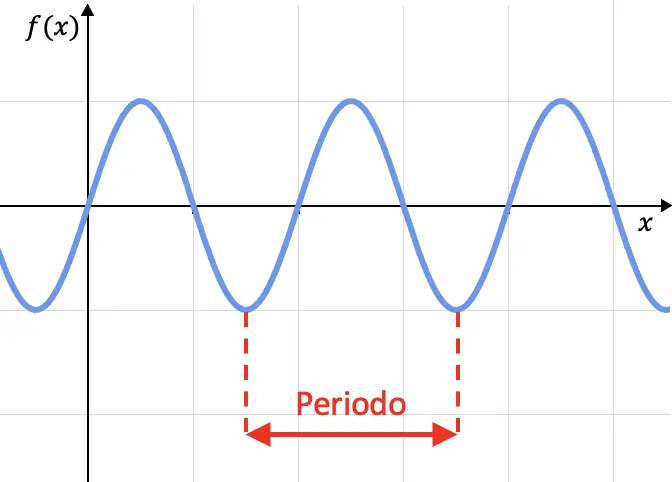
Matematicamente una funzione è definita periodica se è soddisfatta solo
![]()
per qualsiasi valore della variabile indipendente x.
![]()
Dove T è il periodo della funzione periodica ik intero.
Esempi di periodicità di funzioni
Una volta visto il concetto di periodicità di una funzione, vedremo diversi esempi su come calcolare la periodicità di una funzione.
Esempio 1
Determina se la seguente funzione è periodica:
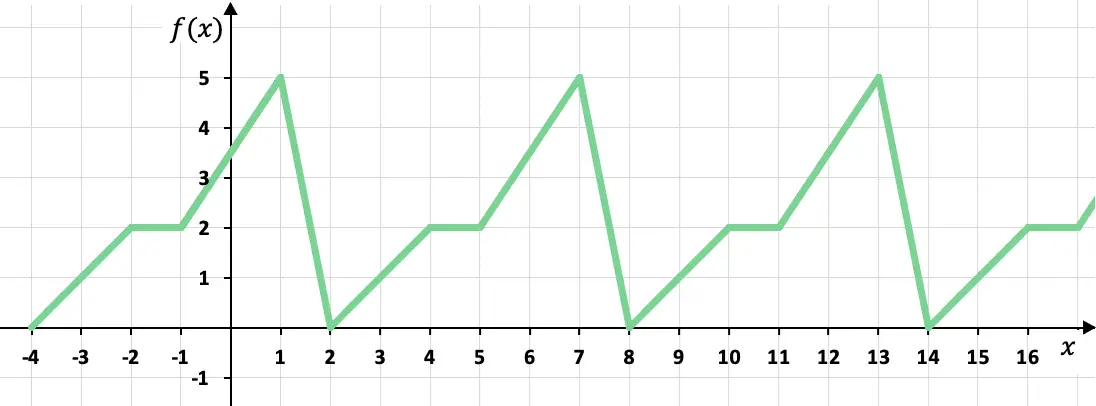
Questa funzione definita a tratti è una funzione periodica, poiché i valori del suo grafico si ripetono ciclicamente. Più precisamente la funzione assume lo stesso valore ogni sei x, quindi il periodo della funzione è pari a 6.
![]()
Esempio 2
Trova la periodicità della seguente funzione:
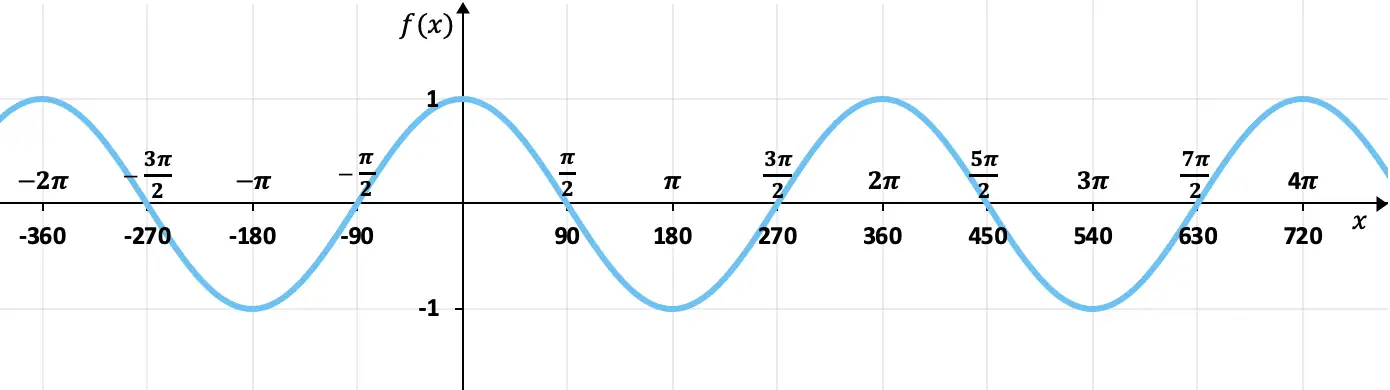
Questa funzione corrisponde alla rappresentazione grafica di una funzione trigonometrica, più precisamente della funzione coseno.
Come possiamo vedere dal grafico, la funzione ripete periodicamente i suoi valori, quindi è una funzione periodica. Inoltre, tra picco e picco dell’onda c’è uno spazio di 2π (o 360º), quindi questo è il periodo della funzione.
![]()
Periodicità delle funzioni trigonometriche
Periodicità e funzioni trigonometriche sono strettamente correlate, infatti, una delle caratteristiche principali di questo tipo di funzioni è che la maggior parte delle funzioni trigonometriche sono periodiche.
Successivamente studieremo la periodicità delle 3 principali funzioni trigonometriche: seno, coseno e tangente.
Periodo della funzione seno
L’espressione per la funzione seno è la seguente:
![]()
In questo caso non è necessario rappresentare graficamente la funzione per ricavarne il periodo, ma è possibile calcolarlo semplicemente applicando la seguente formula:
![]()
Inoltre, la funzione seno ha la particolarità che se cambiamo il suo periodo, cambiamo anche la forma del suo grafico. Puoi vedere come il valore del periodo influenza la sua rappresentazione grafica nel seguente link:
➤ Vedi: Grafico della funzione seno
Periodo della funzione coseno
L’espressione algebrica della funzione coseno è la seguente:
![]()
Come per il seno, il periodo della funzione coseno può essere trovato direttamente utilizzando la seguente formula:
![]()
Il valore del periodo coseno determina completamente il suo grafico, clicca sul seguente link e scopri il perché:
➤ Vedi: Grafico della funzione coseno
Periodo della funzione tangente
La funzione tangente è descritta matematicamente:
![]()
Il periodo della funzione tangente si calcola con la stessa formula di quello del seno e del coseno:
![]()
Tuttavia, il grafico della funzione tangente è diverso dal seno e dal coseno perché ha anche asintoti che si ripetono periodicamente. Puoi vedere questa e altre caratteristiche di questa funzione trigonometrica al seguente link:
➤ Vedi: Grafico della funzione tangente