Parabola (matematica): definizione, equazione, elementi, esempi,…

In questa pagina troverai tutto sulla parabola: cos’è, cosa rappresenta, i suoi elementi (fuoco, direttrice, vertice, ecc.) la sua equazione (con i diversi tipi di equazioni della parabola), esempi, esercizi risolti, le sue proprietà, le sue applicazioni,…

Cos’è una parabola?

La parabola è un concetto che ha significati molto diversi, ma la sua definizione matematica è la seguente:

In matematica, una parabola è il luogo dei punti del piano equidistanti da un punto fisso (chiamato fuoco) e da una linea fissa (chiamata direttrice).

Pertanto ogni punto della parabola è alla stessa distanza dal suo fuoco e dalla sua direttrice.

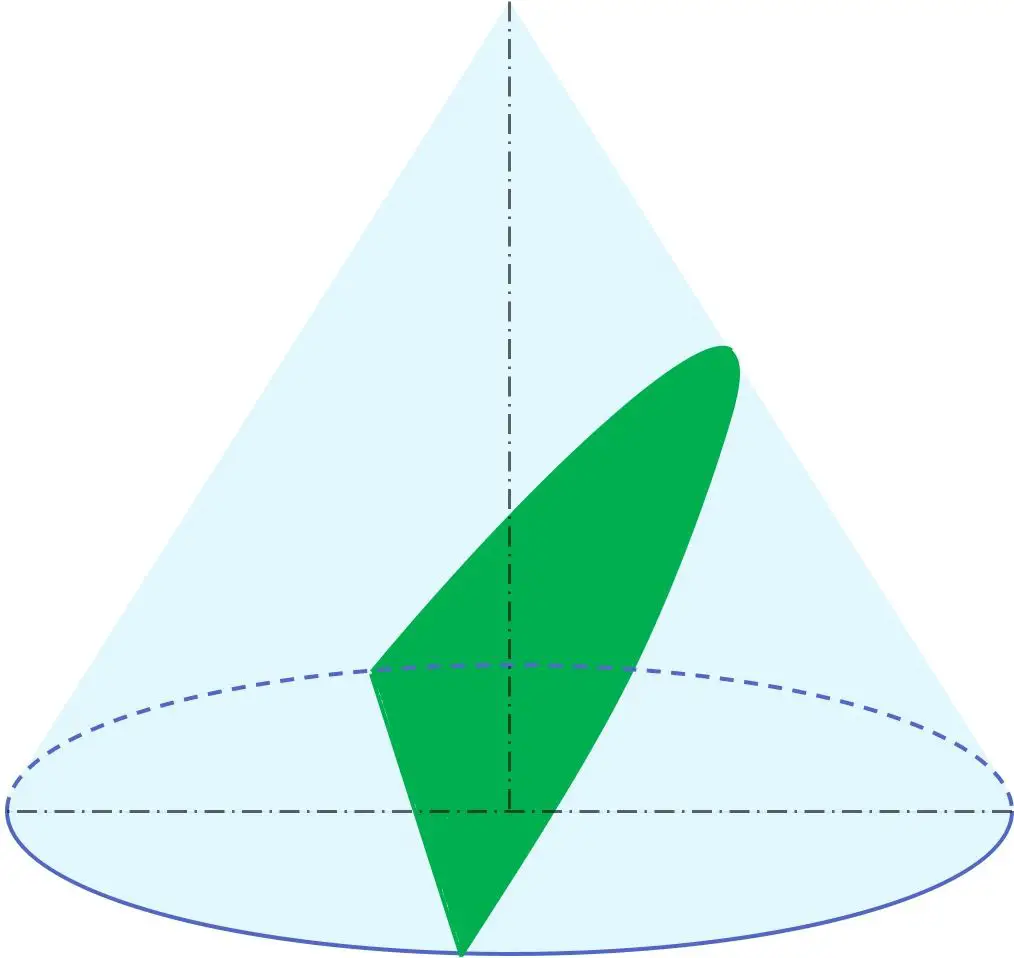
Inoltre, in geometria, la parabola è una delle sezioni coniche insieme alla circonferenza, all’ellisse e all’iperbole. In altre parole, da un cono si può ricavare una parabola.

In particolare, la parabola risulta dalla sezione di un cono mediante un piano avente un angolo di inclinazione rispetto all’asse di rivoluzione equivalente all’angolo generatore del cono. Pertanto il piano contenente la parabola è parallelo alla generatrice del cono.

Elementi di una parabola

Le caratteristiche di una parabola dipendono dai seguenti elementi:

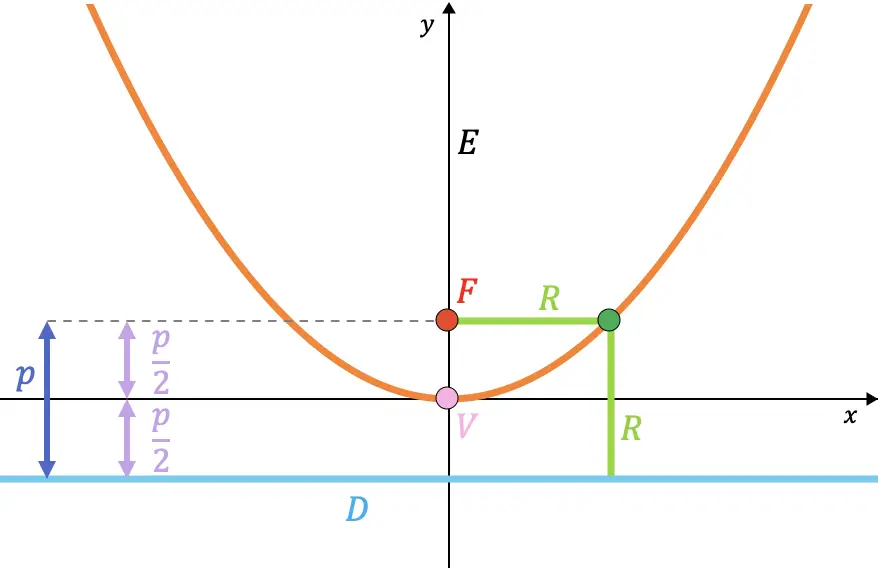
Fuoco (F) : è un punto fisso all’interno della parabola. La distanza da un punto qualsiasi della parabola al fuoco è uguale alla distanza da questo stesso punto alla direttrice della parabola.
Direttrice (D) : è una retta fissa esterna alla parabola. Un punto della parabola è alla stessa distanza dalla direttrice e dal fuoco della parabola.
Parametro (p) : è la distanza dal fuoco al regista.
Vettore raggio (R) : è il segmento che congiunge un punto della parabola al fuoco. Il suo valore coincide con la distanza dal punto alla direttrice.
Asse (E) : è la retta perpendicolare alla direttrice che passa per il fuoco ed è l’asse di simmetria della parabola, nel grafico sottostante corrisponde all’asse del computer (asse Y). Chiamato anche asse focale.
Vertice (V) : è il punto di intersezione tra la parabola e il suo asse.
Lunghezza focale : è la distanza tra il fuoco e il vertice, oppure tra la direttrice e il vertice. Il suo valore è sempre uguale a
$\displaystyle \frac{p}{2}.$

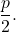
lato destro

Il lato destro di una parabola è la corda interna alla parabola che passa per il fuoco ed è parallela alla direttrice.

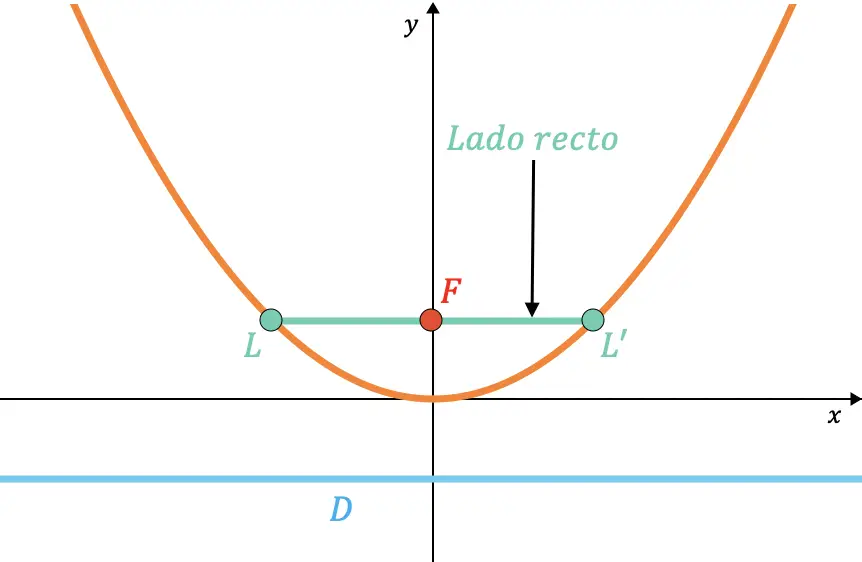
Allo stesso modo si può dimostrare che la lunghezza del lato destro è sempre il doppio del valore del parametro

$p.$

$\lvert LL'\rvert = 2p$

D’altra parte, le due rette tangenti alla parabola che passano per gli estremi del lato destro formano un angolo di 45º con il lato destro stesso e si intersecano anche al vertice della parabola.

equazioni della parabola

L’equazione di una parabola è un tipo di funzione quadratica perché deve sempre avere almeno 1 termine quadrato. Inoltre, l’equazione di una parabola dipende dal suo orientamento orizzontale o verticale.

Pertanto, nella geometria analitica, ci sono diversi modi per esprimere matematicamente una parabola: l’ equazione canonica o ridotta , l’ equazione ordinaria e l’ equazione generale della parabola.

Equazione ridotta o canonica della parabola

Ciò che differenzia l’equazione ridotta o canonica dalle altre equazioni paraboliche è che il vertice della parabola è l’origine delle coordinate , cioè il punto (0,0).

La forma dell’equazione ridotta della parabola dipende dal fatto che sia orizzontale o verticale. Osservate la seguente rappresentazione grafica dove sono indicate le 4 possibili varianti:

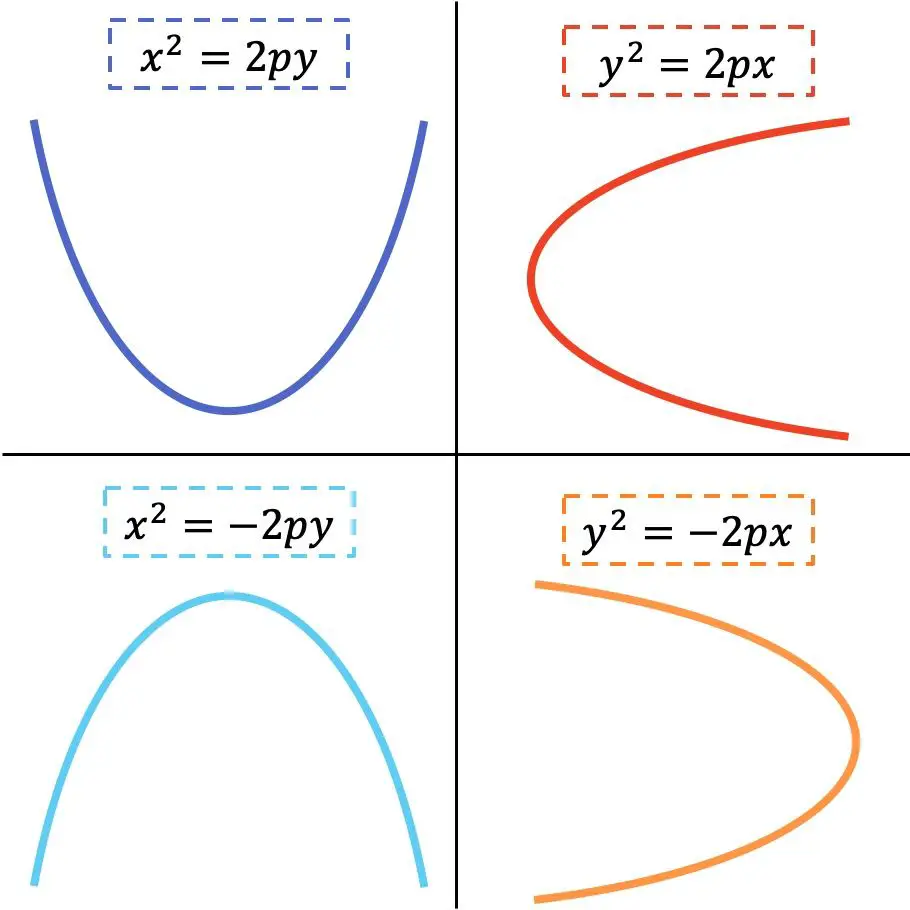
Oro

$p$

è il parametro caratteristico della parabola.

Come puoi vedere nell’immagine precedente, quando la variabile x è quadrata, la parabola è verticale, mentre quando la variabile y è quadrata, la parabola è orizzontale. D’altra parte, la direzione dei rami della parabola dipende dal segno dell’equazione.

Equazione ordinaria della parabola

Abbiamo appena visto come si presenta l’equazione della parabola quando il suo vertice o centro corrisponde all’origine delle coordinate (l’equazione ridotta o canonica), ma qual è l’equazione della parabola se il vertice è fuori dall’origine?

Quando il vertice della parabola è un punto qualsiasi, si usa l’equazione ordinaria della parabola , la cui espressione è:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}}(x-x_0 )^2 = 2p (y-y_0) \quad}$

dove il centro o vertice della parabola è il punto

$V(x_0,y_0).$

L’equazione precedente corrisponde alla parabola orientata verticalmente, cioè l’asse focale della parabola è parallelo all’asse Y.

Allo stesso modo, per definire una parabola orientata orizzontalmente (il suo asse focale è parallelo all’asse X), dobbiamo utilizzare la seguente variante dell’equazione ordinaria della parabola:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} (y-y_0 )^2 = 2p (x-x_0)\quad}$

Dove, come prima, il centro o vertice della parabola è il punto

$V(x_0,y_0).$

Equazione generale della parabola

Finora tutte le equazioni delle parabole che abbiamo analizzato vengono utilizzate per esprimere parabole orizzontali o verticali. Ma ovviamente una parabola può essere anche obliqua o inclinata .

Ebbene, per esprimere questo tipo di parabola, utilizziamo l’ equazione generale della parabola , la cui formula è la seguente:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} Ax^2 + Bxy+Cy^2 +Dx+Ey + F = 0 \quad}$

L’equazione di cui sopra è una parabola se e solo se i coefficienti

$A$

$C$

non sono contemporaneamente nulli e, inoltre, è soddisfatta la seguente condizione:

$B^2-4AC =0$

Esempio di come trovare vertice, fuoco e direttrice di una parabola dalla sua equazione

In molti esercizi e problemi sulle parabole ti viene chiesto di calcolare il vertice, il fuoco e la direttrice di una certa parabola. Vediamo quindi come si realizza attraverso un esempio:

Trova il vertice, il fuoco e la direttrice della seguente parabola:

$x^2 = 4y$

La cosa fondamentale per risolvere questo tipo di problema di parabola è determinare il parametro p della parabola . In questo caso l’equazione della parabola corrisponde all’equazione ridotta o canonica (parabola verticale):

$x^2 = 2py$

Pertanto il parametro p è:

$2p = 4$

$p = \cfrac{4}{2}$

$p = 2$

D’altra parte, poiché la parabola segue l’equazione ridotta o canonica, ciò significa che il suo vertice o centro è nell’origine delle coordinate:

$\bm{V(0,0)}$

Una volta che conosciamo il vertice e il valore del parametro della parabola, possiamo facilmente trovarne il fuoco e la direttrice.

Il termine quadratico dell’equazione è la variabile x per cui l’asse della parabola sarà parallelo all’asse OY e, infatti, poiché il suo vertice è il punto (0,0), l’asse della parabola sarà l’OY asse stesso. Quindi il fuoco di una parabola si trova sempre sull’asse della parabola e ad una distanza di

$p/2$

dal vertice della parabola, quindi le sue coordinate sono:

$\displaystyle F\left(0, \frac{p}{2} \right)$

$\displaystyle F\left(0, \frac{2}{2} \right)$

$\displaystyle \bm{F\left(0,1 \right)}$

Allo stesso modo, la linea guida sarà la linea orizzontale che si trova a distanza

$p/2$

dal vertice della parabola, che è l’origine delle coordinate. L’equazione della retta sarà quindi:

$y=-\cfrac{p}{2}$

$y=-\cfrac{2}{2}$

$\bm{y=-1}}$

La parabola è stata rappresentata graficamente di seguito in modo da poter controllare i risultati:

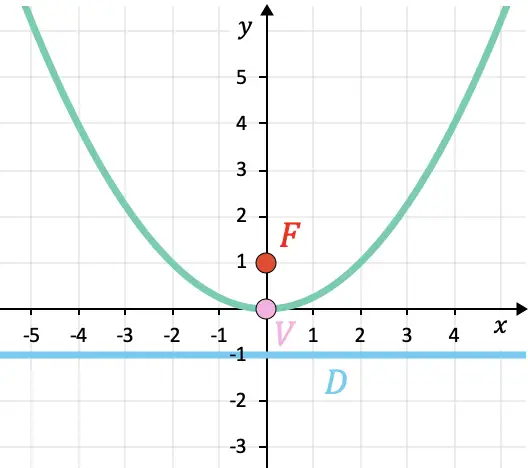
Esercizi di equazione della parabola risolti

Proprietà delle parabole

Tutte le parabole hanno le seguenti proprietà:

Una parabola è una curva aperta, ovvero è composta da due rami senza punti in comune che si estendono in modo illimitato.
Ogni parabola ha un unico asse di simmetria, dove si trova il vertice di detta parabola.
Una parabola orientata verticalmente è convessa quando i suoi rami salgono; la parabola è invece concava se i suoi rami scendono.
L’eccentricità di una parabola equivale all’unità (1). L’eccentricità è un coefficiente che in questo caso si calcola dividendo la distanza dal fuoco al centro della parabola per la distanza dal vertice alla direttrice (e le due distanze coincidono sempre nel loro valore).
Dalla proprietà precedente segue che tutte le parabole sono simili o simili.
Una parabola non ha asintoti.

applicazioni paraboliche

Ora che hai molta familiarità con il significato di una parabola, potresti chiederti… qual è lo scopo di una parabola?

Ebbene, anche se non ti sembra, la forma geometrica della parabola è molto comune nella vita reale. Ad esempio, molte volte quando si lancia una palla si fa un movimento parabolico, soprattutto nel basket. Ebbene, l’equazione della parabola è molto utile per studiare analiticamente il percorso parabolico che segue la palla.

Un’altra applicazione della parabola riguarda le antenne (da cui il nome antenna parabolica). Poiché ogni raggio che cade su un oggetto di forma parabolica parallela all’asse di simmetria viene riflesso direttamente verso il fuoco, cioè tutti i raggi che vanno all’antenna parabolica sono concentrati nel fuoco e questo può essere utilizzato in diversi modi. Ecco perché il focus di una parabola è così importante.

Risolti i problemi relativi ai piatti

Esercizio 1

Calcola il vertice, il fuoco e la direttrice della parabola la cui equazione è la seguente:

$y^2 = 8x$

vedi soluzione

Innanzitutto la parabola sarà orizzontale perché segue la seguente espressione dell’equazione ridotta o canonica della parabola:

$y^2 = 2px$

Quindi il suo parametro p è:

$2p = 8$

$p = \cfrac{8}{2}$

$p = 4$

D’altra parte, poiché la parabola segue l’equazione ridotta o canonica, ciò significa che il suo vertice o centro è nell’origine delle coordinate:

$\bm{V(0,0)}$

Una volta che conosciamo il vertice e il valore del parametro della parabola, possiamo facilmente calcolarne il fuoco e la direttrice.

Il termine quadratico dell’equazione è la variabile e cioè l’asse della parabola sarà parallelo all’asse OX e, infatti, poiché il suo vertice è il punto (0,0), l L’asse della parabola sarà l’asse OX stesso. Quindi il fuoco di una parabola si trova sempre sull’asse della parabola e ad una distanza di

$p/2$

dal vertice della parabola, le cui coordinate sono:

$\displaystyle F\left(\frac{p}{2},0\right)$

$\displaystyle F\left(\frac{4}{2},0\right)$

$\displaystyle \bm{F\left(2,0 \right)}$

Allo stesso modo, la linea guida è a distanza

$p/2$

dal vertice della parabola, che è l’origine delle coordinate ed è perpendicolare al suo asse focale. L’equazione della linea direttrice è quindi:

$x=-\cfrac{p}{2}$

$x=-\cfrac{4}{2}$

$\bm{x=-2}}$

Esercizio 2

Trovare il vertice, il fuoco e la direttrice della parabola la cui equazione è la seguente:

$(x-4)^2 = -16(y+1)$

vedi soluzione

La parabola è definita secondo la sua equazione ordinaria (asse parallelo all’asse Y), la cui formula è:

$(x-x_0 )^2 = 2p (y-y_0)$

Quindi il suo parametro p è:

$2p = -16$

$p =- \cfrac{16}{2}$

$p =- 8$

Invece in questo caso l’equazione ordinaria della parabola implica che il suo centro non sia nell’origine delle coordinate, invece le coordinate cartesiane del vertice della parabola sono i numeri tra parentesi con il segno cambiato :

$\bm{V(4,-1)}$

Una volta che conosciamo il vertice e il valore del parametro della parabola, possiamo calcolarne il fuoco e la direttrice.

Il termine quadratico dell’equazione è la variabile x tale che l’asse della parabola è parallelo all’asse OY. Pertanto, il fuoco di una parabola si trova sempre sull’asse della parabola e ad una distanza di

$p/2$

dal vertice della parabola, in modo che le coordinate del punto focale siano quelle del vertice sommando

$p/2$

verticalmente:

$\displaystyle F\left(4,-1+\frac{p}{2}\right)$

$\displaystyle F\left(4,-1+\frac{-8}{2}\right)$

$\displaystyle F\left(4,-1-4\right)$

$\displaystyle \bm{F\left(4,-5 \right)}$

Allo stesso modo, la direttrice sarà la linea orizzontale situata a distanza

$p/2$

dal vertice della parabola. L’equazione della linea direttrice è quindi:

$y=-1-\cfrac{-p}{2}$

$y=-1-\cfrac{-8}{2}$

$y=-1+4$

$\bm{y=3}}$

Esercizio 3

Determina l’equazione parabolica il cui asse è parallelo all’asse delle ascisse, ha come vertice il punto V(5,2) e il suo fuoco è il punto P(8,2).

vedi soluzione

In questo caso il vertice della parabola non è l’origine delle coordinate, quindi abbiamo bisogno dell’equazione ordinaria per definire la parabola dell’enunciato. Inoltre, l’asse focale della parabola è parallelo all’asse x, il che significa che la parabola sarà orientata orizzontalmente (i rami andranno a destra o a sinistra) e quindi il termine quadratico dell’equazione dovrà essere la variabile y :

$(y-y_0 )^2 = 2p (x-x_0)$