Operazioni con i monomi

Settembre 17, 2023

In questa pagina spieghiamo come eseguire tutte le operazioni con i monomi (addizione, sottrazione, moltiplicazione, divisione e potenza). Inoltre, potrai vedere esempi di ogni tipo di operazione con monomi ed esercitarti con esercizi risolti passo dopo passo.

Addizione e sottrazione di monomi

Due o più monomi possono essere sommati o sottratti solo se sono monomi simili, cioè se i due monomi hanno una parte letterale identica (stesse lettere e stessi esponenti).

Allora la somma (o sottrazione) di due monomi simili è uguale ad un altro monomio composto dalla stessa parte letterale e dalla somma (o sottrazione) dei coefficienti di questi due monomi.

L’addizione e la sottrazione di monomi sono anche chiamate rispettivamente addizione e sottrazione di monomi.

Esempi di addizione e sottrazione di monomi

Affinché tu possa capire chiaramente come sommare e sottrarre due o più monomi, ti lasciamo diversi esempi di seguito:

$4x^6+3x^6 = 7x^6$
$5y^3-2y^3 = 3y^3$
$2x^2y+5x^2y-3x^2y = 4x^2y$
$6abc-7abc+4abc = 3abc$
$6x^3y^2-4x^3y+2x^2y^3 = \color{red} \bm{\times}$

I monomi dell’ultimo esempio non possono essere sommati né sottratti perché non sono simili o, in altre parole, hanno incognite o esponenti diversi.

Prodotto di un numero di volte monomiale

Per risolvere il prodotto di un monomio per un numero, moltiplica semplicemente il coefficiente del monomio per quel numero, lasciando invariata la parte letterale del monomio.

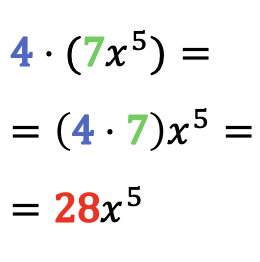
Esempi di moltiplicazione di numeri per monomi

$2\cdot (6x^3) = (2\cdot 6)x^3 = 12x^3$
$-4\cdot (5x^7) = (-4\cdot 5)x^7 = -20x^7$
$5\cdot (-3a^4b) = (5\cdot (-3))a^4b = -15a^4b$
$-7(-6x^9y^5)= (-7\cdot (-6))x^9y^5=42x^9y^5$

Moltiplicazione di monomi

Il risultato della moltiplicazione di due monomi è un altro monomio il cui coefficiente è il prodotto dei coefficienti dei monomi e la cui parte letterale si ottiene moltiplicando le variabili che hanno la stessa base, cioè sommando i loro esponenti.

Pertanto, per moltiplicare due monomi diversi, dobbiamo moltiplicare i coefficienti tra loro e sommare gli esponenti delle potenze che hanno la stessa base.

Tuttavia, se moltiplichiamo due monomi con potenze di base diverse , dobbiamo semplicemente moltiplicare insieme i loro coefficienti e lasciare le stesse potenze. Per esempio:

$5x^2\cdot 3y^4 = (5\cdot 3) x^2y^4 = 15x^2y^4$

D’altra parte, quando si moltiplicano i monomi, è necessario tenere conto della regola dei segni:

Un monomio positivo moltiplicato per un monomio positivo dà un altro monomio positivo.
Un monomio positivo moltiplicato per un monomio negativo (o viceversa) equivale a un monomio negativo.
Due monomi negativi moltiplicati insieme danno origine a un monomio positivo.

Esempi di moltiplicazioni monomiali

Di seguito sono riportati alcuni esempi di moltiplicazione tra monomi in modo da poter vedere come è fatto:

$6x^4 \cdot 7x^5= (6\cdot 7)x^{4+5} = 42x^9$
$4y \cdot 2y^3 = (4\cdot 2)y^{1+3} = 8 y^4$
$5x^2y^4\cdot (-8x^8y^2)=(5\cdot (-8))x^{2+8}y^{4+2} = -40x^{10}y^6$
$-3x^6y^4 \cdot (-4x^2z)= (-3\cdot (-4)) x^{6+2}y^4z= 12x^8y^4z$
$-3x^8\cdot 4x^5\cdot (-x^2) =-12x^{13}\cdot (-x^2)= 12x^{15}$

Come hai visto, risolvere una moltiplicazione di monomi è relativamente semplice. Ma dovresti tenere presente che i monomi possono anche essere moltiplicati per polinomi, e anche 2 o più polinomi possono essere moltiplicati insieme. Se sei più interessato, puoi vedere come funzionano tutte queste operazioni cliccando su Moltiplicazione polinomiale .

Divisione dei monomi

In matematica, il risultato della divisione dei monomi è un altro monomio il cui coefficiente è equivalente al quoziente dei coefficienti dei monomi e la cui parte letterale si ottiene dividendo le variabili che hanno la stessa base, cioè sottraendo i loro esponenti .

Ovviamente qualsiasi divisione di monomi può essere espressa anche come frazione:

$8x^3y^2z : 2x^2y = \cfrac{8x^3y^2z}{2x^2y} = 4xyz$

Come nella moltiplicazione, nella divisione dei monomi è necessario applicare la legge dei segni:

Un monomio positivo diviso per un monomio positivo dà un altro monomio positivo.
Un monomio positivo diviso per un monomio negativo (o viceversa) equivale a un monomio negativo.
Due monomi negativi divisi tra loro danno origine a un monomio positivo.

Esempi di divisione di monomi

Di seguito puoi vedere altri esempi di come vengono divisi due o più monomi:

$7x^6 : 7x^4= (7:7)x^{6-4} = 1x^2=x^2$
$12y^5 : 4y^2= (12:4)y^{5-2} = 3y^3$
$15x^7y^6 :3x^4y^5= (15:3)x^{7-4}y^{6-5} = 5x^3y$
$27x^9y^7 :(-3x^5y^2)= (27:(-3))x^{9-5}y^{7-2}= -9x^4y^5$
$-18x^{13} : 3x^4 : (-2x^7) = -6x^9: (-2x^7) = 3x^2$

Sicuramente ad un certo punto, quando hai imparato qualcosa di nuovo in matematica, ti sei chiesto: a cosa serve ? Ebbene, la divisione monomiale viene utilizzata per dividere i polinomi. In effetti, è abbastanza comune commettere un errore dividendo i polinomi perché due monomi sono stati divisi in modo errato. Per questo motivo ti consigliamo, ora che hai familiarità con la divisione tra monomi, di vedere come si calcola la divisione tra polinomi , perché ora ti sarà molto più semplice imparare la procedura (è piuttosto complicata).

Potenza di un monomio

In matematica, per calcolare la potenza di un monomio, ogni elemento del monomio viene elevato all’esponente della potenza . In altre parole, la potenza di un monomio consiste nell’elevare il suo coefficiente e le sue variabili (lettere) all’esponente della potenza.

come si risolvono le operazioni con i monomi

Ricorda dalle proprietà delle potenze che quando entrambi elevano un termine già elevato, gli esponenti si moltiplicano. Ecco perché , alla potenza di un monomio, l’esponente di ciascuna lettera va sempre moltiplicato per l’esponente che indica la potenza .

D’altra parte, per effettuare correttamente questa operazione è necessario ricordare la seguente proprietà dei poteri:

Un monomio negativo elevato ad esponente pari equivale a un monomio positivo.
Invece, un monomio negativo elevato a un esponente dispari risulta in un monomio negativo.

Esempi di potenze di monomi

Vi lasciamo con alcuni esempi affinché possiate comprendere chiaramente come si calcola la potenza di un monomio:

$\left(5x^6\right)^2 = 5^2\left(x^6\right)^2 = 5^2x^{6\cdot 2} = 25x^{12}$
$\left(2x^5\right)^4 = 2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = 16x^{20}$
$\left(-4y^3\right)^2 = (-4)^2\left(y^3\right)^2 = (-4)^2y^{3\cdot 2} = 16y^{6}$
$\left(3x^4y\right)^3 = 3^3\left(x^4y\right)^3 = 3^3x^{4\cdot 3}y^{1\cdot 3} = 27x^{12}y^3$
$\left(-2a^5b^7\right)^3 = (-2)^3\left(a^5b^7\right)^3 = (-2)^3a^{5\cdot 3}b^{7\cdot 3} = -8a^{15}b^{21}$

Operazioni combinate con monomi

Una volta che hai visto quali sono tutte le operazioni con i monomi, sappi che possono anche essere combinate tra loro. Possiamo cioè trovare esercizi in cui ci viene chiesto di risolvere operazioni con monomi in cui sono coinvolte tutte le tipologie: addizione, sottrazione, moltiplicazione, divisione e potenze.

Ma non preoccuparti, non sono così difficili come sembrano. L’unica cosa che devi ricordare è l’ordine in cui vengono risolte le operazioni combinate:

Innanzitutto vengono risolte le operazioni con i monomi tra parentesi.
Successivamente si calcolano le potenze dei monomi.
In terzo luogo, vengono eseguite moltiplicazioni e divisioni dei monomi.
Infine, vengono determinate le addizioni e le sottrazioni dei monomi.

Sono sicuro che risolvendo un esempio lo vedrai più chiaramente:

Esempio di operazione combinata di monomi

$12x^9:(2x^4-8x^4)+3x^4\cdot 6x - (x^3\cdot 7x^2)$

Innanzitutto dobbiamo risolvere le operazioni con i monomi tra parentesi:

$12x^9:(-6x^4)+3x^4\cdot 6x - 7x^5$

In questo caso non abbiamo alcun potere. Quindi ora calcoliamo le moltiplicazioni e le divisioni dei monomi:

$-2x^5+18x^5 - 7x^5$

E infine, aggiungiamo e sottraiamo i monomi:

$16x^5 - 7x^5$

$\bm{9x^5}$

Esercizi risolti su operazioni con monomi

Nel caso in cui vogliate esercitarvi, vi lasciamo di seguito diversi esercizi risolti passo passo di difficoltà ESO su operazioni con monomi.

Esercizio 1

Calcolare le seguenti addizioni e sottrazioni di monomi:

$\text{A)} \ 2x^4+9x^4$

$\text{B)} \ -3x^5y^3 +4x^5y^3$

$\text{C)} \ 3x^8-6x^8+2x^8$

$\text{D)} \ -2a^3b^2-5a^3b^2+3a^3b^2-7a^3b^2+4a^3b^2$

$\text{E)} \ 6xyz-5xz-7xyz-8xz$

$\text{F)} \ 6y^3+2y^3-y^5+8y^4-y^5-5y^3$

Vedi la soluzione

$\text{A)} \ 2x^4+9x^4= \bm{11x^4}$

$\text{B)} \ -3x^5y^3 +4x^5y^3= \bm{x^5y^3}$

$\text{C)} \ 3x^8-6x^8+2x^8= \bm{-x^8}$

$\text{D)} \ -2a^3b^2-5a^3b^2+3a^3b^2-7a^3b^2+4a^3b^2=\bm{-7a^3b^2}$

$\text{E)} \ 6xyz-5xz-7xyz-8xz= \bm{-xyz-13xz}$

$\text{F)} \ 6y^3+2y^3-y^5+8y^4-y^5-5y^3 = \bm{-2y^5+8y^4+3y^3}$

Esercizio 2

Risolvi le seguenti moltiplicazioni di monomi:

$\text{A)} \ 5x^7\cdot 6x^2$

$\text{B)} \ 2y^8\cdot (-5y^6)$

$\text{C)} \ -4a^3 \cdot (-2a)$

$\text{D)} \ 2x^3\cdot 4x \cdot (-3x^6)$

$\text{E)} \ -5x^6\cdot (-x^3) \cdot (-9x^4)$

$\text{F)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)$

Vedi la soluzione

$\text{A)} \ 5x^7\cdot 6x^2=(5\cdot 6)x^{7+2} = \bm{30x^9}$

$\text{B)} \ 2y^8\cdot (-5y^6)= (2\cdot (-5))y^{8+6} = \bm{-10y^{14}}$

$\text{C)} \ -4a^3 \cdot (-2a) =(-4\cdot (-2))a^{3+1} = \bm{8a^4}$

$\text{D)} \ 2x^3\cdot 4x \cdot (-3x^6) = 8x^4\cdot (-3x^6) = \bm{-24x^{10}}$

$\text{E)} \ -5x^6\cdot (-x^3) \cdot (-9x^4)=5x^9\cdot (-9x^4) =\bm{-45x^{13}}$

$\text{F)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)= <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-bb20ebb96e0dff759d07813f6fff9470_l3.png" height="22" width="195" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[35x^{11}y^2z^4\cdot (-2x^2y^5z^3) =\]" title="Rendered by QuickLaTeX.com"/> \bm{-70x^{13}y^7z^7}” title=”Rendered by QuickLaTeX.com”> <div class=$

Esercizio 3

Determinare il risultato delle seguenti divisioni di monomi:

$\text{A)} \ 24x^4: 6x^2$

$\text{B)} \ 16a^9: (-2a^6)$

$\text{C)} \ -21x^3:(-3x)$

$\text{D)} \ 14x^8y^3 :2x^6y$

$\text{E)} \ 42x^5y^3z^6 : 7x^2y^3z^4$

$\text{F)} \ 48x^8y^6z^{10} : (-6x^4y^{2}z^4) : (-4x^2y^2z^3)$

Vedi la soluzione

$\text{A)} \ 24x^4: 6x^2 = (24:6)x^{4-2} = \bm{4x^2}$

$\text{B)} \ 16a^9: (-2a^6)= (16:(-2))a^{9-6} = \bm{-8a^3}$

$\text{C)} \ -21x^3:(-3x) = (-21:(-3))x^{3-1} = \bm{7x^2}$

$\text{D)} \ 14x^8y^3 :2x^6y = \bm{7x^2y^2}$

$\text{E)} \ 42x^5y^3z^6 : 7x^2y^3z^4= 6x^3y^0z^2=\bm{6x^3z^2}$

Nell’operazione precedente abbiamo semplificato il termine

$y^0$

perché qualsiasi numero elevato a 0 è uguale a 1. Quindi:

$6x^3y^0z^2=6x^3\cdot 1 \cdot z^2=\bm{6x^3z^2}$

$\text{F)} \ 48x^8y^6z^{10} : (-6x^4y^{2}z^4) : (-4x^2y^2z^3)= <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-6dc0e068dbf84cef6abfe7e1789d245b_l3.png" height="22" width="194" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[-8x^4y^4z^6: (-4x^2y^2z^3)=\]" title="Rendered by QuickLaTeX.com"/> \bm{2x^2y^2z^3}” title=”Rendered by QuickLaTeX.com”> <div class=$

Esercizio 4

Trova le seguenti potenze dei monomi:

$\text{A)} \ \left(-8x^4\right)^2$

$\text{B)} \ \left(-2a^7\right)^3$

$\text{C)} \ \left(5x^8y^2\right)^3$

$\text{D)} \ \left(-x^3y^5z\right)^6$

$\text{E)} \ \left(-2x^5y^4\right)^5$

Vedi la soluzione

$\text{A)} \ \left(-8x^4\right)^2=(-8)^2\left(x^4\right)^2 = (-8)^2x^{4\cdot 2} = \bm{64x^{8}}$

$\text{B)} \ \left(-2a^7\right)^3=(-2)^3\left(a^7\right)^3 = (-2)^3a^{7\cdot 3} = \bm{-8a^{21}}$

$\text{C)} \ \left(5x^8y^2\right)^3=(5)^3\left(x^8y^2\right)^3 = \bm{125x^{24}y^6}$

$\text{D)} \ \left(-x^3y^5z\right)^6=(-1)^6\left(x^3y^5z\right)^6 = \bm{x^{18}y^{30}z^{6}}$

$\text{E)} \ \left(-2x^5y^4\right)^5 =(-2)^5\left(x^5y^4\right)^5 = \bm{-32x^{25}y^{20}}$

Esercizio 5

Risolvi le seguenti operazioni combinate con i monomi e semplifica il più possibile:

$\text{A)} \ 3x^2\cdot 4x^5 : 2x^4 + 10x^6:(-2x^4)\cdot 6x$

$\text{B)} \ 4\cdot \left(5x^4 -2x^4\right)^2$

$\text{C)} \ 8x^7:(-4x^3+3x^3-7x^3)-5x^3\cdot 3x$

$\text{D)} \ \left(-2x^2y\right)^3+4x^2 \cdot 5\left(xy\right)^4:(-2y)$

$\text{E)} \ 8x^8:\left(-2x^3\right)^2-(7x^3\cdot 6x^6): (-2x^4)$

Vedi la soluzione

$\color{blue} \mathbf{A}\bm{)} \color{black} \ 3x^2\cdot 4x^5 : 2x^4 + 10x^6:(-2x^4)\cdot 6x$

$12x^7 : 2x^4 -5x^2\cdot 6x$

$6x^3 -30x^3$

$\bm{-24x^3}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ 4\cdot \left(5x^4 -2x^4\right)^2$

$4\cdot \left(3x^4 \right)^2$

$4\cdot 9x^8$

$\bm{36x^8}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ 8x^7:(-4x^3+3x^3-7x^3)-5x^3\cdot 3x$

$8x^7:(-8x^3)-5x^3\cdot 3x$

$-x^4-15x^4$

$\bm{-16x^4}$

$\color{blue} \mathbf{D}\bm{)} \color{black} \ \left(-2x^2y\right)^3+4x^2 \cdot 5\left(xy\right)^4:(-2y)$

$-8x^6y^3+4x^2 \cdot 5\cdot x^4y^4:(-2y)$

$-8x^6y^3+4x^2 \cdot 5x^4y^4:(-2y)$

$-8x^6y^3+20x^6y^4:(-2y)$

$-8x^6y^3-10x^6y^3$

$\bm{-18x^6y^3}$

$\color{blue} \mathbf{E}\bm{)} \color{black} \ 8x^8:\left(-2x^3\right)^2-(7x^3\cdot 6x^6): (-2x^4)$

$8x^8:\left(-2x^3\right)^2-42x^9: (-2x^4)$

$8x^8:4x^6-42x^9: (-2x^4)$

$\bm{2x^2+21x^5}$

L’operazione non può essere ulteriormente semplificata perché i due monomi hanno esponenti diversi, quindi il risultato è un polinomio.

Se sei arrivato fin qui, significa che hai già padroneggiato tutte le operazioni con i monomi. Luminoso! Bene, un’altra operazione che sicuramente ti interesserà è il fattoriale di un numero. Si tratta di un’operazione piuttosto curiosa, poiché viene calcolata diversamente dalle altre. E, in effetti, molte persone non sanno quale sia il fattoriale di un numero. Scopri come risolvere un fattoriale cliccando su questo link.

Addizione e sottrazione di monomi

Esempi di addizione e sottrazione di monomi

Prodotto di un numero di volte monomiale

Esempi di moltiplicazione di numeri per monomi

Moltiplicazione di monomi

Esempi di moltiplicazioni monomiali

Divisione dei monomi

Esempi di divisione di monomi

Potenza di un monomio

Esempi di potenze di monomi

Operazioni combinate con monomi

Esempio di operazione combinata di monomi

Esercizi risolti su operazioni con monomi

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Lascia un commento Annulla risposta