In questo articolo spieghiamo quali operazioni si possono eseguire con le funzioni. Potrai vedere la spiegazione e gli esercizi risolti sulle operazioni con funzioni. E infine troverai le proprietà delle operazioni con le funzioni.
Cosa sono le operazioni con funzioni?
Puoi eseguire 5 diversi tipi di operazioni con funzioni: addizione, sottrazione, prodotto, divisione e composizione. Cioè due funzioni possono essere sommate, sottratte, moltiplicate, divise o composte.
Successivamente vedremo come viene eseguita ogni tipologia di operazione con le funzioni e le caratteristiche di ciascuna di esse.
Somma di funzioni
Il valore della somma (o aggiunta) di due funzioni è uguale alla somma del valore di ciascuna funzione. In altre parole, per calcolare l’immagine di una funzione somma è sufficiente sommare le immagini delle funzioni coinvolte nell’operazione.
![]()
Inoltre, il dominio della somma di due funzioni è l’intersezione del dominio di ciascuna funzione sommata.
![]()
Vediamo come vengono aggiunte due funzioni utilizzando un esempio:
![]()
Aggiungiamo prima le due funzioni:
![]()
E ora troviamo il dominio della funzione somma. Per fare ciò, calcoliamo separatamente il dominio di ciascuna funzione:
![]()
➤ Vedi: come calcolare il dominio di una funzione
Quindi il dominio della funzione risultante dall’operazione sarà:
![]()
Ogni operazione con funzioni deve essere accompagnata dal suo dominio per definire completamente il risultato.
Sottrazione di funzioni
L’immagine della sottrazione (o differenza) di due funzioni è la sottrazione delle immagini di ciascuna funzione partecipante all’operazione:
![]()
Come per la funzione di addizione, il dominio di sottrazione di due funzioni equivale all’intersezione del dominio di ciascuna funzione.
![]()
Quindi, se una funzione non è definita per un certo valore della variabile indipendente x, non sarà definita neanche la funzione risultante dalla sottrazione.
Vediamo come si sottraggono due funzioni attraverso un esempio:
![]()
Per prima cosa sottraiamo le due funzioni:
![]()
E poi determiniamo il dominio della funzione di sottrazione:
![]()
![]()
Prodotto di punta
Per calcolare il prodotto o (la moltiplicazione) di due funzioni , devi semplicemente moltiplicare le espressioni di ciascuna funzione.
![]()
D’altra parte, il dominio della funzione prodotto è l’insieme delle intersezioni del dominio di ciascuna funzione moltiplicata.
![]()
Ad esempio, se abbiamo le seguenti due funzioni:
![]()
Per prima cosa eseguiamo il funzionamento del prodotto con le due funzioni:
![]()
E infine troviamo il dominio della funzione risultante dall’operazione:
![]()
![]()
Distribuzione delle funzioni
Il risultato numerico di una divisione (o quoziente) di due funzioni corrisponde alla seguente equazione:
![]()
Tuttavia il dominio di divisione di due funzioni è l’insieme delle intersezioni del dominio di ciascuna funzione meno tutte le x che annulla la funzione che funge da divisore, perché altrimenti otterremmo un’indeterminazione.
![]()
Ad esempio, divideremo le seguenti funzioni:
![]()
La distribuzione delle funzioni è la seguente:
![]()
D’altra parte, il dominio di ciascuna funzione separatamente è costituito da tutti i numeri reali
![]()
Tuttavia, poiché non può esserci uno zero al denominatore di una frazione, nel dominio della funzione risultante dobbiamo rimuovere tutti i valori che annullano il denominatore (x=3).
![]()
Composizione delle funzioni
La composizione delle funzioni è l’operazione più difficile da risolvere, perché è il concetto più complicato.
La composizione della funzione consiste nell’applicazione successiva di due funzioni. Algebricamente, la composizione di due funzioni è espressa come segue:
![]()
D’altra parte, il dominio della composizione delle funzioni
![]()
è equivalente all’insieme di tutti i valori di x nel dominio della funzione
![]()
ad esempio
![]()
appartiene al dominio della funzione
![]()
![]()
Ad esempio, date le seguenti due funzioni:
![]()
Trovare la funzione composta
![]()
seguito da
![]()
dobbiamo sostituire l’espressione di
![]()
dove ce n’è uno
![]()
nell’espressione di
![]()
![Rendered by QuickLaTeX.com \begin{aligned}(g\circ f)(x)&=g\Bigl(f(x)\Bigr)\\[2ex]&= g\Bigl(x^2+1\Bigr)\\[2ex]&=3(x^2+1)-4\\[2ex]&=3x^2+3-4\\[2ex]&=3x^2-1\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f48079d61cf80409fdbf6610b5724189_l3.png)
In questo caso, il dominio di entrambe le funzioni è costituito interamente da numeri reali, quindi anche il dominio della funzione composta sarà costituito da numeri reali.
![]()
Come puoi vedere, comporre funzioni non è un’operazione semplice da comprendere. Pertanto, ti consigliamo di esercitarti con i seguenti esercizi di composizione di funzioni:
➤ Vedi: esercizi risolti sulla composizione delle funzioni
Proprietà delle operazioni con funzioni
Di tutte le operazioni con funzioni, la somma e il prodotto sono caratterizzati dalle seguenti proprietà:
- Proprietà associativa : l’ordine in cui 3 o più funzioni vengono aggiunte o moltiplicate è irrilevante.
![]()
![]()
- Proprietà commutativa : l’ordine di addizione o moltiplicazione di due funzioni non modifica il risultato.
![]()
![]()
- Elemento neutro: l’operazione di somma e l’operazione di prodotto hanno funzioni di elemento neutro costanti
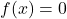
E
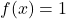
rispettivamente.
- Elemento simmetrico : la funzione somma ha la funzione opposta
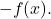
- Proprietà distributiva : questa proprietà collega la somma e il prodotto delle operazioni e si basa sulla seguente uguaglianza:
![]()