Ti sei mai chiesto in cosa differiscono i numeri razionali dagli altri numeri? In questo articolo esploreremo in modo approfondito i numeri razionali, comprese le loro caratteristiche uniche e la loro classificazione. Preparatevi a comprendere meglio il concetto!
Cosa sono i numeri razionali?
I numeri razionali (ℚ) sono una sottoclasse dei numeri reali che comprende tutti i numeri che possono essere espressi come frazioni. Ciò significa che i numeri razionali sono quelli che possono essere scritti come rapporto tra due numeri interi, a/b, dove b ≠ 0.
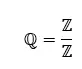
I numeri razionali possono anche essere espressi come numeri decimali ripetuti o finiti , perché sono costituiti da una serie di cifre ripetute. Alcuni esempi di numeri razionali sono 1/2, 3/4, 10/3, 2/3 e π (pi).
Sottoinsiemi di razionali
I numeri razionali possono essere divisi in due sottoinsiemi :
- Interi , che includono 0, tutti i numeri naturali e tutti i numeri negativi.
- Numeri decimali o numeri frazionari , che sono tutti quelli che esprimono valori formati da: una parte intera e una parte decimale, quest’ultima permette di esprimere valori inferiori all’unità.

Un’altra sottocategoria dell’insieme dei reali sono i numeri irrazionali , che sono un po’ più complessi.
Esempi di numeri razionali
I numeri razionali sono quelli che possono essere espressi come frazione, cioè come quoziente di due numeri interi. Ecco alcuni esempi di numeri razionali:
-23
-4/5
-1/2
-7/9
Tutte le frazioni che rappresentano un numero intero sono ugualmente razionali. Per esempio:
-1/1
-2/2
-3/3
Proprietà dei numeri razionali
La caratteristica principale dei numeri razionali è che hanno sempre un denominatore diverso da zero .
La seconda proprietà di questo insieme è che ogni numero razionale può essere rappresentato da un’infinità di frazioni equivalenti . Ad esempio, il numero razionale 3,5, che è uguale a 7/2, può essere scritto anche 14/4, 28/8… e un’infinità di altre frazioni.
I numeri razionali soddisfano anche la proprietà distributiva . Ciò significa che moltiplicare o dividere una frazione per un’altra non influirà sul risultato:
(a/b) (c/d) = (ac)/(bd)
(a/b)/(c/d) = (ad)/(bc)
Rappresentazione dei numeri razionali
I numeri razionali possono essere rappresentati in diversi modi, ma il più comune è come frazione . Una frazione è composta da due numeri: il numeratore e il denominatore.
Il numeratore indica quante parti dell’intero si considerano, mentre il denominatore indica quante parti uguali ci sono nell’intero. Ad esempio, se una torta viene divisa in otto fette uguali e se ne mangiano tre, la frazione che rappresenta la quantità di torta mangiata sarà 3/8.
Un altro modo per rappresentare i numeri razionali è tramite i decimali . I decimali sono un modo abbreviato di scrivere una frazione in cui il denominatore è un numero 10, 100, 1000, ecc. Ad esempio, se hai 1/4 di torta, questo può essere espresso come 0,25 (che significa “0 interi e 25/100”).
Tuttavia, se vogliamo rappresentarli graficamente, possiamo anche scriverli sulla linea dei numeri , dove si vede molto bene l’ordine dei numeri. Successivamente, ti mostriamo un esempio di questa riga :
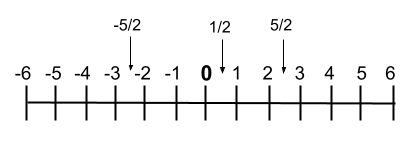
operazioni razionali
Le operazioni fondamentali dei numeri razionali sono le stesse degli interi: addizione, sottrazione, moltiplicazione e divisione. Se vuoi imparare a risolvere questo tipo di operazioni ti consigliamo di leggere il nostro articolo sulle operazioni con le frazioni .
Se però lavori con numeri razionali con base decimale, devi seguire la procedura per risolvere le operazioni che usi quando hai a che fare con i valori decimali .
Conclusione sull’insieme dei numeri razionali
Dopo questa esauriente spiegazione, possiamo concludere che l’insieme dei numeri razionali è uno dei più importanti della matematica. Contiene tutti i numeri che possono essere rappresentati come frazioni, il che ci permette di esprimere le quantità in modo molto preciso.