Fin dall’antichità l’ insieme dei numeri naturali ha costituito il fondamento su cui sono state costruite molte branche della matematica. Ad esempio, l’aritmetica e la geometria si basano su questi numeri. Ecco perché in questo breve articolo vedremo la definizione di numeri naturali e tutti i concetti legati a questo insieme.
Quali sono i numeri naturali?
I numeri naturali sono un insieme di elementi astratti che usiamo per contare e ordinare gli oggetti nel mondo fisico. In matematica l’insieme dei numeri naturali è generalmente rappresentato dalla lettera ℕ. Questo è composto da tutti i numeri interi positivi senza decimali e che non sono frazionari: ℕ = {1, 2, 3, 4, 5, 6…}.
In altre parole, i numeri naturali sono tutti quegli interi positivi che possono essere utilizzati per contare oggetti reali. In questo modo possiamo dire che il numero 1 è un numero naturale perché possiamo usarlo per contare oggetti reali. Ad esempio, possiamo avere una mela e due pere, per un totale di 3 frutti.
Nell’immagine seguente, ti mostreremo un diagramma che riassume tutti gli insiemi di numeri, così puoi vedere dove si trova l’insieme ℕ. E che rapporto ha rispetto agli altri, per assimilare meglio la nozione di numero naturale. Ti consigliamo, prima di proseguire con la spiegazione, di guardare bene la mappa concettuale e cercare di capirla.

Come fai a sapere se un numero è naturale o no?
Come abbiamo già detto, i numeri naturali sono quelli che usiamo per contare e ordinare. Per sapere se un valore è naturale o meno, dobbiamo tenere presente quanto segue : un numero ℕ non ha segno negativo, non ha cifre decimali, non ha un’unità immaginaria e non è una frazione. Successivamente, ti mostriamo un elenco dei primi 100 numeri naturali:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 6 4, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75 , 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99 e 100 .
Come si leggono e si scrivono i numeri naturali?
I numeri naturali seguono il sistema di numerazione decimale , ciò significa che i valori hanno come base aritmetica il numero dieci. Tutti i numeri sono composti da almeno una di queste nove cifre: 1, 2, 3, 4, 5, 6, 7, 8 e 9. E ricorda, in nessun caso un numero naturale ha un punto decimale o un segno negativo .
Per quanto riguarda tutte le operazioni aritmetiche questi numeri vengono scritti seguendo la notazione matematica . Se hai dubbi su un simbolo o un’espressione , ti consigliamo di accedere a quest’ultimo link e leggere l’articolo. Lì troverai tutte le informazioni relative al linguaggio matematico e tutte le notazioni.
Caratteristiche dei numeri naturali
Alcune delle caratteristiche più importanti dei numeri naturali sono:
- Il primo numero naturale è 1, poiché 0 non è un numero naturale.
- Servono per misurare, controllare e calcolare: possono essere utilizzati per misurare lunghezze, pesi, capacità, ecc.
- Possono essere confrontati tra loro: possiamo dire quale è maggiore o minore di un altro numero naturale.
- Hanno un ordine: i numeri naturali seguono un ordine logico, iniziando da 1 e terminando all’infinito.
- Due naturali non possono avere lo stesso successore, né lo stesso predecessore.
- Tutti i numeri naturali sono numeri interi, poiché i numeri naturali sono numeri interi positivi, non decimali o frazioni.
Per concludere questa sezione vi lasciamo con una serie di precisazioni su questo insieme che spesso sollevano dubbi tra gli studenti: il numero zero non è un numero naturale, i numeri naturali sono interi, i numeri naturali non possono essere numeri negativi , i numeri naturali non hanno decimali luoghi e i numeri naturali sono infiniti.
Rappresentazione dei numeri naturali
L’ insieme dei numeri naturali , detto anche ℕ, è formato dagli interi positivi: 1, 2, 3, 4… e così via. Questo insieme è rappresentato dalla seguente notazione: ℕ = {1, 2, 3, 4, 5…}. Possono però essere rappresentati anche in modo più grafico, posizionandoli sulla linea dei numeri .
Questo secondo metodo prevede di tracciare una linea retta orizzontale e di scrivere lungo la linea i valori dei numeri naturali in modo ordinato. Quindi puoi facilmente visualizzare l’ ordine dell’insieme , questo sistema è molto utile per coloro che imparano questo insieme numerico. Nell’immagine seguente puoi vedere come sarebbe il layout della riga.
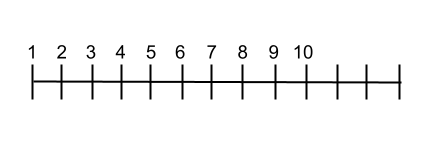
Operazioni con i numeri naturali
Ora che conosci tutte le caratteristiche e le proprietà dell’insieme ℕ, è il momento di applicarle alle operazioni aritmetiche , che sono l’applicazione principale di questi numeri. Successivamente, spiegheremo in dettaglio le quattro operazioni fondamentali (addizione, sottrazione, moltiplicazione e divisione).
Quando aggiungiamo valori naturali, otteniamo un altro numero ℕ: 3 + 6 = 9 . Ma quando sottraiamo tra numeri naturali, il risultato può essere un numero positivo o negativo. Queste ultime non appartengono all’insieme di cui stiamo parlando, quindi fanno parte dell’insieme ℕ solo le sottrazioni che hanno esito positivo: 4 – 2 = 2 .
Il caso della moltiplicazione tra numeri naturali è identico a quello dell’addizione, poiché possono dare come risultato solo un numero positivo. Ad esempio, se vogliamo moltiplicare 3 e 8, otteniamo 3 · 8 = 24 . Ma se dividiamo tra i numeri dell’insieme ℕ, in certi casi possiamo ottenere un numero decimale . In questa situazione, il risultato non fa parte del tutto naturale.
Pertanto, nell’insieme dei numeri naturali, sono definite solo l’addizione e la moltiplicazione. Queste due operazioni verificano le proprietà commutative e associative . Pertanto, se i numeri iniziali sono naturali, il risultato sarà sempre un numero naturale. In questo modo sono operazioni che rispettano sempre le proprietà dell’insieme ℕ.
Applicazioni dei numeri naturali
I numeri naturali sono spesso usati nella vita di tutti i giorni . Ad esempio, possono essere utilizzati per misurare la lunghezza di un tavolo o il tempo impiegato da una persona per raggiungere un negozio. Possono anche essere utilizzati per eseguire calcoli matematici, come addizioni o sottrazioni. I numeri interi possono essere utilizzati anche per determinare la posizione degli oggetti in uno spazio, ad esempio per posizionare i libri su uno scaffale.