La notazione matematica è un modo di comunicare idee e calcoli attraverso l’uso di simboli. Anche se a prima vista può sembrare confuso, con un po’ di pratica riuscirai a interpretarlo facilmente. In questo articolo ti mostreremo il significato di tutti i simboli utilizzati in questa notazione e alcuni esempi di come applicarli.
Cos’è la notazione matematica?
La notazione matematica è un modo di scrivere valori ed espressioni utilizzati in matematica. Questa tecnica consente ai matematici di esprimere le idee in modo conciso e preciso . La notazione matematica consente inoltre a coloro che praticano o studiano matematica di comprendere meglio i concetti.
Il linguaggio della matematica non deve essere confuso con la notazione scientifica, che è un modo di scrivere valori numerici. La notazione matematica invece è più un insieme di simboli che permettono di scrivere espressioni complesse, proprio come una lingua. Torneremo su questo argomento più dettagliatamente in seguito.
Come leggere la notazione matematica?
Imparare a interpretare la notazione matematica è più facile di quanto sembri, devi solo imparare il significato di ogni simbolo e una volta fatto, sarai in grado di leggere qualsiasi cosa scritta in notazione matematica. È semplicissimo, anche se ovviamente richiede pratica e molto tempo di studio.
Le espressioni matematiche sono molto logiche e seguono sempre degli schemi, quindi basta memorizzare le regole e poi saprai come estrapolarle a qualsiasi situazione. Possiamo descrivere calcoli anche molto complessi, questa è la magia del linguaggio matematico, che permette di comunicare in maniera metodica messaggi molto elaborati.
Componenti della notazione matematica
La notazione matematica è composta da una serie di simboli che rappresentano numeri, operazioni e le relazioni tra loro. All’inizio questi simboli possono sembrare complicati, ma con un po’ di pratica e comprensione, interpretare la notazione matematica dovrebbe diventare un gioco da ragazzi.
Successivamente, spiegheremo in dettaglio i quattro tipi di elementi che si possono trovare nel linguaggio matematico. A partire dal più elementare per finire con il più complesso e astratto. E una volta terminata la spiegazione teorica, parleremo dei tipi di notazioni numeriche esistenti.
Numeri e insiemi di numeri
Innanzitutto dobbiamo definire i numeri matematici , è un concetto matematico che designa una quantità relativa a un’unità. Possiamo descrivere qualsiasi valore numerico, seguendo il sistema di numerazione decimale e combinando i seguenti simboli: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9.
Se ordiniamo i numeri in base a proprietà diverse, otteniamo diverse categorie di numeri, chiamate insiemi di numeri. E questi gruppi di valori hanno anche i propri simboli che li designano, nell’elenco seguente li presentiamo tutti con il nome del gruppo corrispondente:
- ℙ: numeri primi
- ℕ: numeri naturali
- ℤ: Intero
- ℚ: numeri razionali
- ℝ: Numeri reali
- 𝕀: numeri immaginari
- ℂ: numeri complessi
- ℍ: quaternioni
Questi simboli vengono generalmente utilizzati nei nostri calcoli per determinare un’ampia gamma di numeri, tutti in una volta. Se ad esempio abbiamo un’espressione che accetta di conseguenza molti valori, invece di scrivere i numeri uno per uno, ci sarà più semplice specificare tali valori tramite il simbolo corrispondente al loro gruppo numerico .
Operatori e quantificatori
Ora che abbiamo discusso dei numeri, che sono l’essenza della matematica, dobbiamo parlare di operatori e quantificatori . I primi sono tutti quei simboli che ci permettono di rappresentare un’operazione: addizione (+), sottrazione (-), moltiplicazione (x o ·), divisione (÷), tra gli altri.
Tuttavia, abbiamo anche altri due tipi di operatori, che sono gli operatori logici e gli operatori relazionali. La prima esprime congiunzione, disgiunzione e negazione. Ci aiutano a proporre operazioni logiche che, a differenza delle operazioni aritmetiche, non funzionano con i numeri, ma con proposizioni matematiche.
Mentre la seconda ci permette di stabilire equivalenze e relazioni tra valori o espressioni matematiche. Questi simboli possono essere utilizzati nei calcoli aritmetici (per ordinare i numeri), ma sono più importanti in algebra, quando abbiamo variabili (ne parleremo più avanti in due sezioni).
Nell’elenco seguente potete trovare la definizione di tutti gli operatori di cui abbiamo parlato finora:
| Simbolo | Definizione | Tipo |
| + | Aggiunta | operatore aritmetico |
| – | Sottrazione | operatore aritmetico |
| X, *, · | Moltiplicazione | operatore aritmetico |
| ÷ | Divisione | operatore aritmetico |
| x² | Potenziamento | operatore aritmetico |
| √ | depositare | operatore aritmetico |
| E | Congiunzione | operatore logico |
| O | Disgiunzione | operatore logico |
| NO | Rifiuto | operatore logico |
| = | Uguale a | operatore di relazione |
| > | Più grande di | operatore di relazione |
| < | Più piccolo di | operatore di relazione |
| >= | Migliore o uguale | operatore di relazione |
| <= | minore o uguale a | operatore di relazione |
| ≠ | non è uguale a | operatore di relazione |
| ≡ | Esattamente la stessa | operatore di relazione |
| ≈ | quasi uguale | operatore di relazione |
| ≃ | Equivalente a | operatore di relazione |
| ∝ | Proporzionale | operatore di relazione |
Sebbene ci siano anche altri cinque operatori logici, che vengono utilizzati per spiegare la logica matematica dalla teoria degli insiemi. Che è un ramo che applica la logica degli insiemi , che viene utilizzata nel calcolo, nella geometria, nella statistica… Poi, ti mostriamo i simboli utilizzati e la loro definizione.
| Simbolo | Definizione |
| x∈A | x appartiene ad A |
| x ∉ A | x non appartiene ad A |
| ∪ | unione |
| ∩ | Intersezione |
| ⊂ | Inclusione |
Per quanto riguarda i quantificatori, possiamo definirli come simboli che indicano il numero di elementi di un insieme che soddisfano una determinata condizione (equivalenza, ordine, appartenenza, ecc.). Esiste un’ampia varietà di operatori, ma tra i più utilizzati possiamo evidenziare:
| Simbolo | Definizione | Tipo |
| ∀x | per tutti gli x | quantificare |
| ∃x | C’è almeno una x | quantificare |
| ∄x | non c’è x | quantificare |
| ∃!x | C’è solo una x | quantificare |
| | | Ad esempio | quantificare |
| ∴ | COSÌ | quantificare |
Espressioni matematiche e loro relazioni
Con i simboli che abbiamo trattato finora puoi capire molta matematica, ma non abbiamo ancora spiegato le loro applicazioni o relazioni in espressioni complesse, come operazioni combinate o calcoli algebrici. Inoltre, ci sono ancora simboli di relazione di cui discutere. Questi sono quelli che vedremo in questa sezione.
A partire dai simboli di raggruppamento, sono parentesi, parentesi quadre e parentesi graffe. Questi elementi sono essenziali nella designazione di formule complesse. La sua funzione principale è quella di dare priorità a determinati calcoli, all’interno di un’espressione globale. E ci sono diversi livelli di priorità tra i tre tipi. In questa espressione puoi vedere l’ordine di scrittura 3 {[2 + (3 – 2) · 2] – 4}.
| simboli | Definizione | Priorità |
| “(“E”)” | Parentesi | Priorità massima |
| “[“E”]” | Parentesi | seconda priorità |
| “{” E “}” | Chiavi | terza priorità |
E per finire questa categoria, parleremo di somme (Σ) e prodotti (∏) , che sono elementi che ci permettono di descrivere addizioni e moltiplicazioni ripetute. La somma equivale a dire: “somma di Xi, dove i prende i valori da 1 ad an”. E il prodotto è lo stesso, ma invece di aggiungere, moltiplichiamo.
analisi algebrica
La prima cosa di cui parlare riguardo ai simboli algebrici sono le variabili, che sono rappresentate dalle lettere dell’alfabeto. La loro funzione è imitare un numero , ma non hanno un valore fisso come le costanti matematiche , quindi possono assumere nuovi valori. Questo vale per equazioni, limiti, derivate, integrali, matrici…
Vogliamo infine parlare delle rappresentazioni di tutte queste operazioni algebriche di cui abbiamo appena parlato in quest’ultimo paragrafo. Da allora, costituiscono la base dell’algebra e bisogna sapere qual è la loro simbologia. Successivamente, ti mostriamo una tabella con i suoi diversi simboli e una breve definizione:
| Simbolo | Definizione |
| lim x → b | Limite (quando x tende verso b) |
| y’, ƒ’ (x), dy / dx | derivato |
| ∫ | Completare |
| A mxn | Matrice di dimensioni mxn |
Conclusione sui simboli del linguaggio matematico
Finora hai visto tutti i simboli importanti trattati in matematica, ovviamente ce ne sono altri di cui parlare. Ma queste sono più specifiche per ogni sottocategoria della matematica: geometria, statistica, algebra… Chiudiamo quindi questo argomento e parliamo di notazioni numeriche.
Tipi di notazioni numeriche
In questa sezione vedremo tutti i modi per esprimere i numeri matematici, poiché esistono diverse notazioni per farlo. All’inizio abbiamo menzionato il sistema decimale, che è il più utilizzato dai matematici. Successivamente, lo spiegheremo in modo più dettagliato e ti mostreremo altri tipi di notazione matematica:
notazione decimale
Il sistema numerico decimale è un sistema numerico posizionale (sistema in cui la posizione di ciascuna cifra ne determina il valore) si basa sui multipli e sottomultipli del numero 10. Poiché dieci è il numero utilizzato come base numerica . Pertanto, i dieci simboli numerici che utilizzeremo sono: 1, 2, 3, 4, 5, 6, 7, 8, 9 e 0.
Il valore di questi numeri è determinato dalla somma delle cifre moltiplicata per le potenze in base dieci, stabilite in base alla posizione . Ed è molto importante ricordare che per scrivere un numero inferiore a uno è necessario utilizzare il punto decimale. Di seguito è riportato un esempio:
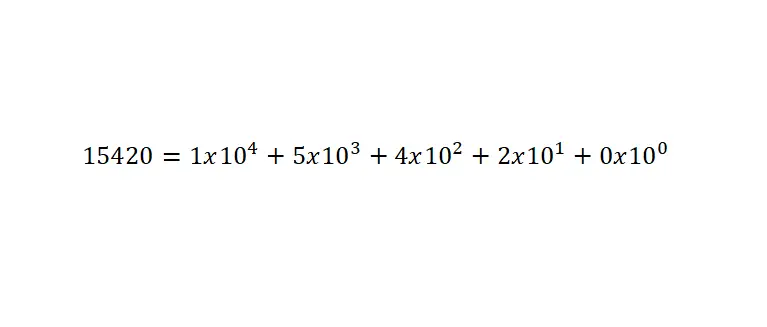
Notazione scientifica
La notazione in forma esponenziale o notazione scientifica è chiaramente uno dei tipi di scrittura più utilizzati nella scienza e nella tecnologia. In effetti, questo ci permette di esprimere numeri molto grandi e molto piccoli in modo semplice. Per comprendere la definizione di notazione scientifica, spiegheremo come passare un intero a questa notazione:
- Spostare la virgola decimale: devi spostare la virgola decimale tante volte quanto necessario fino a raggiungere la prima cifra (a sinistra se hai un numero molto grande e a destra se hai un numero molto piccolo).
- Stabilisci la base: scrivi quest’ultimo numero moltiplicato per dieci, quindi, accanto al valore che hai ottenuto spostando la virgola da un lato, devi scrivere una moltiplicazione per dieci: “x 10”.
- Aggiungi un esponente: con un valore pari al numero di volte in cui hai spostato la virgola decimale. Con numeri grandi lascerai l’esponente positivo, ma con numeri piccoli dovrai scriverlo con un segno negativo.
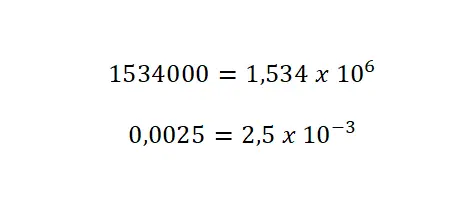
notazione esadecimale
Il sistema esadecimale si basa sul 16, il che significa che utilizza sedici simboli diversi: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E e F Come puoi vedi, questo sistema di numerazione è composto dai numeri del sistema decimale e da sei lettere. Questa notazione è generalmente utilizzata in particolare nell’IT e in tutto ciò che riguarda l’IT.
È importante chiarire che, avendo simboli in comune con altri tipi di notazione, bisogna sempre indicare che è scritta in esadecimale mediante la parentesi e l’indice 16 . Nell’esempio seguente puoi vedere da un esempio molto chiaro la conversione di un numero esadecimale in notazione decimale:
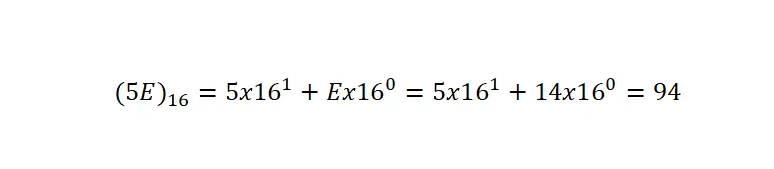
Per convertire un numero esadecimale in un’espressione decimale, dobbiamo scomporre il numero nelle moltiplicazioni della base, come abbiamo fatto nella notazione decimale, ma cambiando la base in 16 . Successivamente, moltiplicheremo ciascuna cifra per sedici, elevata alla posizione occupata da quella cifra specifica, meno uno.
notazione ottale
L’ultimo sistema di cui parleremo è la notazione ottale , che ha una base di 8. Ciò significa che utilizza solo otto simboli o numeri: 0, 1, 2, 3, 4, 5, 6 e 7. è il meno utilizzato sistema di numerazione di tutti quelli che abbiamo spiegato. È opportuno notare che le conversioni di questa notazione vengono effettuate secondo la stessa procedura delle precedenti.
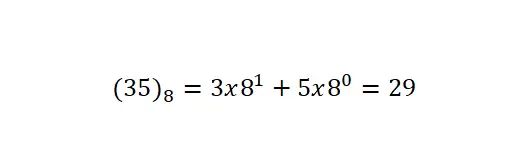
notazione nuova
Infine possiamo parlare del sistema numerico romano , oggi poco utilizzato, ma in passato molto importante nel campo della matematica. Poiché è stata una delle notazioni che ha dato vita alla matematica.
La tua scrittura è limitata a 7 simboli: I (1), V (5), X (10), L (50), C (100), D (500) e M (1000). E combinando queste lettere vengono scritti tutti i numeri. Se vuoi sapere come si combinano per dare origine ad altri numeri più grandi, ti consigliamo di leggere il nostro articolo su di loro, accedendo tramite l’ultimo link.
Come migliorare le prestazioni di lettura in notazione matematica?
Esistono diversi modi per migliorare le prestazioni nella lettura della notazione matematica. Un modo è leggere i simboli e i numeri ad alta voce. Un altro modo è familiarizzare con i simboli e il loro significato. Puoi anche esercitarti a leggere la notazione matematica utilizzando esercizi e problemi.
Speriamo di averti aiutato con questa guida, per favore, se hai domande, non esitare a scriverle nei commenti . Oppure, se desideri dare un contributo sull’argomento, speriamo di vederlo anche nei commenti. Detto questo, vi lasciamo un articolo su come imparare la matematica , nel caso voleste continuare a leggere.