Monomi - Mathority

Qui ti spieghiamo tutto quello che devi sapere sui monomi: cosa sono, quali sono le loro parti (e come identificarli), i diversi tipi di monomi, come calcolare le operazioni con i monomi, il valore numerico di un monomio. .. Inoltre, potrai vedere esempi ed esercizi risolti passo dopo passo di monomi.

Cosa sono i monomi?

In matematica, la definizione di monomio è la seguente:

Un monomio è un’espressione algebrica formata da una combinazione di numeri e lettere. Più precisamente un monomio è composto dal prodotto tra un numero e una o più variabili (lettere) elevate ad esponenti.

Ad esempio, il termine 7x ³ y ² è chiamato monomio perché ha un numero (7) e lettere diverse (x, y).

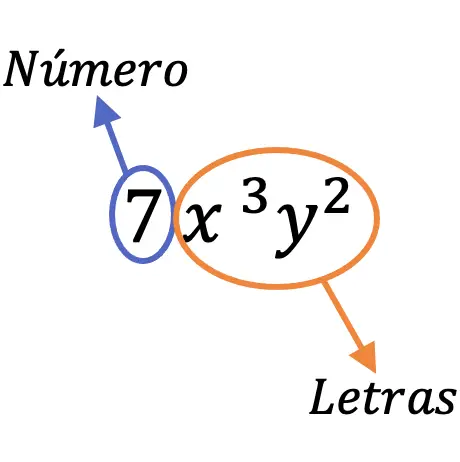
Parti di un monomio

Ora che abbiamo visto il significato di un monomio, vediamo quali sono tutte le parti di un monomio:

Coefficiente : è il numero che moltiplica le variabili (o lettere) del monomio.
Variabile : è ciascuna delle lettere che compaiono nel monomio.
Parte letterale : corrisponde a tutte le variabili che compongono il monomio con tutti i rispettivi esponenti.
Grado : è costituito dalla somma di tutti gli esponenti delle lettere che formano il monomio.

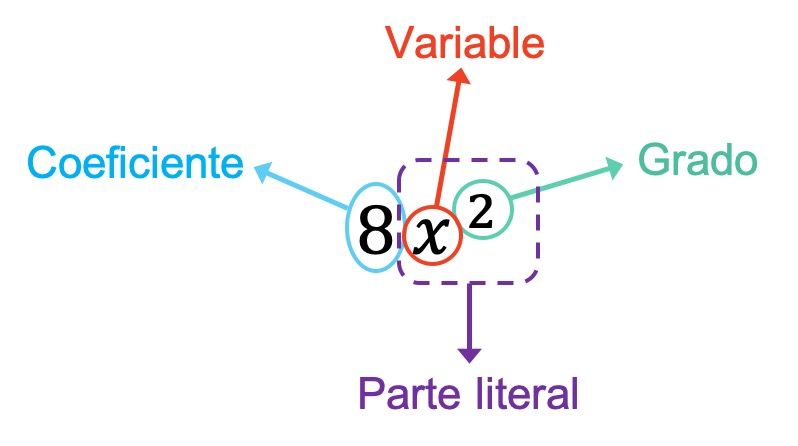
Il coefficiente del monomio nell’esempio sopra è 8 poiché è il numero che moltiplica le variabili. Anche in questo caso il monomio ha una sola variabile, ovvero x. Quindi, la parte letterale del monomio è formata da questa variabile più il suo esponente, che è x ² . Infine, il grado del monomio è 2 perché è l’unico esponente che possiede.

Prova ora a risolvere il seguente esercizio sulle parti di un monomio:

Individua tutte le parti del seguente monomio:

$5x^4y^2z$

vedi soluzione

Le componenti del monomio dell’enunciato sono:

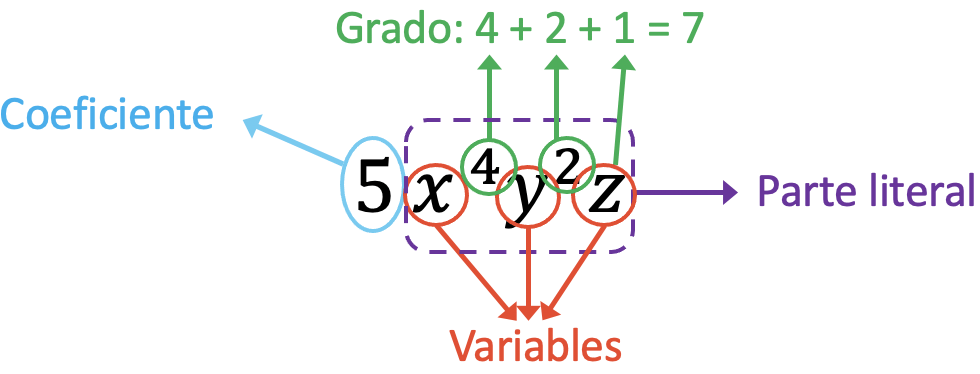
Il coefficiente del monomio nel problema è 5, poiché è il termine che moltiplica le lettere. D’altra parte, le variabili di questo monomio sono x, y, z. In terzo luogo, la parte letterale del monomio corrisponde all’espressione x ⁴ y ² z. E infine, il grado del monomio è uguale alla somma di tutti gli esponenti delle variabili, cioè 7 (4+2+1=7).

Nota che quando una lettera non ha esponente, in realtà significa che ha 1 come esponente. Pertanto, per calcolare il grado del monomio del problema, aggiungiamo un’unità che rappresenta l’esponente della variabile z.

Tipi di monomi

Esistono diversi tipi di monomi, ciascuno con le proprie proprietà. I monomi più importanti sono i monomi simili, i monomi omogenei, i monomi eterogenei e i monomi opposti. Successivamente vedremo le caratteristiche di ciascuna tipologia.

monomi simili

I monomi simili sono monomi che hanno la stessa parte letterale. Pertanto due o più monomi sono simili quando hanno le stesse lettere ed esponenti.

Ad esempio, i due monomi seguenti sono simili perché, pur avendo coefficienti diversi, sono formati dalle stesse variabili ed elevati agli stessi esponenti.

$4x^5y^3 \qquad \qquad 9x^5y^3$

Come vedremo in seguito, questa tipologia di monomi viene utilizzata per risolvere operazioni sui monomi.

monomi omogenei

Due monomi sono omogenei quando il loro grado assoluto è uguale.

Ad esempio, i seguenti due monomi sono omogenei perché il grado di entrambi è uguale a 5:

$2x^5 \qquad \qquad 6x^2y^3$

Il primo monomio ha una singola variabile elevata alla potenza di 5, quindi il suo grado è 5. E il secondo polinomio ha una variabile al quadrato e un’altra al cubo, quindi anche il suo grado è 5 (2+ 3 =5).

Come puoi vedere, affinché due monomi siano omogenei non è necessario che abbiano la stessa parte letterale, ma solo lo stesso grado assoluto.

monomi eterogenei

I monomi eterogenei sono monomi che non hanno lo stesso grado assoluto. In altre parole, i monomi eterogenei sono l’opposto dei monomi omogenei.

I seguenti 3 monomi sono eterogenei perché ciascuno ha un grado diverso:

$x^8 \qquad 3xy \qquad 7a^9b^2$

Il primo monomio è di grado 8, il secondo monomio è di grado 2 e il terzo monomio è di grado 11. Pertanto i tre monomi sono eterogenei tra loro.

Monomi opposti

I monomi opposti sono monomi omogenei (hanno la stessa parte letterale) e inoltre i loro coefficienti sono opposti, cioè i loro coefficienti hanno lo stesso valore ma segno opposto.

Ad esempio, i seguenti due monomi sono opposti:

$3x^5y^2 \qquad \qquad -3x^5y^2$

I due monomi precedenti sono opposti perché differiscono solo per il segno, il primo ha segno positivo e il secondo segno negativo.

Ora che hai visto diversi esempi di monomi, potresti essere interessato a un’altra espressione algebrica simile: il binomio . Infatti un binomio è formato dalla somma (o sottrazione) di più monomi, quindi è interessante vedere la relazione tra questi due concetti. Puoi vedere qual è il significato di binomio cliccando su questo link.

Operazioni con i monomi

Per approfondire il concetto di monomi, vedremo quali operazioni si possono fare con i monomi. In particolare i monomi possono essere sommati, sottratti, moltiplicati, divisi e potenti. E ogni tipo di operazione ha le sue peculiarità, quindi le analizzeremo una per una separatamente di seguito.

somma di monomi

Due o più monomi possono essere sommati solo se sono monomi simili. Allora la somma di due monomi simili è uguale ad un altro monomio composto dalla stessa parte letterale e dalla somma dei coefficienti di questi due monomi.

Esempi di somme di monomi

$2x^4+3x^4 = 5x^4$
$4y^2+y^2 = 5y^2$
$7x^3y+2x^3y = 9x^3y$
$2a^3b^2c^6+6a^3b^2c^6 = 8a^3b^2c^6$
$4x^3+2x^3+5x^3=6x^3+5x^3=11x^3$

Se vuoi esercitarti a fare esercizi di addizione monomiale, puoi cercarli nel motore di ricerca in alto a destra, perché abbiamo un’intera pagina piena di esercizi di addizione monomiale risolti.

sottrazione di monomi

Due o più monomi possono essere sottratti solo se sono monomi simili. Pertanto la sottrazione di due monomi simili è uguale ad un altro monomio composto dalla stessa parte letterale e dalla sottrazione dei coefficienti di questi due monomi.

Esempi di sottrazione di monomi

$7x^2-4x^2 = 3x^2$
$5y^3-y^3 = 4y^3$
$8x^6y-4x^6y = 4x^6y$
$10a^3b^4c^2-6a^3b^4c^2 = 4a^3b^4c^2$
$11x^3-4x^3-5x^3=7x^3-5x^3=2x^3$

Puoi esercitarti con gli esercizi di sottrazione monomiali risolti passo dopo passo che puoi trovare sul nostro sito web. Li puoi trovare tramite il motore di ricerca in alto a destra.

moltiplicazione di monomi

Il risultato della moltiplicazione di due monomi è un altro monomio il cui coefficiente è il prodotto dei coefficienti dei monomi e la cui parte letterale si ottiene moltiplicando le variabili che hanno la stessa base, cioè sommando i loro espositori.

Quindi, per risolvere il prodotto tra due monomi diversi, occorre moltiplicare tra loro i coefficienti e sommare gli esponenti delle potenze che hanno la stessa base.

Se invece moltiplichiamo due monomi con potenze di base diverse, dobbiamo semplicemente moltiplicare tra loro i loro coefficienti e lasciare le stesse potenze:

$5x^2\cdot 3y^4 = (5\cdot 3) x^2y^4 = 15x^2y^4$

Esempi di moltiplicazione di monomi

$6x^4 \cdot 7x^5= (6\cdot 7)x^{4+5} = 42x^9$
$4y \cdot 2y^3 = (4\cdot 2)y^{1+3} = 8 y^4$
$5x^2y^4\cdot (-8x^8y^2)=(5\cdot (-8))x^{2+8}y^{4+2} = -40x^{10}y^6$
$-3x^6y^4 \cdot (-4x^2z)= (-3\cdot (-4)) x^{6+2}y^4z= 12x^8y^4z$
$-3x^8\cdot 4x^5\cdot (-x^2) =-12x^{13}\cdot (-x^2)= 12x^{15}$

Per esercitarti con gli esercizi passo passo risolti di moltiplicazione dei monomi, puoi consultare l’articolo che abbiamo su questo sito. Lo troverai facilmente con il motore di ricerca in alto a destra.

divisione dei monomi

Il risultato della divisione dei monomi è un altro monomio il cui coefficiente è equivalente al quoziente dei coefficienti dei monomi e la cui parte letterale si ottiene dividendo le variabili che hanno la stessa base, cioè sottraendo i loro espositori.

Quindi per dividere due monomi diversi basta dividere tra loro i coefficienti e sottrarre gli esponenti delle potenze che hanno la stessa base.

Esempi di divisione di monomi

$7x^6 : 7x^4= (7:7)x^{6-4} = 1x^2=x^2$
$12y^5 : 4y^2= (12:4)y^{5-2} = 3y^3$
$15x^7y^6 :3x^4y^5= (15:3)x^{7-4}y^{6-5} = 5x^3y$
$27x^9y^7 :(-3x^5y^2)= (27:(-3))x^{9-5}y^{7-2}= -9x^4y^5$
$-18x^{13} : 3x^4 : (-2x^7) = -6x^9: (-2x^7) = 3x^2$

La divisione dei monomi è più difficile di quanto sembri, quindi ti consigliamo di provare a svolgere passo dopo passo gli esercizi risolti che abbiamo sulla divisione dei monomi . Il modo più veloce per trovarli è tramite il nostro motore di ricerca in alto a destra.

potenza di un monomio

Per calcolare la potenza di un monomio occorre elevare ogni elemento del monomio all’esponente potenza . In altre parole, la potenza di un monomio consiste nell’elevare il suo coefficiente e le sue variabili (lettere) all’esponente della potenza.

Ricorda dalle proprietà delle potenze che quando eleviamo un termine già elevato, i due esponenti vengono moltiplicati tra loro. Per questo motivo , nella potenza di un monomio, l’esponente di ciascuna lettera va sempre moltiplicato per l’esponente che indica la potenza .

Esempi di potenze di monomi

$\left(5x^6\right)^2 = 5^2\left(x^6\right)^2 = 5^2x^{6\cdot 2} = 25x^{12}$
$\left(2x^5\right)^4 = 2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = 16x^{20}$
$\left(-4y^3\right)^2 = (-4)^2\left(y^3\right)^2 = (-4)^2y^{3\cdot 2} = 16y^{6}$
$\left(3x^4y\right)^3 = 3^3\left(x^4y\right)^3 = 3^3x^{4\cdot 3}y^{1\cdot 3} = 27x^{12}y^3$
$\left(-2a^5b^7\right)^3 = (-2)^3\left(a^5b^7\right)^3 = (-2)^3a^{5\cdot 3}b^{7\cdot 3} = -8a^{15}b^{21}$

È abbastanza facile commettere errori in questo tipo di operazioni con i monomi. Ecco perché ti consigliamo di esercitarti con gli esercizi che abbiamo risolto passo dopo passo sul nostro sito web. Li troverai velocemente cercandoli nel motore di ricerca in alto a destra.

Valore numerico di un monomio

Il valore numerico di un monomio è il risultato ottenuto sostituendo alle variabili di un monomio determinati valori.

Ad esempio, se abbiamo il seguente monomio:

$5x^2$

Se vogliamo trovare il valore numerico del monomio precedente per

$x=2$

è necessario sostituire la lettera

$x$

del monomio per 2 e risolvi le operazioni risultanti:

$5\cdot 2^2= 5 \cdot 4 = 20$

Quindi il valore numerico del monomio

$5x^2$

Per

$x=2$

è uguale a 20.

È inoltre possibile determinare il valore numerico di una multivariabile monomiale. Ad esempio, se abbiamo la seguente bivariabile, o in altre parole, due variabili, monomiale:

$3x^4y$

Per calcolare il valore numerico del monomio di cui sopra quando

$x$

vale 1 e

$y$

è -2, sostituiamo le lettere con i rispettivi valori:

$3\cdot 1^4\cdot (-2)= 3 \cdot 1 \cdot (-2) = -6$

Quindi il valore numerico del monomio del problema per

$x=1$

$y=-2$

restituisce -6.

Monomi e polinomi

Infine, sappi che i polinomi possono essere formati da monomi:

Un polinomio è il raggruppamento di due o più monomi.

$P(x)= 4x^5+3x^2-7x$

Ad esempio, il polinomio precedente risulta dalla somma (o sottrazione) di 3 monomi eterogenei.

Per curiosità, quando un polinomio ha solo 2 monomi, si chiama binomio . E quando un polinomio ha esattamente 3 monomi, si chiama trinomio .

Se vuoi saperne di più sui polinomi, puoi visitare la pagina principale del web, dove spieghiamo tutto ciò che devi sapere sui polinomi.